В) Оценки вероятностных гистограмм.
Рассмотрим, как оценивается плотность распределения по отдельной дискретной реализации 
стационарной случайной последовательности. Вероятность того, что ордината примет некоторое значение в интервале 
в серии из 
испытаний, можно оценить выражением
где 
- число попаданий в 
- й интервал; - общее число измерений.
Полученная частота 
стремится к истинной вероятности при 
.
Точность оценки определяется средним значением квадрата ошибки
.
Здесь величина 
представляет собой дисперсию оценки:
;
а 
- смещение оценки:
.
Смещение оценки (систематическая ошибка) может быть определена по формуле [22]: 
, где 
- вторая производная функции 
по аргументу 
. Дисперсия оценки в общем виде имеет форму:
,
где 
- постоянная.
Дадим формальное описание метода. Интервал изменения величины 
делят на 
подынтервалов равной длины (их называют интервалами группировки), при этом вся область значений распадается на 
интервалов. После этого, перебирая данные, фиксируют число попаданий на каждый интервал. Итак, зная величину интервала 
и число разрядов , положим 
и 
, где 
- верхняя граница текущего интервала; - длина интервала группировки.
Очевидно, что 
и 
. Теперь нужно определить, какому интервалу принадлежит число. Это легко программируется, но сортировка получается длинной и медленной. Самый быстрый метод заключается в определении значения целой переменной 
, соответствующей номеру интервала группировки, которому принадлежит число. Таким образом, чтобы подсчитать число элементов в каждом интервале группировки, можно действовать следующим образом: получить число, вычислить , как 
, установить 
, где 
- массив из элементов, а каждый элемент служит счётчиком для класса . Блок-схема алгоритма представлена на рис. 1.13.
|
Основная трудность заключается в определении интервала . Для этого в целом ряде случаев могут быть использованы формулы [2]: 
или 
, где - число интервалов группировки; - объём выборки или число испытаний.
Рис. 1.13
г) Оценки спектральной плотности.
Спектральная плотность стационарного случайного процесса описывает точную частотную структуру процесса как энергию сигнала (или мощность), приходящуюся на единицу полосы частот. Среднее значение квадрата значений реализации (мощность) в интервале частот можно получить, подавая эту реализацию на вход полосового фильтра с узкой полосой пропускания и осредняя возведённую в квадрат функцию на выходе фильтра. Это осреднённое значение квадрата приближается к точному его значению при 
:
,
где 
- составляющие функции 
, имеющие частоты в интервале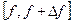 
.
При малых значениях 
спектральную плотность можно определить, пользуясь приближённым равенством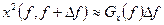 
или более строго
(1.62)
Откуда следует, что 
- всегда действительная неотрицательная функция.
Спектральная плотность с автокорреляционной функцией связана преобразованием Фурье
.
Переход к последнему выражению возможен потому, что 
есть чётная функция аргумента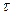 
.
во всей области частот от 
до 
. Эти функции более удобны для математических выкладок. Физически осуществимые функции связаны с функциями 
Рассматриваемые функции спектральной плотности называются физически осуществимыми, в отличии от двухсторонних спектральных плотностей , определённых следующим образом (рис. 1.14):
|
Рис. 1.14
Спектральная плотность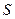 
связана с корреляционной функцией взаимным преобразованием Фурье:
(1.63)
Существуют три классические схемы вычисления оценок спектральной плотности: метод прямой фильтрации, непосредственное преобразование Фурье и преобразование Фурье корреляционной функции.
Метод прямой фильтрации впрямую реализует определение спектральной плотности в форме (1.62). Схема вычислителя (рис. 1.15) содержит настраиваемый узкополосный фильтр с центральной частотой 
и шириной полосы 
(обозначен на рис. 18 – Ф) и блок, вычисляющий среднее значение квадрата отфильтрованного сигнала 
, так что оценка получается по формуле
(1.64)
|
где 
- оценка спектральной плотности; 
- полоса пропускания фильтра; - центральная частота фильтра; 
- время осреднения; 
- отфильтрованный сигнал.
Рис. 1.15
Точность оценки определяется средним квадратом ошибки по формуле
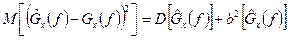, где
- дисперсия оценки;
- смещение оценки.
Таким образом, оценка спектральной плотности является несостоятельной и может иметь смещение в пределах интервала дискретизации по частоте. Эти свойства затрудняют её использование и требуют применения дополнительной обработки результатов в виде сглаживания.
Рассмотренный способ применяется при аппаратурной реализации вычислений, т.е. при создании специальных приборов, вычисляющих оценки спектральной плотности в отдельных частотных диапазонах; помимо этого, метод прямой фильтрации может быть реализован на ЦВМ; в этом случае выполняется цифровая реализация полосопропускающего фильтра.
При втором методе вычисления оценок спектральной плотности – методе непосредственного преобразования Фурье – производится вычисление преобразования Фурье исходной реализации:
,
затем вычисляются оценки спектральной плотности в частной области:
.
И, наконец, третий метод получения оценок спектральной плотности связан с предварительным вычислением корреляционной функции, а затем, по формулам (1.63) и (1.64) и оценкой спектральной плотности. Можно показать, что все три описанных метода эквивалентны [17]. В общем случае классические методы спектрального анализа можно свести к следующим процедурам: оценка корреляционной функции; вычисление спектральной плотности.
В виде практической цифровой процедуры этот способ был впервые реализован Блекманом и Тьюки [14]. Рассмотрим этот алгоритм.
Для последовательности 
из величин вычисляются значения корреляционной функции по формуле
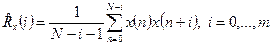
где предполагается, что значения 
центрированы, т.е., если среднее значение не равно нулю, его сначала вычисляют и затем вычитают из всех значений данных.
Значения спектральной плотности для различных частот вычисляются посредством интегрирования выражения (1.63) методом трапеций по формуле
(1.65)
где 
- интервал времени между отсчётами; 
- оценка спектральной плотности на частоте 
, так называемая «первичная оценка»; 
- оценка корреляционной функции при шаге 
; 
- максимальное число шагов; 
- граничная частота.
Определяемую по формуле (1.65) функцию называют периодограммой. Если брать только дискретные частоты 
, то будет получено 
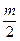независимых оценок спектральной плотности, поскольку оценки, стоящие друг от друга менее чем на интервал корреляции 
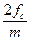, будут коррелированны. Для этих дискретных частот формула (1.65) упрощается:
Здесь индекс 
называется порядком гармоники.
При проверке должно вычисляться среднее значение квадрата реализации в диапазоне частот 
в соответствии с определением спектральной плотности (1.62), т.е. 
, или в дискретном виде
.
Поскольку оценки нуждаются в сглаживании, применяется взвешивание как во временной, так и в частотной области. Самым наглядным способом является применение временного окна
что в частотной области соответствует следующей процедуре:
