Глава 4. Ряды
Ряды с комплексными членами
Рассмотрим последовательность комплексных чисел  , n = 1,2,…
, n = 1,2,…
Определение 45. Последовательность комплексных чисел 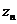 называется сходящейся, а число
называется сходящейся, а число  ее пределом
ее пределом  , если существуют конечные пределы
, если существуют конечные пределы 

Определение 46. Числовым рядом с комплексными членами называется составленное из последовательности комплексных чисел выражение:  .
.
Частичной суммой ряда называнется выражение  .
.
Определение 47. Ряд  называется сходящимся, если существует конечное число S такое, что
называется сходящимся, если существует конечное число S такое, что  , где S – сумма ряда.
, где S – сумма ряда.
Так как S – комплексное число, то S = u + iv.
Необходимое и достаточное условие сходимости: ряд  сходится к сумме S = u + iv тогда и только тогда, когда сходятся в отдельности ряды из действительных и мнимых частей его членов и выполняются равенства:
сходится к сумме S = u + iv тогда и только тогда, когда сходятся в отдельности ряды из действительных и мнимых частей его членов и выполняются равенства: 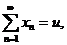
 .
.
Определение 48. Ряд  называется абсолютно сходящимся, если сходится ряд из модулей членов данного ряда
называется абсолютно сходящимся, если сходится ряд из модулей членов данного ряда 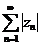 .
.
Замечание. Для рядов с комплексными членами справедливы все признаки сходимости и абсолютной сходимости, сформулированные ранее для рядов с действительными членами. Это необходимый признак и достаточные признаки: сравнения и предельного сравнения, Даламбера, интегральный и радикальный признаки Коши.
Теорема 14. Если существует сходящийся ряд с положительными членами  такой, что для всех
такой, что для всех 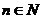 справедливо неравенство
справедливо неравенство  , то ряд
, то ряд  сходится и притом абсолютно.
сходится и притом абсолютно.
Пример 1. Исследовать на абсолютную сходимость ряд  . (*)
. (*)
Решение.
Рассмотрим ряд из модулей:
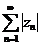 =
= 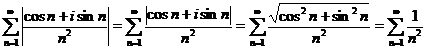 – сходящийся числовой ряд. Следовательно, ряд (*) сходится абсолютно.
– сходящийся числовой ряд. Следовательно, ряд (*) сходится абсолютно.
Пример 2. Исследовать на абсолютную сходимость ряд  . (**)
. (**)
Решение.
Исследуем на сходимость ряд из абсолютных величин с помощью радикального признака Коши:

 ряд из модулей сходится, следовательно, ряд (**) сходится абсолютно.
ряд из модулей сходится, следовательно, ряд (**) сходится абсолютно.
Степенные ряды
Основные понятия
Определение 49. Пусть функции fn (z), 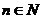 , определены и непрерывны в одной и той же области D. Выражение
, определены и непрерывны в одной и той же области D. Выражение 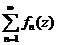 называется функциональным рядом.
называется функциональным рядом.
Для каждой точки z = z 0 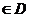 функциональный ряд
функциональный ряд 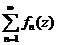 обращается в числовой ряд:
обращается в числовой ряд:  .
.
Определение 50. Если в данной точке z 0 числовой ряд сходится, то говорят, что функциональный ряд также сходится в точке z 0, а сама точка называется точкой сходимости функционального ряда.
Множество всех точек сходимости называется областью сходимости. Функциональный ряд 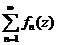 называется сходящимся в области D 1.
называется сходящимся в области D 1.
Определение 51. Функциональный ряд 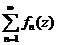 называется абсолютно сходящимся в области D 1, если в этой области сходится ряд из абсолютных величин членов данного ряда.
называется абсолютно сходящимся в области D 1, если в этой области сходится ряд из абсолютных величин членов данного ряда.
Определение 52. Сходящийся в области D 1 функциональный ряд 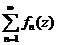 называется равномерно сходящимся в этой области, если для любого положительного числа ε найдется номер N = N (ε) такой, что для остатка ряда
называется равномерно сходящимся в этой области, если для любого положительного числа ε найдется номер N = N (ε) такой, что для остатка ряда  при всех
при всех 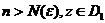 имеет место оценка
имеет место оценка  .
.
Критерий Вейерштрасса (критерий равномерной сходимости).
Пусть функциональный ряд 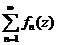 сходится в области D 1, и пусть существует сходящийся знакоположительный числовой ряд
сходится в области D 1, и пусть существует сходящийся знакоположительный числовой ряд  такой, что для всех
такой, что для всех  члены функционального ряда удовлетворяют условию
члены функционального ряда удовлетворяют условию  , тогда функциональный ряд сходится абсолютно и равномерно в области D 1, а числовой ряд
, тогда функциональный ряд сходится абсолютно и равномерно в области D 1, а числовой ряд  называется мажорирующим, или мажорантой.
называется мажорирующим, или мажорантой.
Определение 53. Функциональный ряд  называется степенным по степеням (z – z 0). Функциональный ряд
называется степенным по степеням (z – z 0). Функциональный ряд  называется степенным по степеням z.
называется степенным по степеням z.
Теорема 15 (теорема Абеля). Если степенной ряд  сходится в точке
сходится в точке  , то он абсолютно сходится для всех z таких, что
, то он абсолютно сходится для всех z таких, что  , причем сходимость будет равномерной в любом замкнутом круге
, причем сходимость будет равномерной в любом замкнутом круге  Если же ряд
Если же ряд  расходится в точке
расходится в точке 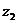 , то он расходится и для всех z таких, что
, то он расходится и для всех z таких, что 
На границе круга сходимости ряд может как сходиться, так и расходиться.
Радиус сходимости R может быть найден либо при помощи признака Даламбера, либо радикального признака Коши:
 или
или  .
.
Сходящийся ряд  сходится в круге с центром в точке О:
сходится в круге с центром в точке О:  , а степенной ряд
, а степенной ряд  – в круге с центром в точке z 0 :
– в круге с центром в точке z 0 :  .
.
Теорема 16. В круге сходимости  степенного ряда
степенного ряда  его сумма f (z) является аналитической функцией.
его сумма f (z) является аналитической функцией.
Пример 3. Найти радиус сходимости степенного ряда 
Решение.
Для решения воспользуемся радикальным признакым признаком Коши:

Пример 4. Найтиобласть абсолютной сходимости и область равномерной сходимости ряда  .
.
Решение.
Для нахождения области сходимости применим признак Даламбера:


 , отсюда
, отсюда
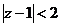 , следовательно, ряд сходится в круге с центром в точке z 0 = 1 и радиусом R = 2.
, следовательно, ряд сходится в круге с центром в точке z 0 = 1 и радиусом R = 2.
Исследуем на сходимость на границе круга, т.е. на окружности  .
.
Подставим данное выражение в ряд из модулей  . Получим
. Получим

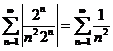 – сходящийся числовой ряд. Следовательно, ряд из модулей сходится, и это означает, что исходный ряд сходится и на границе круга, т.е. сходится абсолютно в замкнутом круге
– сходящийся числовой ряд. Следовательно, ряд из модулей сходится, и это означает, что исходный ряд сходится и на границе круга, т.е. сходится абсолютно в замкнутом круге  .
.
Проверим на равномерную сходимость при помощи признака Вейерштрасса.

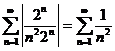 – сходящийся ряд мажоранта, следовательно, исходный ряд сходится равномерно в замкнутом круге
– сходящийся ряд мажоранта, следовательно, исходный ряд сходится равномерно в замкнутом круге  .
.
Исходный ряд сходится абсолютно и равномерно в замкнутом круге  .
.
Ряды Тейлора и Маклорена
Определение 54. Пусть дана функция f (z), аналитическая в некоторой окрестности точки z 0. Ряд 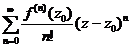 называется рядом Тейлора функции f (z) и внутри круга сходимости выполняется равенство:
называется рядом Тейлора функции f (z) и внутри круга сходимости выполняется равенство:
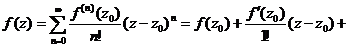

 . (25)
. (25)
Теорема 17 (теорема Тейлора). Всякая аналитическая функция f (z) внутри круга с центром в точке z 0 и радиусом R, т.е  , может быть разложена внутри этого круга в степенной ряд Тейлора по степеням (z – z 0):
, может быть разложена внутри этого круга в степенной ряд Тейлора по степеням (z – z 0):  , коэффициенты cn которого определяются по формулам:
, коэффициенты cn которого определяются по формулам:
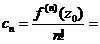 (по интегральной формуле Коши (21)) =
(по интегральной формуле Коши (21)) = 
где Г – какая-нибудь фиксированная концентрическая окружность радиуса r < R, т.е. лежащая внутри круга сходимости.
Замечание.  М – число:
М – число:  .
.
При z 0 = 0 ряд Тейлора называется рядом Маклорена.
При решении многих задач рекомендуется пользоваться следующими разложениями в ряд Маклорена элементарных функций:
Таблица разложения в ряд Маклорена основных элементарных функций
1. 
 ,
, 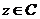 .
.
2. 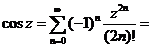
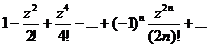 ,
, 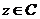 .
.
3. 
 ,
, 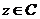 .
.
4. 
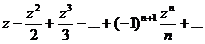 ,
,  – область сходимости.
– область сходимости.
5. 
 ,
,  – область сходимости.
– область сходимости.
6. 

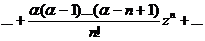 ,
,  – область сходимости,
– область сходимости, 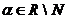 .
.
В случае, когда  функция
функция  раскладывается по биному Ньютона в многочлен, причем разложение имеет место во всей плоскости.
раскладывается по биному Ньютона в многочлен, причем разложение имеет место во всей плоскости.
При 
 ,
,  – область сходимости.
– область сходимости.
7.  ,
,  – область сходимости.
– область сходимости.
Пример 5. Разложить  в ряд Тейлора по степеням (z +3).
в ряд Тейлора по степеням (z +3).
Решение.


Ряд Лорана
Рядом, обобщающим понятие степенного ряда, является ряд Лорана.
Рассмотрим разложение в ряды двух функций:
1-ый ряд: 
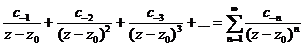 (26)
(26)
2-ой ряд:  (27)
(27)
Область сходимости ряда (26), если она существует, определяется неравенством:
 , отсюда,
, отсюда,  , где
, где  (*)
(*)
Область сходимости ряда (27), если она существует, определяется неравенством:
 , отсюда,
, отсюда,  , где
, где 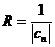 (**),
(**),
причем 
Определение 55. Рядом Лорана называется ряд  , представляющий собой сумму двух рядов:
, представляющий собой сумму двух рядов:

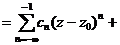
 , (28)
, (28)
при этом ряд (26) –  – называется главной частью, а ряд (27) –
– называется главной частью, а ряд (27) –  – правильной частью ряда Лорана.
– правильной частью ряда Лорана.
Лемма. Ряд (26) называется сходящимся в точке z тогда и только тогда, когда оба ряда (26) и (27) сходятся в этой точке.
Ряд  сумма ряда Лорана.
сумма ряда Лорана.
 Из (*) и (**) следует, что при условии
Из (*) и (**) следует, что при условии 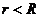 областью сходимости ряда Лорана (28), полученного сложением рядов (26) и (27), служит кольцо
областью сходимости ряда Лорана (28), полученного сложением рядов (26) и (27), служит кольцо  , ограниченное концентрическими окружностями с центром в точке
, ограниченное концентрическими окружностями с центром в точке  и радиусами r и R (рис. 42).
и радиусами r и R (рис. 42).
Теорема 18. В кольце сходимости сумма ряда Лорана f (z) представляет собой однозначную аналитическую функцию.
Теорема 19. Если f (z) – сумма ряда Лорана, то коэффициенты cn можно вычислить по формуле
 , (29)
, (29)
где Г – концентрическая окружность 
 , лежащая внутри кольца сходимости.
, лежащая внутри кольца сходимости.
Замечание. Практически формула (29) почти никогда не используется для нахождения коэффициентов ряда Лорана. Из теоремы Тейлора видим, что эта же формула используется для вычисления коэффициентов ряда Тейлора. Можно сделать вывод, что обычно разложение конкретной функции в ряд Лорана тем или иным способом сводится к разложению ее в ряд Тейлора (25).
Теорема 20 (теорема Лорана). Каждая однозначная аналитическая в кольце D:  функция f (z) представляется в этом кольце сходящимся рядом Лорана
функция f (z) представляется в этом кольце сходящимся рядом Лорана  .
.
Следствие 1. Кольцо D может быть вырожденным, т.е. либо  , либо
, либо  , либо
, либо  и
и  .
.
Следствие 2. Рядом Лорана для функции f (z) в окрестности бесконечно удаленной точки  называется ряд
называется ряд  , сходящийся в некотором кольце
, сходящийся в некотором кольце  . При этом главной частью ряда Лорана является ряд
. При этом главной частью ряда Лорана является ряд  , а правильной – ряд
, а правильной – ряд  . Функция f (z) предполагается аналитической в области
. Функция f (z) предполагается аналитической в области  за исключением, быть может, точки
за исключением, быть может, точки  .
.
Пусть  , тогда рядом Лорана для функции f (z) в окрестности бесконечно удаленной точки
, тогда рядом Лорана для функции f (z) в окрестности бесконечно удаленной точки  называется ряд
называется ряд  , сходящийся в некотором кольце
, сходящийся в некотором кольце  . Функция f (z) предполагается аналитической в области
. Функция f (z) предполагается аналитической в области 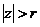 за исключением, быть может, точки
за исключением, быть может, точки  . В этом случае выполним преобразование
. В этом случае выполним преобразование 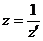 , тогда изучение функции f (z) сведется к изучению функции
, тогда изучение функции f (z) сведется к изучению функции  , аналитической в круге
, аналитической в круге  за исключением, быть может, точки
за исключением, быть может, точки  .
.
 Следствие 3. Пусть функция f (z) аналитична в многосвязной области D, ограниченной контуром Г и внутренними контурами
Следствие 3. Пусть функция f (z) аналитична в многосвязной области D, ограниченной контуром Г и внутренними контурами  (рис. 43). Если точка
(рис. 43). Если точка  лежит внутри или на границе одного из внутренних контуров
лежит внутри или на границе одного из внутренних контуров  , i = 1,…, m и величина
, i = 1,…, m и величина  меньше расстояния R от точки
меньше расстояния R от точки  до остальной части границы области D или до точки, в которой f (z) не аналитична, т.е.
до остальной части границы области D или до точки, в которой f (z) не аналитична, т.е. 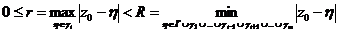 , то в кольце
, то в кольце  функция f (z) может быть представлена ее рядом Лорана.
функция f (z) может быть представлена ее рядом Лорана.
Пример 6. Разложить в ряд Лорана по степеням z функцию  : 1) в окрестности точки
: 1) в окрестности точки  , 2) в окрестности бесконечно удаленной точки
, 2) в окрестности бесконечно удаленной точки  .
.
Решение.
1) Найдем разложение в ряд Лорана в точке  по степеням z, т.е.
по степеням z, т.е.  .
.
Известно разложение в ряд Маклорена функции  :
: 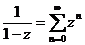 , где
, где  – область сходимости. Следовательно, разложение в ряд Маклорена функции
– область сходимости. Следовательно, разложение в ряд Маклорена функции  будет иметь вид:
будет иметь вид:  , область сходимости
, область сходимости 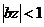

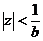 .
.
Представим функцию  в виде
в виде  :
:
 – искомый ряд Лорана.
– искомый ряд Лорана.
Ряд начинается с n = 0, т.е. разложение содержит только правильную часть.
Область сходимости ряда:  , т.е.
, т.е.  – круг с центром в точке
– круг с центром в точке  и радиусом
и радиусом  .
.
2) Найдем разложение в ряд Лорана в точке  по степеням z, т.е.
по степеням z, т.е.  .
.
По следствию 2 к теореме Лорана для этого требуется представить функцию в виде:
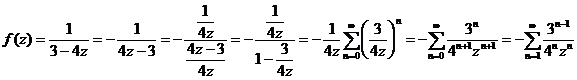 – ряд Лорана. Заметим, что ряд содержит только правильную часть.
– ряд Лорана. Заметим, что ряд содержит только правильную часть.
При 
 . Следовательно, для сходимости полученного ряда должно выполняться неравенство
. Следовательно, для сходимости полученного ряда должно выполняться неравенство  . Тогда областью сходимости ряда является область вне круга:
. Тогда областью сходимости ряда является область вне круга:  .
.
Пример 7. Разложить в ряд Лорана по степеням z функцию  .
.
 Решение.
Решение.
Так как функцию требуется разложить в ряд Лорана по степеням z, то  , и, следовательно, нас интересуют кольцевые области аналитичности функции f (z) с центром в точке
, и, следовательно, нас интересуют кольцевые области аналитичности функции f (z) с центром в точке  . Так как знаменатель обращается в нуль в точках
. Так как знаменатель обращается в нуль в точках 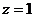 и
и  , то это области: D 1:
, то это области: D 1:  ; D 2:
; D 2:  ; D 3:
; D 3:  (рис. 44).
(рис. 44).
Разложим данную функцию на элементарные дроби:




При z: 
 А = – В
А = – В
При z 0: 1 = –2 А – В
Отсюда, 1 = 2 В – В  В = 1, А = –1.
В = 1, А = –1.

Рассмотрим отдельно каждое слагаемое и найдем их разложения в ряды в областях D 1, D 2, D 3.
1) 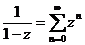 – известное разложение в ряд Маклорена (№7), область сходимости
– известное разложение в ряд Маклорена (№7), область сходимости  .
.
2) Представим функцию  в виде
в виде  , т.е. сведем к известному разложению в ряд Маклорена (№7):
, т.е. сведем к известному разложению в ряд Маклорена (№7):
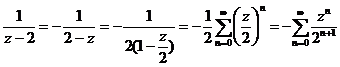 , область сходимости
, область сходимости 

 .
.
3)  , область сходимости
, область сходимости 

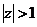 .
.
4)  , область сходимости
, область сходимости 

 .
.
Запишем разложение функции в ряд Лорана в каждом кольце. Для этого:
а) объединим первое и второе разложения. Тогда

 – ряд Тейлора, где
– ряд Тейлора, где 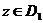 , так как для данных рядов области сходимости равны соответственно
, так как для данных рядов области сходимости равны соответственно  и
и  . Следовательно, в пересечении будет
. Следовательно, в пересечении будет  , а это и есть область D 1.
, а это и есть область D 1.
b) объединим второе и третье разложения. Тогда




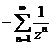 , где
, где  , так как для данных рядов области сходимости равны соответственно
, так как для данных рядов области сходимости равны соответственно  и
и 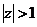 . Следовательно, в пересечении будет
. Следовательно, в пересечении будет  , а это и есть область D 2.
, а это и есть область D 2.
c) объединим третье и четвертое разложения. Тогда



 , где
, где 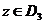 , так как для данных рядов области сходимости равны соответственно
, так как для данных рядов области сходимости равны соответственно 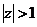 и
и  . Следовательно, в пересечении будет
. Следовательно, в пересечении будет  , а это и есть область D 3.
, а это и есть область D 3.
Пример 8. Разложить в ряд Лорана функцию  в точке
в точке 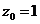 .
.
 Решение.
Решение.
Требуется найти разложение по степеням  . Найдем кольцевые области аналитичности функции f (z) с центром в точке
. Найдем кольцевые области аналитичности функции f (z) с центром в точке 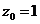 . Аналитичность функции нарушается в точках
. Аналитичность функции нарушается в точках 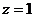 и
и  . Следовательно, кольцевыми областями будут: D 1:
. Следовательно, кольцевыми областями будут: D 1:  ; D 2:
; D 2:  ; D 3:
; D 3:  (рис. 45).
(рис. 45).
Разложим данную функцию на элементарные дроби:
 .
.
Рассмотрим отдельно каждое слагаемое и найдем их разложения в ряды в областях D 1, D 2, D 3.
1) Первое слагаемое в сумме 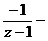 это уже разложение в ряд Лорана, область сходимости которого
это уже разложение в ряд Лорана, область сходимости которого  .
.
2) 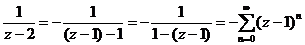 , область сходимости:
, область сходимости:  .
.
3) 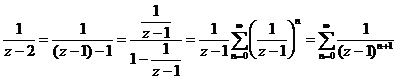 , область сходимости:
, область сходимости: 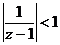

 .
.
Запишем разложение функции в ряд Лорана в каждом кольце.
а) 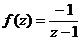 , где
, где 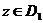 , т.е. область сходимости
, т.е. область сходимости  .
.
b) объединим первое и второе разложения. Тогда
 , где
, где  , так как для данных рядов области сходимости равны соответственно
, так как для данных рядов области сходимости равны соответственно  и
и  . Следовательно, в пересечении будет
. Следовательно, в пересечении будет  , а это и есть область D 2.
, а это и есть область D 2.
c) объединим первое и третье разложения. Тогда




 , где
, где 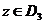 , так как для данных рядов области сходимости равны соответственно
, так как для данных рядов области сходимости равны соответственно  и
и  . Следовательно, в пересечении будет
. Следовательно, в пересечении будет  , а это и есть область D 3.
, а это и есть область D 3.
Пример 9. Разложить в ряд Лорана по степеням z функцию  в кольце
в кольце  (рис. 46).
(рис. 46).
 Решение.
Решение.
Разложим данную функцию на элементарные дроби:
 .
.
Учтем, что  и запишем функцию в виде:
и запишем функцию в виде:




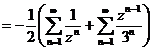 .
.
Пояснение: первое слагаемое разложили в окрестности бесконечно удаленной точки, так как область сходимости получившегося ряда  , т.е.
, т.е. 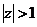 . Второе слагаемое разложили в окрестности нуля, так как область сходимости получившегося ряда
. Второе слагаемое разложили в окрестности нуля, так как область сходимости получившегося ряда  , т.е.
, т.е.  . Две области в пересечении дадут кольцо
. Две области в пересечении дадут кольцо  .
.
Пример 10. Разложить в ряд Лорана по степеням  функцию
функцию 
Решение.
Положим  , тогда
, тогда 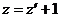 . При подстановке в функцию получим:
. При подстановке в функцию получим:
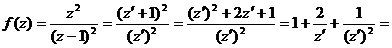 (перейдем к старому переменному)
(перейдем к старому переменному)  ,
,
где первое слагаемое 1 – правильная часть ряда Лорана, а  – главная часть ряда Лорана. Данное разложение справедливо для любой точки плоскости, кроме
– главная часть ряда Лорана. Данное разложение справедливо для любой точки плоскости, кроме 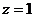 , так как содержит конечное число слагаемых.
, так как содержит конечное число слагаемых.
Пример 11. Разложить в ряд Лорана функцию  в окрестности точки
в окрестности точки 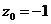 .
.
Решение.
Функция 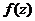 аналитична в области
аналитична в области  . Сделаем замену:
. Сделаем замену:  , тогда
, тогда  . Подставим в функцию:
. Подставим в функцию:

 , где
, где  или
или  . Тогда
. Тогда

 , где
, где  .
.
Пример 12. Найти область сходимости ряда Лорана  .
.
Решение.
Для решения задачи применим признак Коши:
 , отсюда
, отсюда 
 область сходимости
область сходимости  бесконечное кольцо.
бесконечное кольцо.