Ход урока.
Ι.Организационный момент.
ΙΙ. Повторение изученного материала.
Решетить задачу: (Громцева 1.4.5)

|
ΙΙI. Изучение новой темы.
Относительность движения.
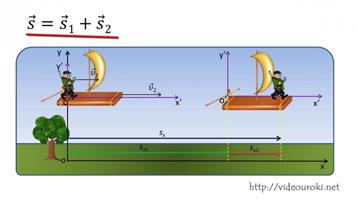
| Всякое движение относительно. Это означает, что одно и то же тело одновременно и движется, и покоится. Движется относительно одних тел и одновременно покоится относительно других. Мы все, земляне, можем покоиться относительно своего письменного стола и одновременно всегда движемся относительно Солнца. В задачах на относительность движения часто приходится пользоваться правилом сложения скоростей. Правило сложения скоростей: |
Классический закон сложения скоростей. Выясним, как связаны между собой скорости движения тела в различных системах отсчета. Рассмотрим такой пример. Вагон движется по прямолинейному участку железнодорожного пути равномерно со скоростью 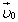 относительно Земли. Пассажир движется относительно вагона со скоростью
относительно Земли. Пассажир движется относительно вагона со скоростью 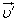 , векторы скоростей
, векторы скоростей 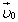 и
и 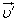 имеют одинаковое направление.
имеют одинаковое направление.
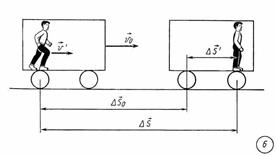
| Найдем скорость пассажира относительно Земли. Перемещение пассажира относительно Земли 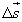 за малый промежуток времени Δt равно сумме перемещений за этот промежуток времени вагона относительно Земли за малый промежуток времени Δt равно сумме перемещений за этот промежуток времени вагона относительно Земли 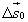 и пассажира относительно вагона и пассажира относительно вагона 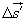 (рис. 6): (рис. 6):
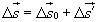 или
или
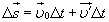 . .
|
Отсюда скорость пассажира относительно Земли 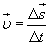 равна
равна 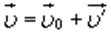 . (1.2)Мы получили, что скорость
. (1.2)Мы получили, что скорость  пассажира в системе отсчета, связанной с Землей, равна сумме скоростей
пассажира в системе отсчета, связанной с Землей, равна сумме скоростей  пассажира в системе отсчета, связанной с вагоном, и
пассажира в системе отсчета, связанной с вагоном, и  вагона относительно Земли.
вагона относительно Земли.
Этот вывод справедлив для любых направлений векторов скорости 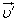 и скорости
и скорости 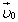 . Закон, выражаемый формулой (1.2), называется классическим законом сложения скоростей.
. Закон, выражаемый формулой (1.2), называется классическим законом сложения скоростей.
скорость тела относительно неподвижной системы отсчета 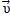 равна сумме скорости тела относительно подвижной системы отсчета
равна сумме скорости тела относительно подвижной системы отсчета 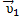 и скорости
и скорости 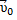 самой подвижной системы относительно неподвижной, где
самой подвижной системы относительно неподвижной, где
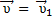 + + 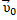
|
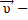 скорость тела относительно НСО
скорость тела относительно НСО
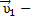 скорость тела относительно ПСО
скорость тела относительно ПСО
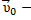 скорость ПСО относительно НСО
скорость ПСО относительно НСО
Это правило применимо только к классическим скоростям, т.е. скоростям, значительно меньшим скорости света в вакууме (т.е. к скоростям порядка 106 м/с и меньше).
1) Если система отсчета и тело в ней движутся в одном направлении, то 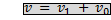
Например, если поезд движется со скоростью 16 м/с относительно вокзала, а пассажир по ходу поезда бежит со скоростью 2 м/с относительно полок вагона, то скорость пассажира относительно вокзала равна 18 м/с.
2) Если система отсчета и тело в ней движутся в противоположных направлениях, 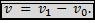
Например, если в предыдущем примере пассажир будет бежать навстречу ходу поезда, то скорость, с которой он будет удаляться от вокзала, будет равна 14 м/с
3) Если в подвижной системе отсчета, движущейся со скоростью относительно неподвижной системы, тело станет двигаться со скоростью относительно подвижной системы под углом к направлению ее движения, то для определения модуля скорости тела относительно неподвижной системы придется применить теорему Пифагора или теорему косинусов — в зависимости от величины угла 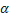 (рис. 10 а и б).
(рис. 10 а и б).
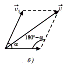
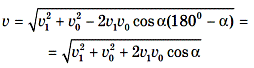
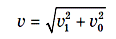

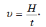
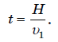 |
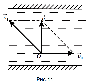
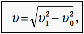
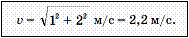 Например, если скорость течения v0 =1 м/с, а лодка переплывает реку со скоростью v1 = 2 м/с относительно воды перпендикулярно берегу (рис. 10), то скорость лодки относительно берега будет, согласно теореме Пифагора, равна
Например, если скорость течения v0 =1 м/с, а лодка переплывает реку со скоростью v1 = 2 м/с относительно воды перпендикулярно берегу (рис. 10), то скорость лодки относительно берега будет, согласно теореме Пифагора, равна

!!! Если в условии сказано, что лодка переплывает реку по кратчайшему пути, значит, ее скорость относительно берега  направлена перпендикулярно берегу, а скорость лодки относительно воды
направлена перпендикулярно берегу, а скорость лодки относительно воды  направлена под тупым углом к вектору скорости течения
направлена под тупым углом к вектору скорости течения 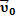 (рис. 11). В таком случае скорость лодки относительно берега можно определить по теореме Пифагора:
(рис. 11). В таком случае скорость лодки относительно берега можно определить по теореме Пифагора:
а время t, за которое лодка переплывет реку шириной Н, двигаясь с этой скоростью, можно найти как отношение этой ширины к скорости лодки относительно берега:
Если говорится о минимальном времени, за которое лодка переплывет реку, то теперь перпендикулярно берегу надо направить вектор скорости лодки относительно воды под прямым углом к течению, как на рис. 12. В этом случае минимальное время t будет равно отношению ширины реки к скорости лодки относительно течения:Таким образом, если вам нужно переплыть реку как можно быстрее, значит, надо грести перпендикулярно течению.
4) Если два тела сближаются или удаляются друг от друга, т.е. движутся в противоположных направлениях со скоростями v1 и v2 относительно неподвижных объектов, то их скорость v относительно друг друга будет по модулю равна сумме их скоростей относительно неподвижных объектов: 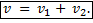
5) Если два тела обгоняют друг друга, т.е. движутся в одном направлении со скоростями v1 и v2 относительно неподвижных объектов, то их скорость v относительно друг друга по модулю будет равна разности их скоростей относительно неподвижных объектов: 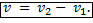
Например, если два поезда едут по параллельным рельсам навстречу друг другу со скоростями 36 км/ч и 74 км/ч относительно вокзала, то скорость их взаимного сближения, т.е. скорость первого поезда относительно второго по модулю равна скорости второго относительно первого и равна: 36 км/ч + 74 км/ч = 110 км/ч.
А если они движутся по параллельным рельсам в одном направлении, т.е., например, если второй поезд, скорость которого равна 72 км/ч, обгоняет первый, скорость которого 36 км/ч, то скорость первого поезда относительно второго равна скорости второго минус скорость первого:
72 км/ч – 36 км/ч = 36 км/ч,
а скорость второго поезда относительно первого равна скорости
первого поезда минус скорость второго: 36 км/ч – 72 км/ч = –36 км/ч.
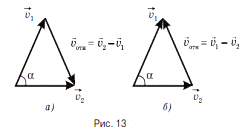
 6) Если два тела движутся со скоростями v1 и v2 относительно неподвижных объектов и векторы этих скоростей направлены под углом
6) Если два тела движутся со скоростями v1 и v2 относительно неподвижных объектов и векторы этих скоростей направлены под углом 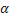 друг к другу, то, чтобы найти скорость второго тела относительно первого, надо найти векторную разность
друг к другу, то, чтобы найти скорость второго тела относительно первого, надо найти векторную разность 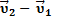 (рис. 13, а), а чтобы найти скорость первого тела относительно второго, надо найти векторную разность
(рис. 13, а), а чтобы найти скорость первого тела относительно второго, надо найти векторную разность 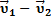 (рис. 13, б).
(рис. 13, б).
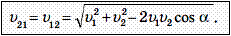 Для нахождения модуля относительной скорости можно применить теорему косинусов:
Для нахождения модуля относительной скорости можно применить теорему косинусов:
Если 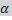 = 900, то удобно применить теорему Пифагора:
= 900, то удобно применить теорему Пифагора:
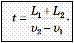
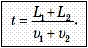
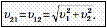 Если сказано, что два поезда длиной L 1 и L 2 каждый движутся навстречу друг другу со скоростями v 1 и v 2 относительно неподвижных объектов (деревьев, домов), то время t, в течение которого они будут проезжать мимо друг друга, можно найти, разделив сумму их длин на их скорость относительно друг друга, которая при встречном движении поездов равна сумме их скоростей:
Если сказано, что два поезда длиной L 1 и L 2 каждый движутся навстречу друг другу со скоростями v 1 и v 2 относительно неподвижных объектов (деревьев, домов), то время t, в течение которого они будут проезжать мимо друг друга, можно найти, разделив сумму их длин на их скорость относительно друг друга, которая при встречном движении поездов равна сумме их скоростей:
А если эти поезда обгоняют друг друга, двигаясь в одном направлении, то время обгона равно:
ΙV. Закрепление пройденного материала
Решение задач:

V. Домашнее задание. § 6