Пусть дано операторное уравнение: Az = u, где A - линейный оператор, действующий из нормированного пространства Z в нормированное пространство U. В 1963 г. А.Н.Тихонов дал знаменитое определение регуляризирующего алгоритма (РА), которое лежит в основе современной теории некорректно поставленных задач.
Определение. Регуляризирующим алгоритмом (регуляризирующим оператором) 
называется оператор, обладающий двумя следующими свойствами:
1) 
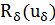определен для любых δ > 0, 
∈ U, и отображает (0,+ ∝) × U в Z;
2) для любого z ∈ Z и для любого ∈ U такого, что Az = u, 
.
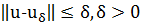
Задача решения уравнения первого рода называется регуляризируемой, если существует хотя бы один регуляризирующий алгоритм. Непосредственно из определения следует, что если существует хотя бы один РА, то их существует бесконечно много.
В настоящее время все математические задачи можно разделить на следующие классы:
1) корректно поставленные задачи;
2) некорректно поставленные регуляризируемые задачи;
3) некорректно поставленные нерегуляризируемые задачи.
Понятно, что корректно поставленные задачи являются регуляризируемыми, поскольку можноположить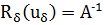 
. Отметим, что знание δ > 0 в этом случае необязательно.
Далеко не все некорректно поставленные задачи можно регуляризировать, причем это часто зависит от выбора пространств Z, U. Российский математик Л.Д.Менихес построил пример интегрального оператора с непрерывным замкнутым ядром, действующего из пространства C [0,1] в 
, обратная задача для которого (т.е. решение интегрального уравнения Фредгольма 1-го рода) является нерегуляризируемой. Это связано со свойствами пространства C [0,1]. Ниже будет показано, что если пространство Z гильбертово, а оператор A ограниченный и инъективный, то задача решения операторного уравнения первого рода является регуляризируемой. Этот результат справедлив и для некоторых банаховых пространств, но не для всех. В частности, пространство C [0,1] к таким банаховым пространствам не относится.
|
|
Можно дать эквивалентное определение регуляризирующего алгоритма и регуляризируемости операторного уравнения. Пусть задан оператор (отображение) 
, причем определен для любых δ > 0, ∈ U, и отображает (0,+ ∝) × U в Z. Погрешность решения операторного уравнения в точке z ∈ Z с помощью оператора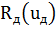 
при условии, что правая часть u задана с погрешностью δ >0, определяется как
Оператор 
называется регуляризирующим оператором, если для любого z ∈ Z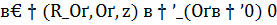 
. Легко видеть, что данное определение эквивалентно данному выше.
Аналогично можно дать определение регуляризирующего алгоритма для задачи вычисления значений оператора (см. конец предыдущего параграфа), т.е. для задачи вычисления значений отображения G: D (G) → Y, D (G) ⊆ X при условии, что аргумент задан с погрешностью (X, Y – метрические или нормированные пространства). Разумеется, задача решения операторного уравнения при условии, что A – инъективный оператор, может рассматриваться как задача вычисления значений оператора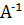 
.
Огромное значение имеет ответ на следующий очень важный вопрос, можно ли решить некорректную задачу, т.е. построить регуляризирующий алгоритм, не зная погрешность δ Если задача корректна, то устойчивый метод, очевидно, можно построить и без знания δ.
|
|
Так, в случае решения операторного уравнения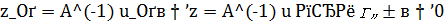 
. В случае некорректных задач это невозможно. Приведенная ниже теорема принадлежит А.Б.Бакушинскому и была им доказана для задачи вычисления значений оператора. Аналогичная теорема имеет место и для решения операторного уравнения.
Теорема. Если для вычислений значений оператора G на множестве D (G) ⊆ X существует регуляризирующий оператор, не зависящий от δ (явно), то существует продолжение G на X, которое непрерывно на D (G) ⊆ X.
Итак, построение регуляризирующих алгоритмов, не зависящих явно от погрешности,
возможно только для задач, корректных на своей области определения.
Следующим свойством некорректно поставленных задач является невозможность оценить погрешность решения, даже если известна погрешность задания правой части операторного уравнения или погрешность задания аргумента в задаче вычисления значений оператора. Этот принципиально важный результат был также впервые доказан А.Б.Бакушинским для решения операторного уравнения.
Теорема. Пусть 
для любого z ∈ D ⊆ Z. Тогда сужение обратного оператора на множество AD: 
непрерывно на AD. Таким образом, равномерная по z оценка погрешности решения операторного уравнения на множестве D ⊆ Z возможна только в том случае, когда обратный оператор непрерывен на AD. Таким образом, равномерная по z оценка погрешности решения операторного уравнения на множестве D ⊆ Z возможна только в том случае, когда обратный оператор непрерывен на AD. Данная теорема справедлива и для нелинейных операторных уравнений, причем в метрических пространствах.
|
|
Из определения регуляризирующего алгоритма легко следует, что, если есть хотя бы один регуляризирующий алгоритм, то их может быть сколько угодно. Выбрать же тот, который дает наименьшую ошибку, или сравнивать алгоритмы, сравнивая ошибки полученных приближенных решений, при решении некорректных задач, невозможно при отсутствии априорной информации, которая фактически преобразует такие задачи в корректные.
Регуляризирующие алгоритмы для операторных уравнений в бесконечномерных банаховых пространствах нельзя сравнивать и по скорости сходимости приближенного решения к точному при стремлении погрешности входных данных к нулю. Этот важный результат принадлежит В.А.Винокурову. (Ист. №1)