Степенные ряды и их свойства.

Ряды.

Основные положения.

a1, a2, a3, …, an – числовой ряд.

- сумма ряда. Сумма n первых членов ряда называется частичной суммой ряда.

Ряд называется сходящимся, если существует конечный предел последовательности частичных сумм, иначе – расходящийся.

Свойства сходящихся рядов:

1. Если ряд сходится, то любое отбрасывание конечного числа членов не влияет на сходимость;
2. Если ряд сходится, то умножение на const не влияет на сходимость;
3. Пусть есть 2 сходящихся ряда, тогда .

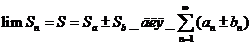Необходимый признак сходимости ряда:

Если - сходящийся ряд, то .

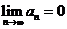Доказательство:

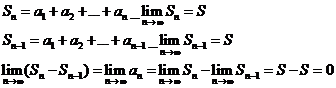
Практически удобно использовать обратное утверждение – если предел не равен нулю, то ряд расходится.

Достаточные признаки сходимости:

1. Признак Даламбера – удобно применять для рядов, где в формуле есть показательная функция и факториал -
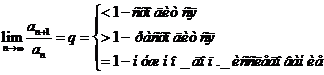
2. Радикальный признак Коши -
3. Интегральный признак Коши -

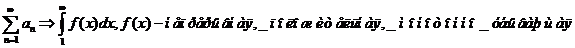
Ряд ведет себя так же, как и интеграл;

1. Теоремы сравнения:

а)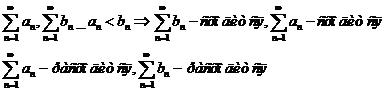

б) 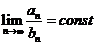- ряды ведут себя одинаково.

Понятие абсолютной и условной сходимости используется для знакопеременных (частный случай – знакочередующихся) рядов.

Теорема: пусть дан знакопеременный ряд, для которого составлен ряд из модулей. Если ряд из модулей сходится, то сходится и исходный ряд (в этом случае говорят об абсолютной сходимости).

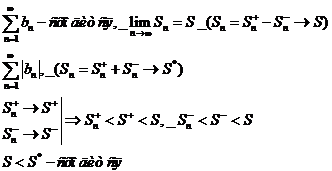
Данное условие является достаточным условием. В случае, когда ряд из модулей расходится, а исследуемый исходный ряд сходится, говорят об условной сходимости.

Признак Лейбница: пусть дан знакочередующийся ряд и выполняются условия 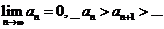- тогда говорят, что исходный ряд сходится условно.

Функциональные ряды.

- функциональный ряд. Если рассмотреть все x, при которых ряд сходится, то область D – область сходимости функционального ряда. Для исследования сходимости в общем виде функционального ряда составляется ряд из модулей и получается знакоположительный ряд. Для дальнейших исследований данного знакоположительного ряда можно использовать все известные признаки для знакоположительных рядов.

Для конечных сумм известно:

1. Суперпозиция конечного числа непрерывных функций есть непрерывная сумма;
2. Производная суммы конечного числа функций есть сумма производных;
3. Интеграл от суммы конечного числа функций есть сумма интегралов.

А для бесконечной суммы?

С бесконечными суммами надо обращаться аккуратно.

Равномерная сходимость.

- сходится. Тогда по определению 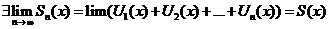, . По определению предела 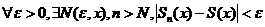- определение простой сходимости. Для равномерной сходимости . Для равномерной сходимости рядов справедливы следующие свойства:

1. Если члены равномерно сходящегося ряда непрерывны, то и сумма ряда S(x) – непрерывная функция;
2. Равномерно сходящийся ряд можно почленно дифференцировать и интегрировать.

Степенные ряды и их свойства.

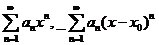- степенные ряды.

. Через радиус сходимости находим области сходимости и расходимости. Граничные точки нужно исследовать дополнительно. Аналогично формулу радиуса можно получить, используя признак Коши , , . Степенные ряды на области сходимости можно почленно дифференцировать и интегрировать, причем любое число раз.

Функцию, которая в окрестности точки x определена и дифференцируема сколько угодно раз, в окрестности данной точки можно приближенно представить (аппроксимировать) степенным рядом.

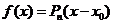
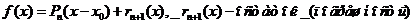
Ряд Маклорена – частный случай ряда Тейлора - .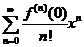

С помощью данных рядов можно приближенно находить значения функций и приближенно считать неберущиеся интегралы.