Интегралы
Методические указания
и индивидуальные задания
для выполнения типового расчета
Хабаровск
Издательство ДВГУПС
УДК 517.3 (075.8)
ББК В 161.12 я73
Ш 284
Рецензент:
Кандидат физико-математических наук,
доцент кафедры «Высшая математика» Дальневосточного
государственного университета путей сообщения
Г.П. Кузнецова
| Ш 284 | Шатилова, Л.Н. Интегралы: методические указания /Л.Н. Шатилова, М.А. Городилова, Т.Г. Плотникова. – Хабаровск: Изд-во ДВГУПС, 2005. – 68 с.: ил. |
В методических указаниях даны рекомендации по выполнению типового расчета по теме «Интегралы, приложения определенного интеграла».
Даны варианты индивидуальных заданий.
Указания предназначены для студентов всех специальностей железнодорожного вуза.
УДК 517.3 (075.8)
ББК В 161.12 я73
ã ГОУ ВПО «Дальневосточный государственный
университет путей сообщения» (ДВГУПС), 2005
ВВЕДЕНИЕ
Настоящее издание написано в соответствие с программой по курсу высшей математики для втузов и ставит своей целью помочь студенту овладеть методами интегрирования. Это определило структуру пособия. В начале приведены теоретические вопросы, затем предлагаются теоретические упражнения. Для каждого метода интегрирования даны ссылки на методическое пособие«Интегральное исчисление функции одной переменной» (Л.Н. Гамоля, Г.П. Кузнецова, Л.В. Марченко Издательство ДВГЦУПС 2004г.).
Указания содержат варианты индивидуальных заданий для студентов ДВГУПС дневной формы обучения.
ПРЕДИСЛОВИЕ
Интегральное исчисление – это раздел математического анализа, в котором изучаются интегралы, их свойства, способы вычисления и приложения. Вместе с дифференциальным исчислением оно составляет основу аппарата математического анализа.
Интегральное исчисление возникло из рассмотрения большого числа задач естествознания и математики. Важнейшие из них – физическая задача определения пройденного за данное время пути по известной, но переменной скорости движения и значительно более древняя задача вычисления площадей и объемов геометрических фигур.
Центральным в интегральном исчислении является понятие интеграла, которое имеет две различные трактовки, приводящие к понятиям неопределенного и определенного интегралов.
Рассматриваемая в интегральном исчислении обратная к дифференцированию математическая операция, называется интегрированием, которая состоит в отыскании первообразной данной функции. Заметим, что, наряду с функцией F(x), первообразной для функции f(x), будет также любая функция F(x) + С, отличающаяся от F(x) постоянным слагаемым С, ведь (F(x) + С)1 = F(x)1 = f(x). Таким образом, в отличие от дифференцирования, сопоставляющего функции единственную другую функцию – производную первой, неопределенное интегрирование приводит не к одной конкретной функции, а к целому набору функций, и в этом его неопределенность.
Укажем более древний подход к интегралу, который послужил основным первоначальным источником интегрального исчисления, привел к понятию определенного интеграла или интеграла в собственном смысле этого слова. Этот подход четко прослеживается уже у древнегреческого математика и астронома Евдокса Книдского (примерно 408-355 до н.э.) и Архимеда, т. е. он возник задолго до появления дифференциального исчисления и операции дифференцирования.
Вопрос, который рассматривали Евдокс и Архимед, создав при его решении «метод исчерпывания», предвосхитивший понятие интеграла, – это вопрос о вычислении площади криволинейной фигуры.
Позднее эта задача была разрешена и представлена знаменитым соотношением: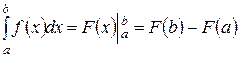 
, которое носит название «формула Ньютона-Лейбница». Полученная 
формула связывает интегрирование и дифференцирование.
МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ
Перед выполнением типового расчета необходимо изучить теоретический материал каждого раздела методического пособия «Интегральное исчисление функции одной переменной» (Л.Н. Гамоля, Г.П. Кузнецова, Л.В. Марченко. Издательство ДВГУПС 2004 г.).
Для успешного решения примеров первой части типового расчета надо выучить следующие параграфы 
выше указанного пособия:
– с 1 по 14 пример – параграфы 1 и 2 «Понятие первообразной функции и неопределенного интеграла» (стр. 4–11).
– с 15 по 17 примеры – параграф 3.2 «Интегрирование выражений, содержащих квадратный трехчлен в знаменателе» (стр. 14–15).
– с 18 по 21 пример – параграф 3.3 «Интегрирование рациональных дробей» (стр. 15–20).
– с 22 по 27 пример – параграф 3.1 «Метод интегрирования по частям» (стр. 11–13).
– с 28 по 31 (или 32, в зависимости от варианта) – параграф 3.4 «Интегрирование некоторых классов тригонометрических функций» (стр. 21–25).
– с 32(или 33) по 36 примеры – параграфы 3.5, 3.6 и 3.7 «Интегрирование некоторых иррациональных функций», «Интегрирование дифференциального бинома», «Подстановки Эйлера» (стр. 25–32).
– 37 и 38 примеры – параграфы 4, 5, 6, 8 «Задачи, приводящие к понятию определенного интеграла», «Определенный интеграл его свойства и вычисление» (стр. 36–54).
– 39 и 40 примеры – параграф 9 «Несобственные интегралы» (стр. 55– 63).
Для решения примеров второй части типового расчета надо изучить параграф 10 «Приложения определенного интеграла».
II. 1. – пункт 10.3 «Вычисление площади в декартовых координатах» (стр.66-68).
2. – пункт 10.4 «Вычисление площади в полярных координатах». (стр.69 – 71)
3. – пункт 10.5 «Вычисление площади фигуры, кривой, заданной в параметрическом виде» (стр. 72–73).
III. Пункт 10.6 «Вычисление длины дуги кривой» (стр. 74–78).
IV. Пункт 10.7, 10.8 «Вычисление объемов тел» (стр. 78–82).
V. Пункт 10.9 «Вычисление площади поверхности вращения» (стр.83–86).
Авторы желают уважаемым читателям успехов в изучении интегрального исчисления и рекомендуют не ограничиваться только одним пособием, но и использовать другую литературу по данной теме.
Теоретические вопросы
1. Понятие определённого интеграла, его геометрический смысл.
2. Основные свойства определённого интеграла.
3. Теорема о среднем.
4. Производная определённого интеграла по верхнему пределу.
5. Понятие первообразной функции. Теоремы о первообразных. Формула Ньютоны-Лейбница.
6. Неопределённый интеграл, его свойства.
7. Таблица неопределённых интегралов.
8. Замена переменной в неопределённом и определенном интегралах.
9. Интегрирование по частям в неопределённом и определенном интегралах.
10. Разложение дробно-рациональной функции на простейшие дроби.
11. Интегрирование простейших дробей.
12. Интегрирование рациональных функций.
13. Интегрирование выражений, содержащих тригонометрические функции.
14. Интегрирование иррациональных выражений.
15. Интегрирование биномиальных дифференциалов.
16. Вычисление площадей плоских фигур.
17. Определение и вычисление длины дуги кривой.
17. Вычисление объёмов тел вращения.
18. Вычисление площади поверхности тел вращения.