Определение наличия циклических колебаний.

ПАРНАЯ РЕГРЕССИЯ

Если результат зависит от одного фактора, то уравнение, описывающее заданную зависимость, является уравнением парной регрессии.

Пример 1. Заданы статистические данные о влиянии стажа работы на среднюю выработку рабочих:

Стаж работы (лет) Х

Средняя выработка (шт.) У

Необходимо: найти несколько видов уравнения регрессии (линейное, степенное и т.д.), выбрать «лучшее» (по R²), сделать прогноз для Х = 35.

Решение будем производить в EXCEL. Сначала найдем линейное уравнение

Вводим исходные данные. (Рисунок 1)

Рисунок 1

Выделяем введенные данные, далее нажимаем Вставка, Диаграммы, Точечная. (Рисунок 2)

Рисунок 2

После выбора типа точечной диаграммы (например, 1-ый) появляются точки (X, Y) - геометрическое изображение заданной зависимости. (Рисунок 3)

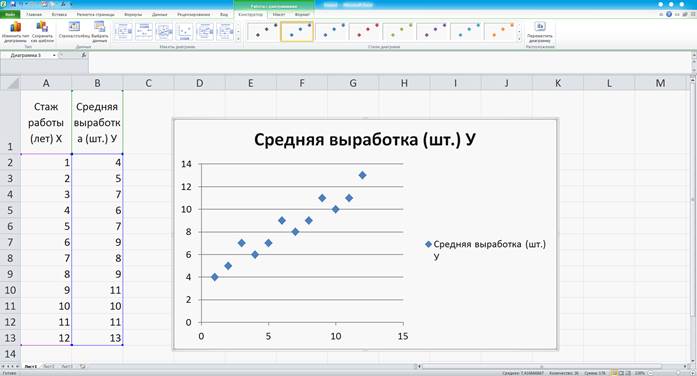
Рисунок 3

Правой клавишей мышки нажимаем на любую точку. (Рисунок 4)

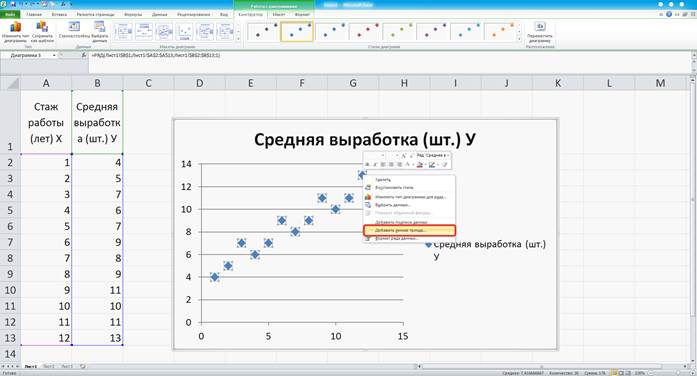
Рисунок 4

В появившемся окне выбираем Добавить линию тренда. В новом окне отмечаем параметры линии тренда: Линейная, показать уравнение на диаграмме, поместить на диаграмму величину достоверности аппроксимации R². (Рисунок 5)

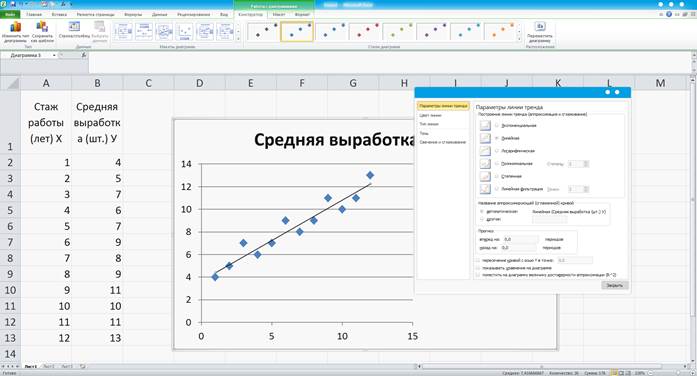
Рисунок 5

После закрытия окна получим (Рисунок 6).

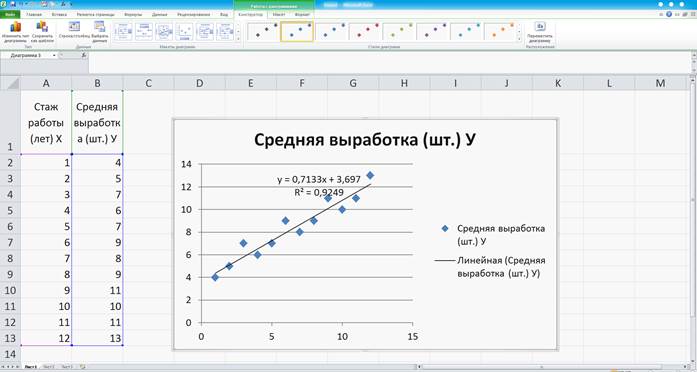
Рисунок 6

Таким образом, линейное уравнение парной регрессии будет: Y= 0,7133х+3,697

Величина R² говорит о том, что качество связи не достаточно высокое.

Так как R² =0,9249, то только 92,49% величины изменения У вызвано изменением Х.

Для линейной зависимости еще определяют тесноту связи коэффициентом корреляции r_xy. Известно, что -1 ≤ r_xy ≤ 1. Чем ближе абсолютная величина r_xy к 1, тем теснее связь.

Для нахождения r_xy нужно выделить ячейку, куда он будет помещен, ввести в нее «= », далее ФОРМУЛЫ, ДРУГИЕ ФУНКЦИИ, СТАТИСТИЧЕСКИЕ, КОРРЕЛ. (Рисунок 7)

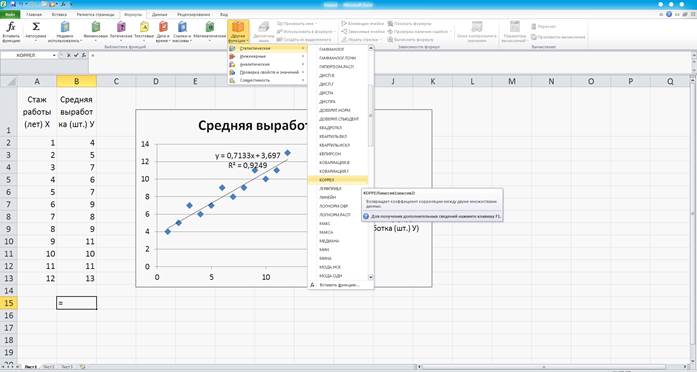
Рисунок 7

В появившемся окне заполняем МАССИВ 1 – ячейки, в которых находятся значения Х, МАССИВ 2 - ячейки, в которых находятся значения У. (Рисунок 8)

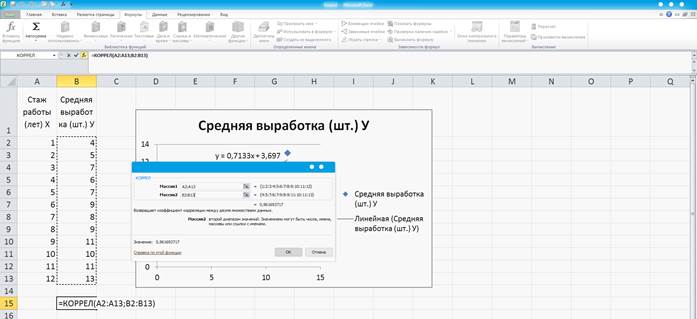
Рисунок 8

После нажатия ОК в выделенной ячейке появится значение 0,961693717.

Определим другие виды уравнения регрессии. Последовательность действий:

1) выделяем исходные данные;

2) далее Вставка, Диаграммы, Точечная;

3) выбор вида точечной диаграммы, правой клавишей мышки обозначаем любую точку;

4) далее выбираем Добавить линию тренда;

5) отмечаем параметры линии тренда: Вид линии, показать уравнение на диаграмме, поместить на диаграмму величину достоверности аппроксимации R².

Получим следующие уравнения, их геометрические изображения и оценки качества. (Рисунок 9);(Рисунок 10);(Рисунок 11) (2-я степень);(Рисунок 12) (3-я степень);(Рисунок 13)

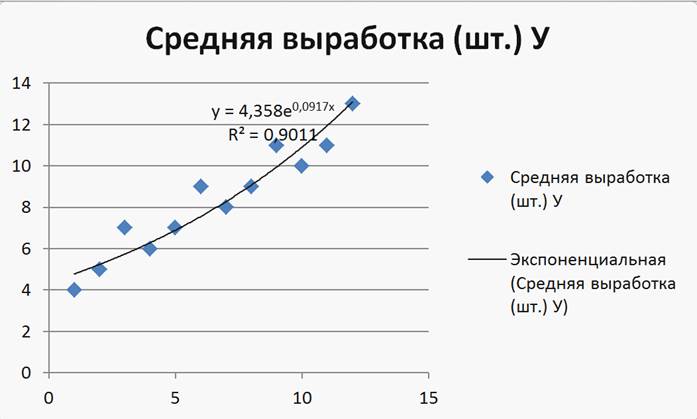
Рисунок 9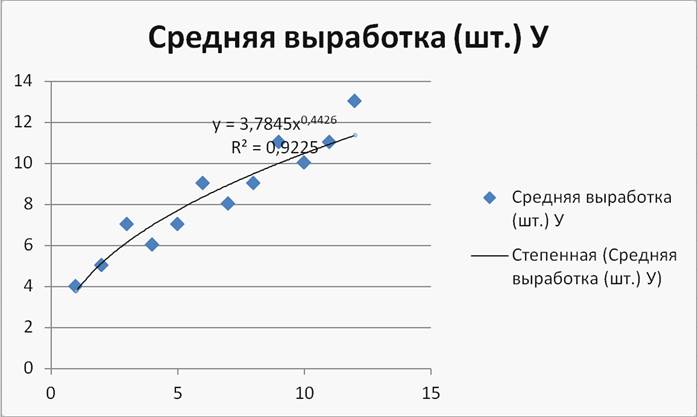

Рисунок 10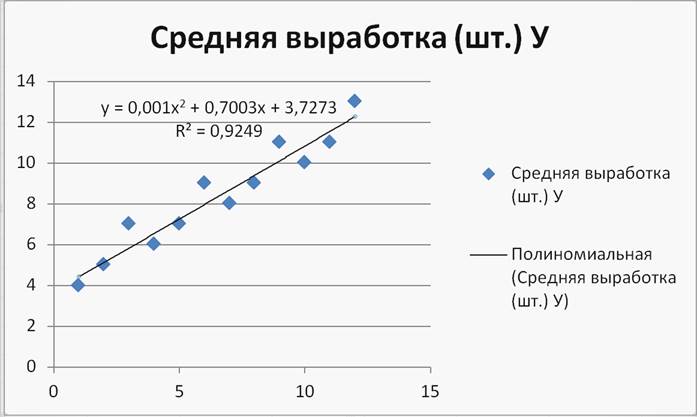

Рисунок 11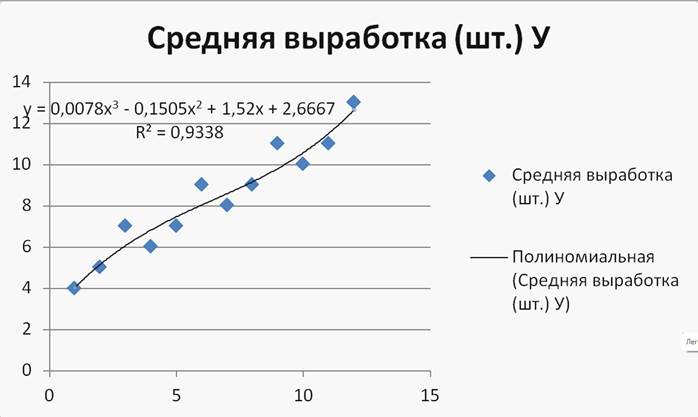

Рисунок 12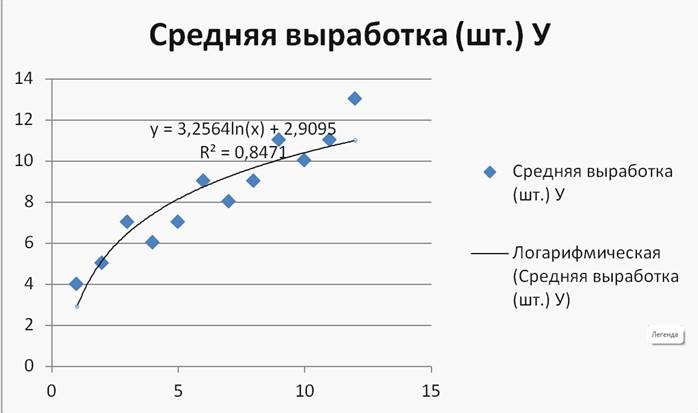

Рисунок 13

Видим, что самое высокое качество имеет полиномиальная связь 3-ей степени(R2 = 0,9338). Сделаем прогноз по данному уравнению:

Y (35) = 0,0078х³-0,1505х²+1,52х+2,6667 = 0,0078*35³-0,1505*35²+1,52*35+2,6667 = 205,9295

Можно при указании параметров линии тренда указать еще прогноз. (Рисунок 14)

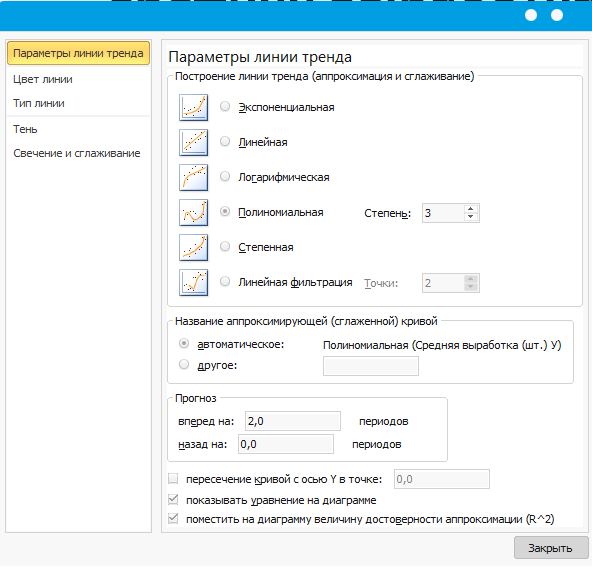
Рисунок 14

Получим прогнозную кривую. (Рисунок 15)

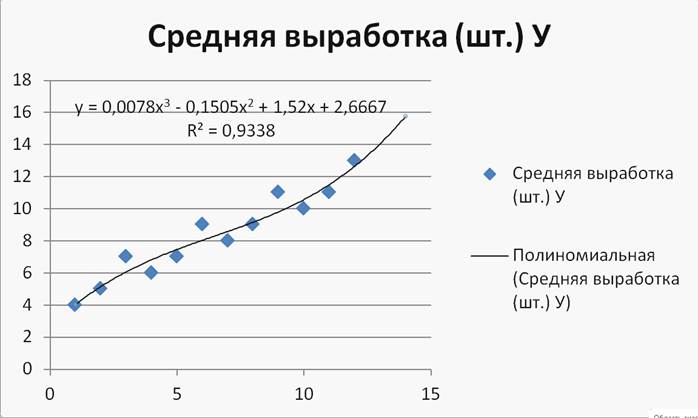
Рисунок 15

Пример 2. По 17 регионам изучается зависимость среднемесячной заработной платы (У) от инвестиций в основной капитал на душу населения (Х).

После введения данных отсортируем их по Х: Данные, Сортировка, по Х. (Рисунок 16)

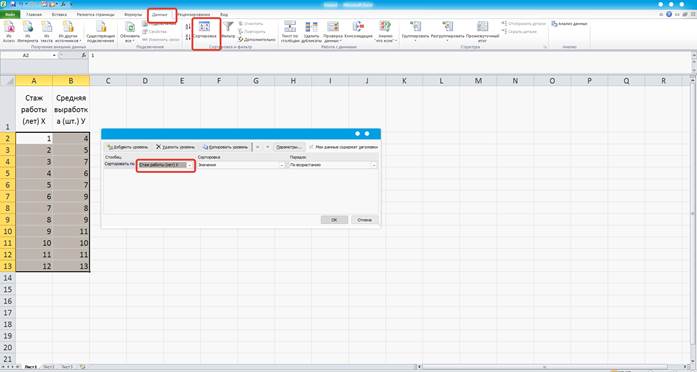
Рисунок 16

После ОК получим. (Рисунок 17)

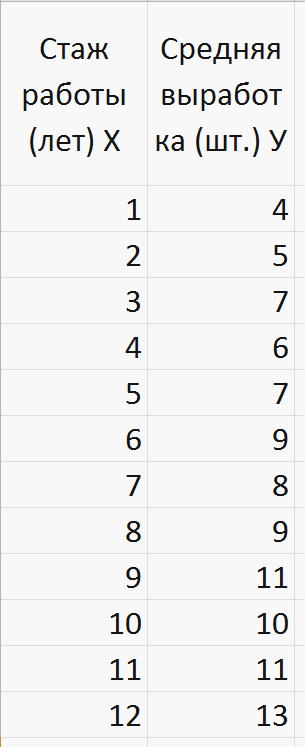
Рисунок 17

Аналогично предыдущему примеру получим ряд уравнений регрессии. (Рисунок 18);(Рисунок 19) (2-я степень);(Рисунок 20);(Рисунок 21);(Рисунок 22) (3-я степень)

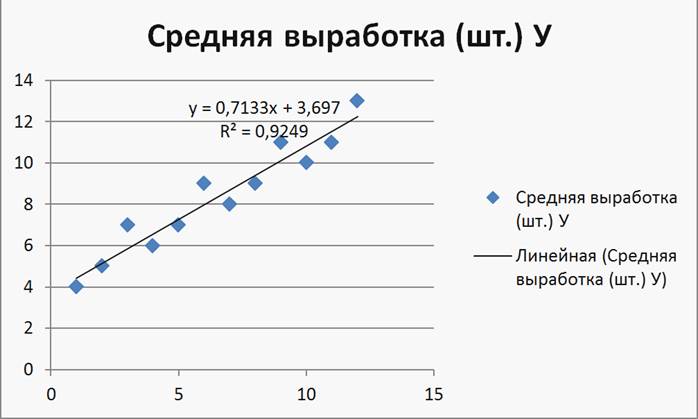
Рисунок 18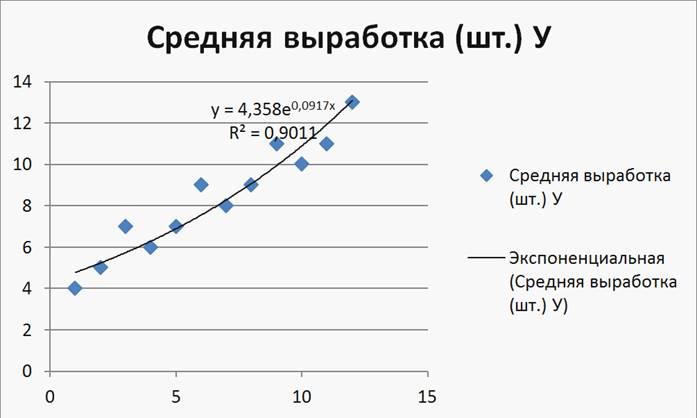

Рисунок 19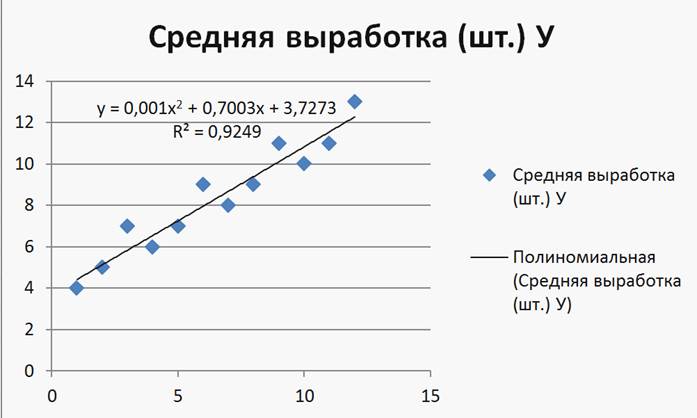

Рисунок 20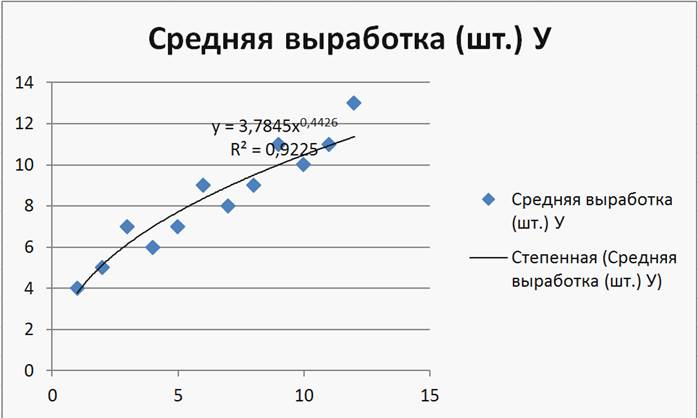

Рисунок 21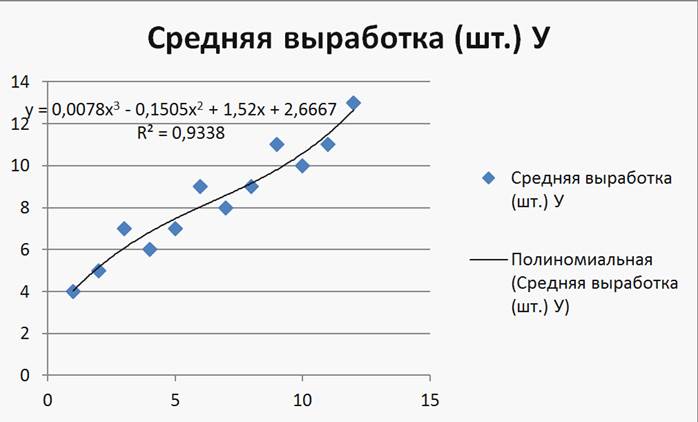

Рисунок 22

Наибольшее значение R² имеет для уравнения 3-ей степени(R2 = 0,9338). Сделав прогноз по данной зависимости (при определении параметров линии тренда), видим, что в прогнозируемом периоде результат уменьшается. Это связано с тем, что выбранная линия на интервале прогноза имеет максимум. (Рисунок 23)

Рисунок 23

Поэтому для прогноза выберем линейную зависимость (наибольший R² среди остальных зависимостей)

Y(13) = 0,7133*13+3,697 = 12,9699

Используя Параметры линии тренда, получим (Рисунок 24)

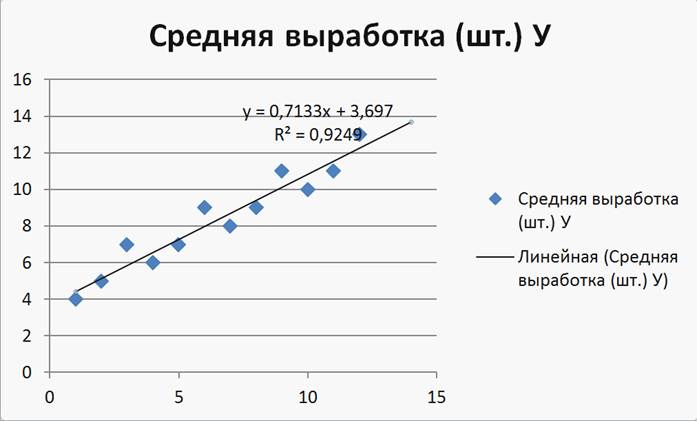
Рисунок 24

МНОЖЕСТВЕННАЯ РЕГРЕССИЯ (результат зависит от нескольких факторов)

Если результат У зависит от факторов Х₁, Х₂, ………, Х_n, то чаще всего используется два вида уравнения регрессии:

1) Yt = a + b1*X₁ + b2*X₂+…….+ bn*X_n - линейное уравнение

2) Yt = a*X1^b1*Х2^b2*…………*X_n^bn - степенное уравнение.

При этом предполагается, что факторы независимы между собой. Качество связи результата У с факторами определяется с помощью индекса детерминации R², который определяется с помощью встроенных программ или вычисляется по формуле

R² = 1 - 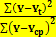, где

У - заданные значения результата;

Y_t - значения результата, полученные по уравнению регрессии;

У_ср - среднее значение У (У_ср = ), k- число наблюдений.

Для определения линейного уравнения регрессии будем пользоваться процедурой Анализ данных, для нелинейного – процедурой Поиск решения. Обе процедуры находятся во вкладке Данные. Если этих процедуры отсутствуют, то их необходимо активизировать следующим образом: Файл, Параметры, Надстройки, Надстройки Excel, Перейти, выбрать Пакет анализа и Поиск решения, ОК.

Пример 3. Имеются данные по 15 экономическим регионам (Рисунок 25). Обозначим

У - стоимость валового регионального продукта в этом году (млн. грн.).

Х₁ - инвестиции в экономику региона в этом году (млн. грн.).

Х₂ - инвестиции в экономику региона в прошедшем году (млн. грн.).

Х₃ - среднегодовая стоимость основных фондов в экономике региона (млн. грн.).

Х₄ - среднегодовая численность занятых в экономике региона (млн. чел.).

Рисунок 25

Для проверки линейной независимости факторов определим парные коэффициенты корреляции. Введем соответствующие обозначения. (Рисунок 26)

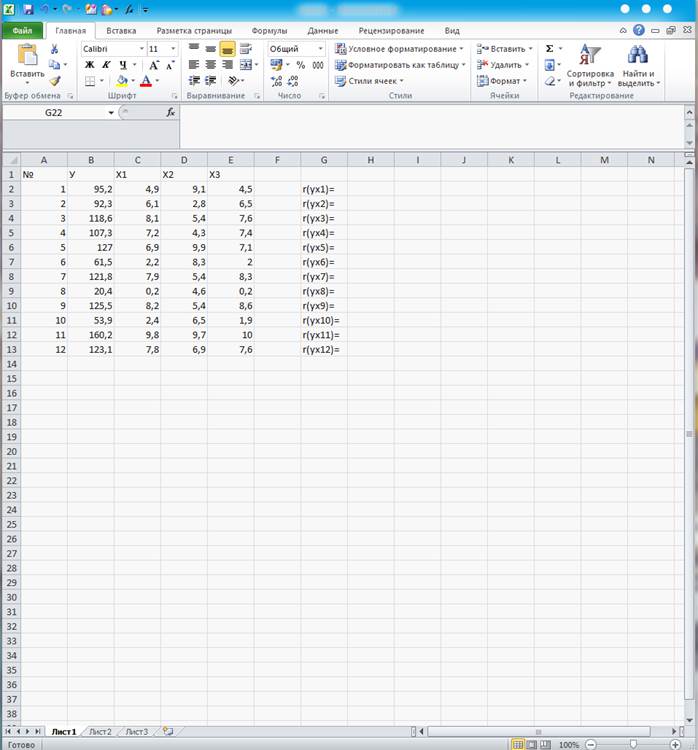
Рисунок 26

Выделим ячейку (Н2) для записи значения коэффициента корреляции между результатом У и фактором Х₁ r(yx1). В ячейку запишем знак «= », далее ФОРМУЛЫ, ДРУГИЕ ФУНКЦИИ, СТАТИСТИЧЕСКИЕ, КОРРЕЛ. В появившемся окне укажем ячейки, в которых находятся значения У и Х₁. (Рисунок 27)

Рисунок 27

После «ОК » получим (Рисунок 28):

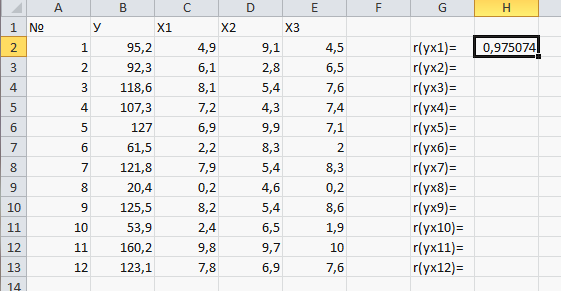
Рисунок 28

Протянув полученное значение по остальным ячейкам, получим (Рисунок 29)

Рисунок 29

Видим, что между факторами Х₁ и Х₃ тесная линейная связь (r = 0,994611). Поэтому один из факторов исключим. Исключим фактор, связь которого с результатом У слабее, т.е. Х₂, так как r(ух3) < r(yx1). (Рисунок 30)

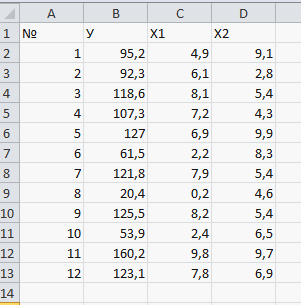
Рисунок 30

Для нахождения и анализа линейной регрессии необходимо: Данные, Анализ данных. В появившемся окне выбираем Регрессия. (Рисунок 31)

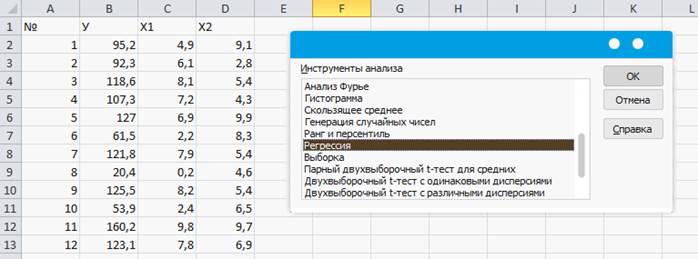
Рисунок 31

После ОК получим (Рисунок 32):

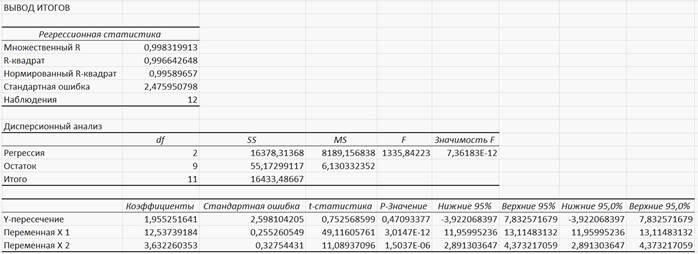
Рисунок 32

Чтобы увидеть интересующие нас данные, расширим столбцы В и С. Желтым цветом выделим интересующие нас величины. (Рисунок 33)

Рисунок 33

Видим, что R² ≈ 0,996643, a≈1,955252, b1≈12,53792, b2 ≈3,63226. Таким образом, искомое уравнение будет:

Yt = 1,955252+1,12,53792*X1+3,63226*X2.

Так как качество связи достаточно хорошее (R² > 0,7), то полученное уравнение можно использовать для прогноза. Для этого достаточно подставить в данное уравнение соответствующие значения Х1, Х2. Например, для Х1=10, Х2=10 получим:

Yt= 1,955252+12,53792*10+3,63226*10=163,657052

Если качество линейной связи недостаточно хорошее (R² < 0,7), то нужно искать нелинейное уравнение (степенное).

 

ФУНКЦИЯ КОББА-ДЕГЛАСА

Если изучается зависимость выпуска продукции от затрат труда и затрат фондов с помощью степенной функции, то такая функция называется функцией Кобба- Дугласа и имеет вид

Y = a₀*L^а1*K^a2

Пример 4.

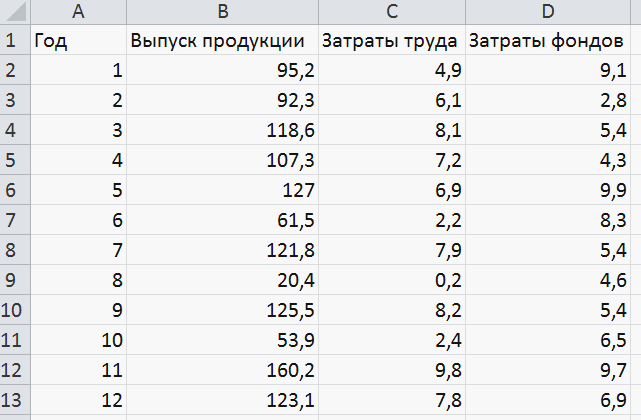
Рисунок 34

Найти функцию Кобба – Дугласа, определить качество полученной связи и сделать прогноз выпуска продукции при L = 8, K = 7.

Решаем в EXCEL. Искомое уравнение (как и любое нелинейное) найдем из условия:

∑ (Y-Yt)² → max

Вводим исходные данные, даем начальные значения искомым константам (например 1), записываем формулу для нахождения искомой функции при L = 4,9; К = 9,1 (ПЕРВЫЙ ГОД).

После ОК, протягивания по остальным ячейкам, в (F 2) запишем формулу для вычисления (Y – Yt)²: (Рисунок 35)

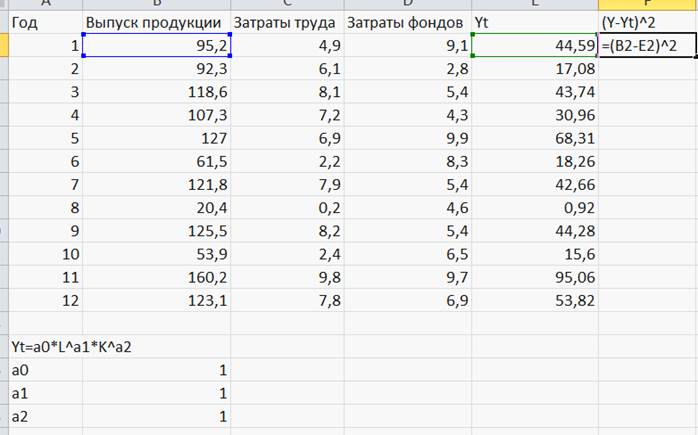
Рисунок 35

После ОК и протягивания (Рисунок 36):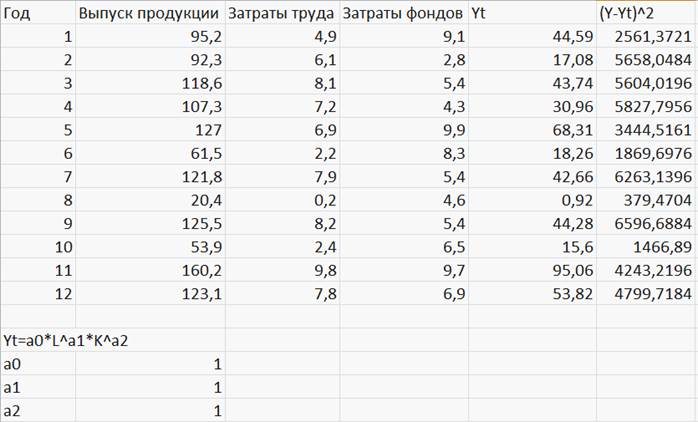

Рисунок 36

Суммируем найденные значения: «=», ФОРМУЛЫ, МАТЕМАТИЧЕСКИЕ, СУММ. (Рисунок 37)

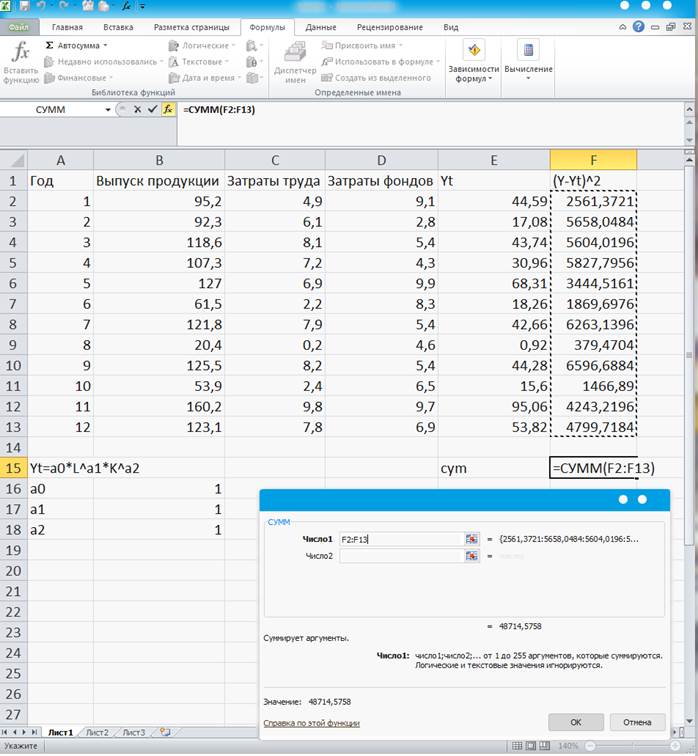
Рисунок 37

После ОК найдем среднее значение У: «=», ФОРМУЛЫ, ДРУГИЕ ФУНКЦИИ, СТАТИСТИЧЕСКИЕ, СРЗНАЧ. (Рисунок 38)

Рисунок 38

Вычисляем (У - Уср)² и находим сумму: (Рисунок 39)

Рисунок 39

Можно также в исходные данные ввести и прогнозные значения для L и K. (Рисунок 40)

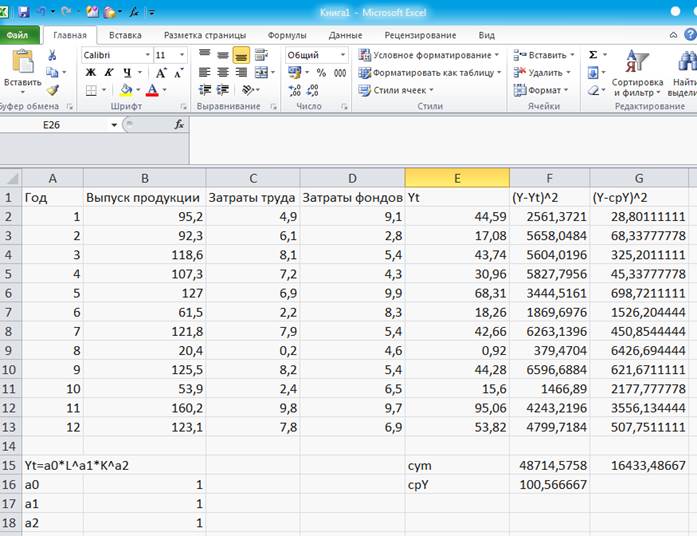
Рисунок 40

Нужно определить значения констант при которых сумма в F15 будет минимальной. Для этого → Данные, Поиск решения.

В появившемся окне указать номер ячейки, где находится минимизируемая сумма (целевая функция), что ищем минимальное значение, и какие ячейки нужно изменять (где находятся значения искомых констант). (Рисунок 41)

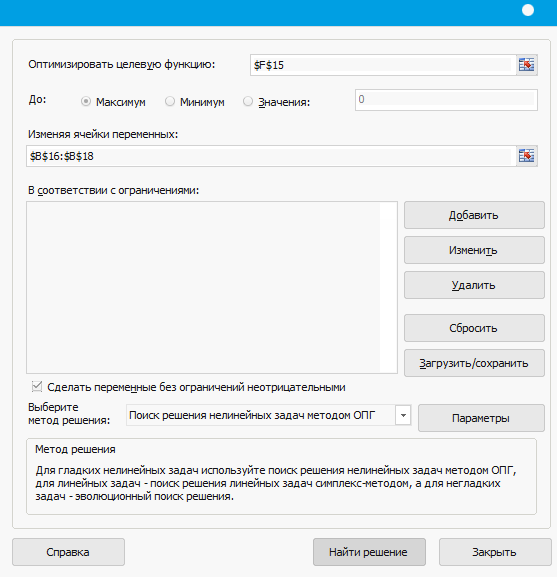
Рисунок 41

После Выполнить получим (Рисунок 42):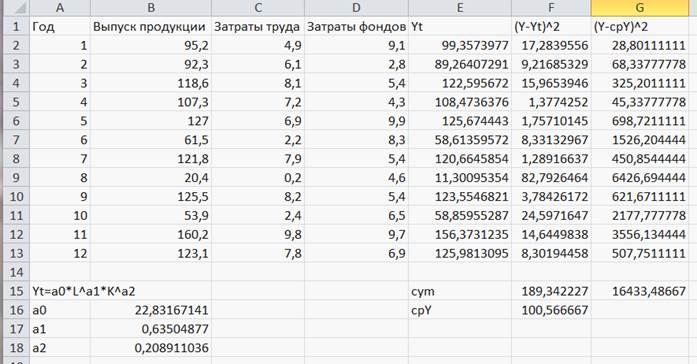

Рисунок 42

В ячейку F18 запишем формулу для вычисления R². (Рисунок 43)

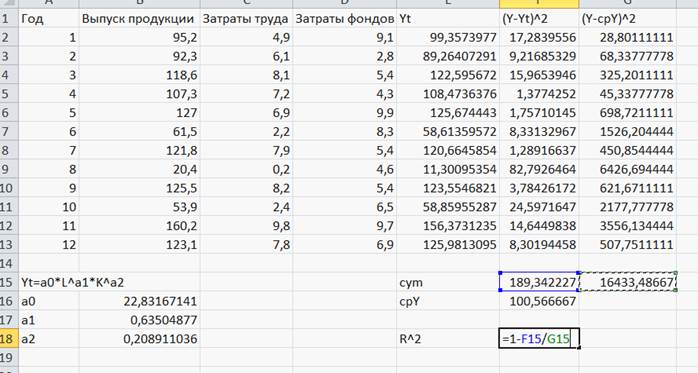
Рисунок 43

После Enter получим (Рисунок 44):

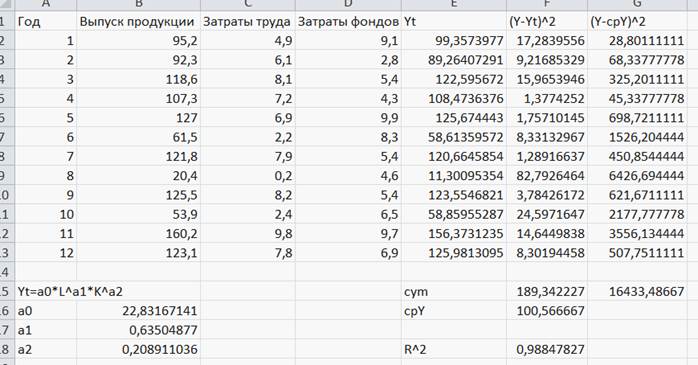
Рисунок 44

Таким образом, искомое уравнение будет

Y = 22,8317₀*L^0,6351*K^0,2089

Величина R² говорит о высоком качестве полученной связи (95,9 % величины изменения выпуска продукции У вызвано изменением затрат труда L и затрат фондов К).

Сделаем прогноз:

Yt (8,7) = 22,8317*8^0,6351*7^0,2089=128.419709

Или подставим значения L и K в таблицу (Рисунок 45):

P.S. Выбор начальных значений искомых констант может влиять на окончательное решение. Целесообразно произвести расчеты для нескольких наборов начальных значений констант (от 0 до 1) и выбрать тот, для которого R² больше.

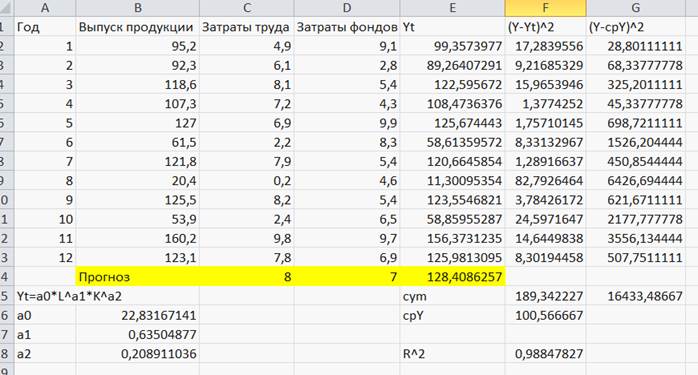
Рисунок 45

 

 

ВРЕМЕНЫЕ РЯДЫ

Временным рядом называется совокупность значений какого-либо показателя за несколько последовательных моментов (периодов) времени.

Простейший анализ временного ряда предполагает:

1) Определение наличия циклических колебаний ряда;

2) Построение аналитической функции, характеризующей зависимость уровней ряда от времени (определение тренда) и оценка качества полученной зависимости;

3) В случае зависимости членов ряда от предыдущих (автокорреляция) найти эту зависимость и оценить ее качество.

Определение наличия циклических колебаний.

Пример 5. Имеются данные об объемах потребления электроэнергии за 16 кварталов (млн кВт.ч).

t

Yt

Для определения наличия циклической составляющей временного ряда необходимо определить линейные коэффициенты корреляции между уровнями исходного ряда и уровнями этого ряда, сдвинутыми на несколько шагов во времени. Если наибольшее значение имеет коэффициент корреляции к -го порядка, то временной ряд имеет циклические колебания периодичностью в к кварталов. Количество сдвинутых рядов должно быть ≤ n/4. Возьмем на один больше. (Рисунок 46)

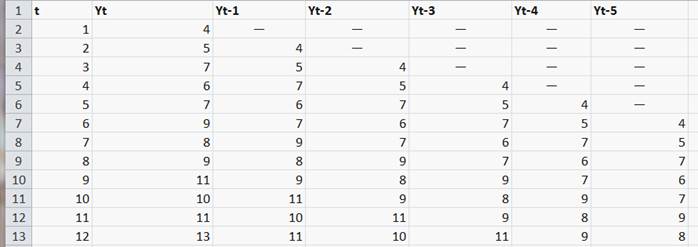
Рисунок 46

Используем: ФОРМУЛЫ, ДРУГИЕ ФУНКЦИИ, СТАТИСТИЧЕСКИЕ, КОРРЕЛ.

Обозначим:

r₁ – коэффициент корреляции между Y_t и Y_t-1

r₂ – коэффициент корреляции между Y_t и Y_t-2

r₃ – коэффициент корреляции между Y_t и Y_t-3 и т. д.

В І2 записываем формулу для нахождения r₁ (Рисунок 47)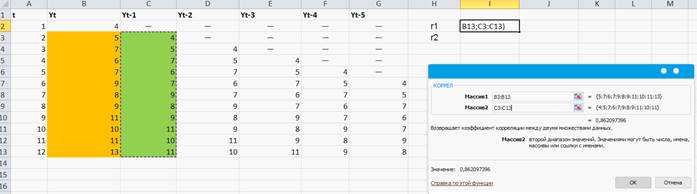

Рисунок 47

После ОК в І3 записываем формулу для нахождения r₂ (Рисунок 48)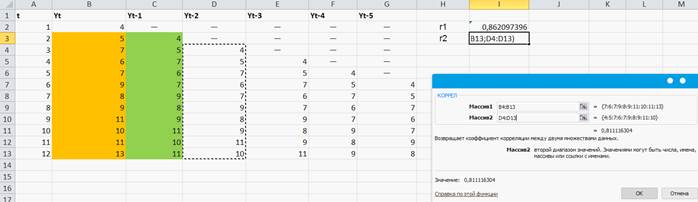

Рисунок 48

Цветами выделены столбцы, между которыми ищем коэффициент корреляции. (Рисунок 49); (Рисунок 50); (Рисунок 51); (Рисунок 52); (Рисунок 53)

Рисунок 49

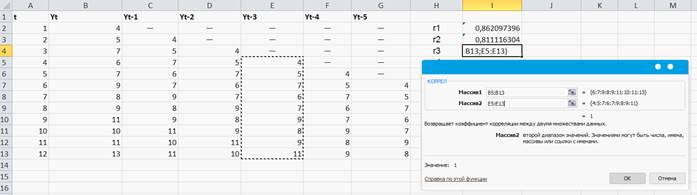
Рисунок 50

Рисунок 51

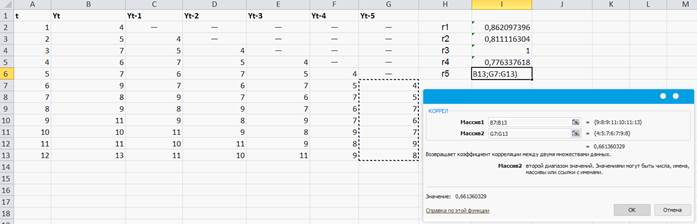
Рисунок 52

Рисунок 53

Так как наибольшее значение имеет коэффициент корреляции 3-го порядка, то временной ряд имеет циклические колебания периодичностью в четыре квартала, т.е. характер ряда повторяется через 3-е периода. Найдем линейную зависимость Y_t от Y_t-4

Yt = a*_Yt-4+b

известным уже методом: выделение исходных данных, затем Вставка, Диаграммы, Точечная (Рисунок 54)

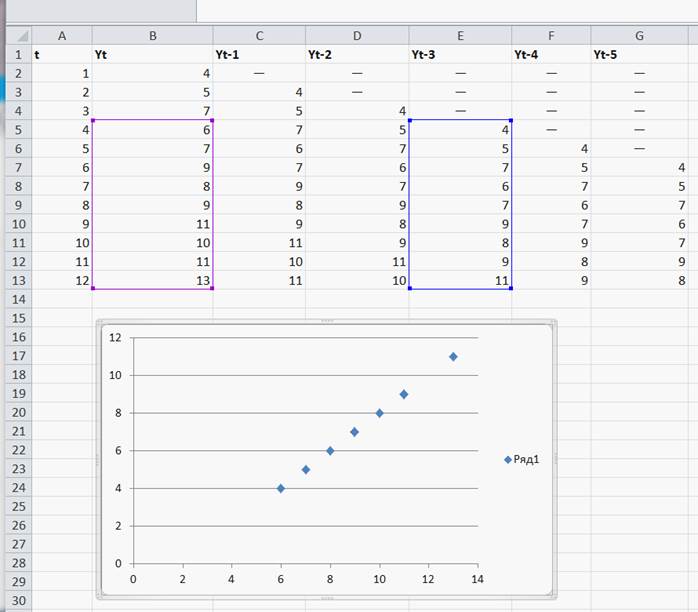
Рисунок 54

После указания правой клавишей мышки на любую точку в появившемся окне выбираем Добавить линию тренда. В новом окне отмечаем параметры линии тренда: Линейная, показать уравнение на диаграмме, поместить на диаграмму величину достоверности аппроксимации R². (Рисунок 55)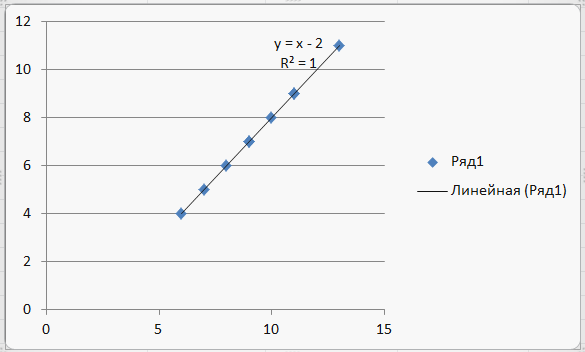

Рисунок 55

Таким образом, искомое уравнение будет:

Y_t = Y_t-4-2

Так как качество полученной связи высокое (R² = 1), то используем ее для прогноза:

Y₁₃ = Y₉-2 = 1*11-2 = 9

Небольшие значения r4 и r5 говорят о том, что линейная связь Y_t (t) слабая. Действительно, выполнив действия, аналогичные выше указанным, получим (Рисунок 56):

Рисунок 56

Небольшое значение R² указывает на то, что линейная зависимость величины потребления электроэнергии Y_t от времени t практически отсутствует.