Кредит-1. Линейная алгебра и аналитическая геометрия.
Практ. зан. № 1Тема № 1 Определители и матрицы.
1. АЗ: [11], №№3.1, 3.3, 3.6, 3.10, 3.12, 3.22, 3.40, 3.44, 3.46, 3.51, 3.76, 3.78, 3.106, 3.159
2. Образцы решения задач:
2.1. Вычислить определитель n-го порядка:
А) приведя к треугольному виду.
б) разложив по элементам какой-либо строки или столбца, по свойству определителей, получим 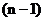 нулей в взятой строке или столбце.
нулей в взятой строке или столбце.

 Решение:
Решение:
а) 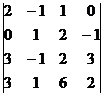 =
= 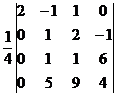 =
= 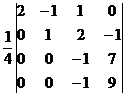
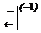 =
= 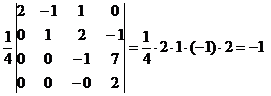
б) 
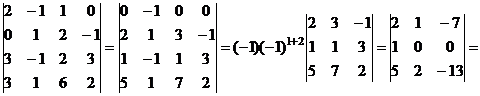
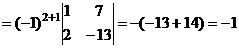

 2.2. Вычислить линейные комбинаций матриц А и В.
2.2. Вычислить линейные комбинаций матриц А и В.
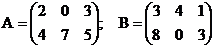 . Найти 5А+2В
. Найти 5А+2В
Решение:
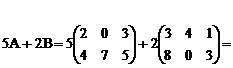
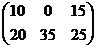 +
+ 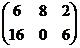 =
= 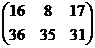
Вычислить АВ и ВА. Проверить равны ли произведения эти матриц.
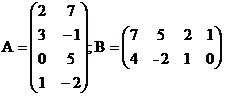
Решение:
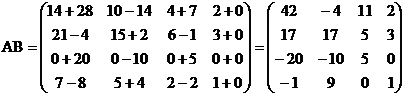
размерность матрицы 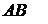 -(4
-(4  4)
4)
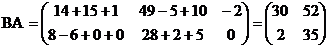
размерность матрицы 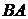 - (2
- (2  2)
2) 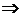
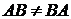
2.4 Найти обратную матрицу А 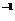 матрицы А
матрицы А
А= 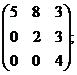
Решение: detA=40 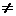 0 матрицы А невырожденная
0 матрицы А невырожденная 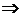 можно найти А
можно найти А 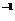
найден A  =(-1)
=(-1) 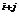 M
M  элементов а
элементов а  .
.
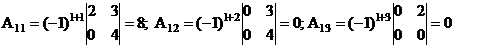
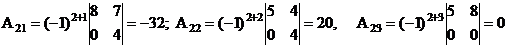
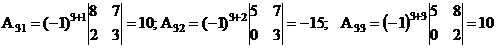

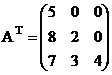 Транспонированная матрица
Транспонированная матрица
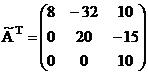 Присоединенная матрица
Присоединенная матрица
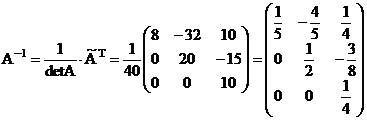
проверим 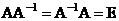
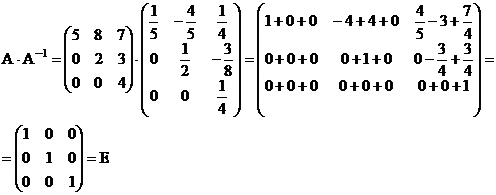
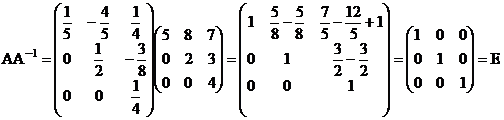
Найти ранг матрицы
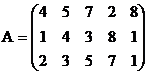
Решение:
а) Методом Гаусса
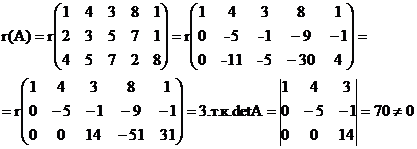
б) методом элементарных преобразований
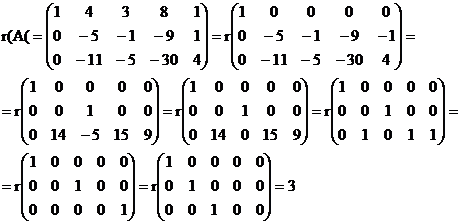
в) методом окаймляющих миноров.
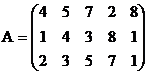
Фиксируем ненулевой минор 2-го порядка 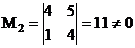
Рассмотрим окаймляющий минор 3-го порядка
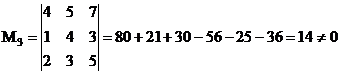
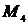 - нельзя составить
- нельзя составить 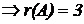
3. ДЗ: [11], №№ 3.2, 3.7, 3.11, 3.13, 3.17, 3.23, 3.45, 3.47, 3.49, 3.77, 3.79, 3.107, 3.160.
Практ. зан. № 2 Тема №1 Система линейных алгебраических уравнений.
1. АЗ: [11], №№3.187, 3.193, 3.208, 3.223.
2.Образцы решения задач.
Проверить совместность системы линейных уравнений
А) методом Гаусса
Б) по теореме Кронекера-Капелли.
Рассмотрим систему трех уравнений с тремя неизвестными
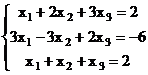
Решение:
где 
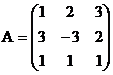
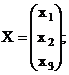
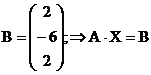 матричная форма системы.
матричная форма системы.
Проверим совместность системы
а) методом Гаусса
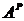
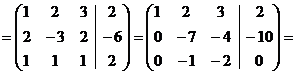
расширенная матрица
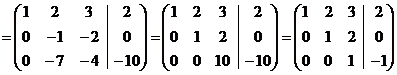
система совместна определитель 3-го порядка отличен от нуля. Система имеет единственное решение и можно найти решения
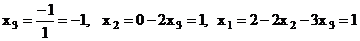
б) по теореме Кронекера-Капелли.
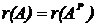
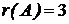 ,
, 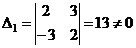
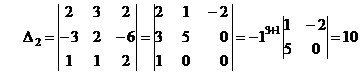
методом окаймляющих миноров

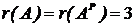 система совместна и имеет единственное решение.
система совместна и имеет единственное решение.
Решить систему уравнений
А) методом Гаусса
Б) методом Крамера
В) матричным методом
Решение:
а) 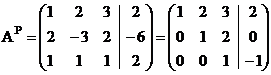
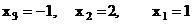
т.е. 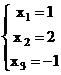
б) методом Крамера
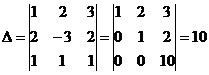
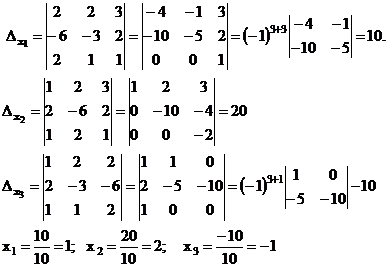
ответ 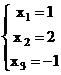
в) матричным методом
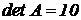 матрица А неврожденная
матрица А неврожденная

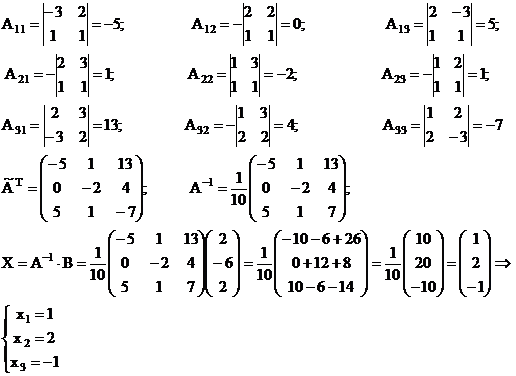
3.ДЗ: [11], №№3.188, 3.194, 3.209, 3.224.
Практ. зан. № 3 Тема №2 Векторная алгебра
1. А.З: [11], №№2.1, 2.8, 2.20, 2.24, 2.27, 2.29, 2.32, 2.36, 2.44,2.50, 2.56, 2.59, 2.63, 2.76, 2.80, 2.92, 2.97, 2.99, 2.104, 2.106.
2.Образцы решения задач
2.1 Определить длину и направляющие косинусы радиуса вектора точки 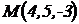 и вектора
и вектора 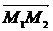 ; если
; если 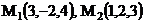
Решение:
а) 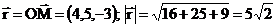
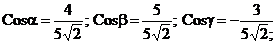
б) 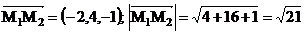
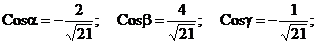
Даны точки 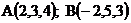 . Найти координаты точки С, делящий отрезок АВ в отношении
. Найти координаты точки С, делящий отрезок АВ в отношении 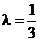 ;
;
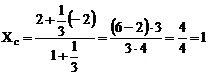
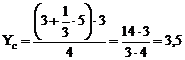

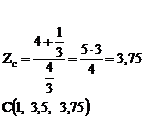
2.2 Найти работу произведенную силой 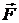 если точки ее приложения, двигаясь прямолинейно, перемещается от точки
если точки ее приложения, двигаясь прямолинейно, перемещается от точки 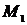 до точки
до точки 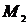 , т.е.
, т.е. 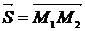 . Работа находится через скалярное произведение вектора
. Работа находится через скалярное произведение вектора 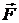 на вектор
на вектор 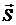 .
.
Решение:
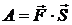
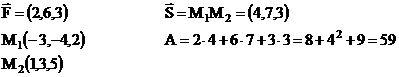
2.3 Даны векторы 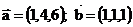
Найти: а) вектор 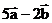
б) модуль 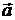
с) 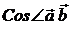
Решение:
а) 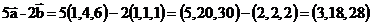
б) 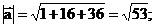
в) 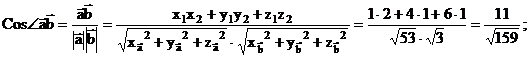
2.4 Найти 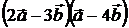 ; если
; если 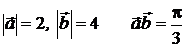 ;
;
Решение:
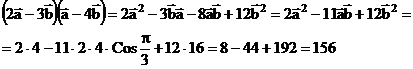
2.5 Доказать, что векторы 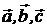 образуют базис и найти координаты вектора
образуют базис и найти координаты вектора 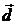 в этом базисе, т.е.
в этом базисе, т.е. 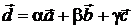 . Для векторов
. Для векторов 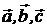 выполняется условие
выполняется условие
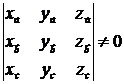
пусть
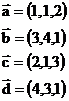 ;
;
Решение:
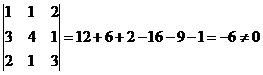
если 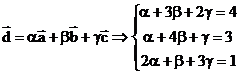 приравниваем X, Y, Z векторов
приравниваем X, Y, Z векторов 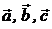 к x, y, z векторам
к x, y, z векторам 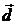 находим
находим 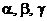


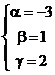
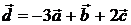
Вычислить объем тетраэдра с вершинами
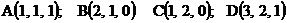
Решение:
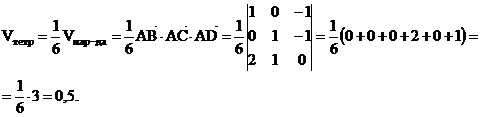
3.Д.З: [11], №№2.2, 2.6, 2.22, 2.23, 2.25, 2.28, 2.30, 2.33, 2.35, 2.45, 2.51, 2.55, 2.58, 2.62, 2.77, 2.81, 2.93, 2.98, 2.103, 2.107.
Практ. зан. № 4 Тема № 3 Плоскость и прямая.
1. АЗ: [11], №№. 2.141,2.143, 2.145, 2.147, 2.153, 2.155, 2.180,2.198.
2. Образцы решения задач
2.1 Даны 3 точки на плоскости А=(1;2), В=(3;3), С=(-2;-3). Найти площадь треугольника с вершинами в этих точках.
Решение:
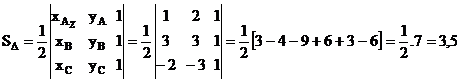
2.2. Даны прямая 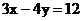 и точка
и точка 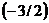 . Найти расстояние от точки до прямой.
. Найти расстояние от точки до прямой.
Решение:
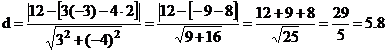
Ответ: 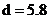
2.3 Дана плоскость 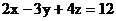 . Привести следующие уравнения плоскости:
. Привести следующие уравнения плоскости:
А) уравнения в отрезок на осях
Б) нормальное уравнение плоскости
В) уравнение плоскости с угловыми коэффициентами
Г) параметрические уравнения плоскости
д) векторное уравнение плоскости
Решение:
а) разделим общее уравнение плоскости на свободный член.
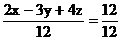 ,
, 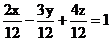
получаем 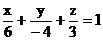 уравнение в отрезках на осях
уравнение в отрезках на осях
б) вычислим длину нормального вектора 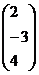 плоскости
плоскости 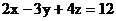 длина =
длина =  =
= 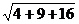 =
= 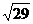
Разделим общее уравнение плоскости на 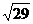 .
.
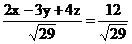 ;
; 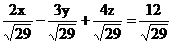
;
получаем 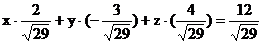 ;
;
нормальное уравнение плоскости
в) выразим 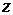 через
через 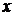 и
и 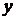 .
.
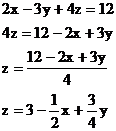
получаем: 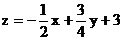 уравнение с угловым коэффициентом.
уравнение с угловым коэффициентом.
г) Запишем следующие уравнения
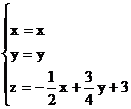 получаем параметры
получаем параметры 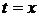 и
и 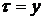
тогда перепишем уравнение
получаем: 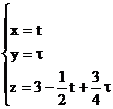 , где
, где 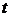 ,
, 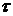 - действительные параметры
- действительные параметры
параметрические уравнения плоскости.
д) запишем параметрические уравнения в векторном виде.
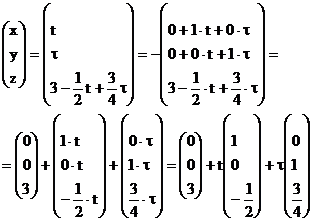
получаем: 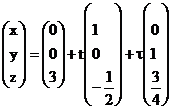
векторное уравнение плоскости.