Вычисление функций на машинах с неограниченными ресурсами.

Как и в случае машин Тьюринга, мы должны указать, как машина с неограниченными регистрами вычисляет частичную функцию f(x1,x2,..., xn) от n аргументов. Рассмотрим набор аргументов (x1,x2,..., xn) и разместим число x1 в регистре R1, число x2 – в регистре R2,..., число xn - в регистре Rn. Все остальные регистры заполнены нулями. Получаем начальную конфигурацию МНР. После окончания работы в регистре R1 должно быть значение функции f(x1,x2,...,xn). Если значение f(x1,x2,..., xn) не определено, то МНР должна работать бесконечно.

72)Вычислимость простейших функций на машинах с неограниченными ресурсами. Теорема. Простейшие функции s(x)=x+1, on(x1,x2,...,xn)=0, In

m(x1,x2,...,xn)=xm вычислимы на МНР. Доказательство. Укажем программы для вычисления данных функций. 1) Функция следования s(x) имеет программу из одной команды S(1). Действительно, если в регистре R1

занесено число x, то МНР выполнит один такт работы, сменит число x в R1 на число x+1 и остановится. 2) Аналогично программа, состоящая из одной команды Z(1), вычисляет нулевую функцию on(x1,x2,...,xn)=0.3) Для функции проектирования In m(x1,x2,...,xn)=xm применяем программу из одной команды T(m,1). МНР выполнит один такт работы, перешлет в регистр R1 число xm и остановится. Теорема доказана. Итак, все простейшие функции из определения частично рекурсивной функции вычислимы на МНР. Далее установим, что все частично рекурсивные функции вычислимы на МНР.

73)Стандартный вид программы. Сложная программа часто содержит другие программы в качестве строительных блоков - подпрограмм. Для правильного взаимодействия этих подпрограмм нужно соблюдать некоторые

правила. Определение. Пусть дана программа для МНР, состоящая из s команд. Будем говорить, что программа имеет стандартный вид, если во всякой команде условного перехода J(m,n,q) данной программы выполняется неравенство q  s + 1. Если программа P не имеет стандартного вида, то в ней найдется команда вида J(m, n, q), где q > s+1. Заменим в программе P эту

команду на команду J(m,n, s + 1). Получим программу P’’, выполняющую точно такое же действие, как и программа P. Действительно, P и P’ отличаются лишь командами J(m, n, q) и J(m,n, s + 1). Однако действие этих команд одинаково: при rm rn нужно перейти к следующей по порядку команде, а при rm = rn остановиться. Определение.Стандартизацией программы I1, I2, …,Is называется замена в данной программе всех команд J(m, n, q) где q > s+1, на команды J(m, n, s + 1). В результате стандартизации из программы P нестандартного вида получим стандартную программу P’ с тем же действием. Используя P’ вместо P, считаем, что все программы, которые мы рассматриваем, стандартны.

74) Соединение программ. Определение. Соединением программ P: I1, I2..., Is и Q: I’1, I’2,..., I’t называется программа из s+t команд вида I1, I2,..., Is, Is+1, Is+2,..., Is+t, где команды Is+1, Is+2,..., Is+t получены из команд I’1, I’2,..., I’t программы Q приращением номеров на число s. При этом каждая команда условного перехода J(m, n, q) из Q заменена на команду вида J(m, n, q+s). Соединение программ P и Q будем обозначать через PQ. Можно соединить программы P, Q, R и получить программу PQR=(PQ)R и т.д.

75) Вставка подпрограммы. Пусть в программе Q имеется подпрограмма P для вычисления функции f (x1,x2,...,xn). В подпрограмме P имеются входные данные (x1,x2,...,xn) и результат вычислений f (x1,x2,...,xn). По определению МНР должны соблюдаться следующие требования. 1. При старте P аргументы (x1,x2,...,xn) обязаны находиться в регистрах R1,...,Rn..

2. После окончания работы подпрограммы P результат f (x1,x2,...,xn) должен содержаться в регистре R. Однако в ходе работы основной программы Q возможно следующее. Настал момент для старта подпрограммы P, которой нужны аргументы x1, x2,..., xn. В данный момент аргументы хранятся в каких-то регистрах Ri1,..., Rin, а не в регистрах R1,..., Rn, как нужно.

Поэтому перед применением подпрограммы P мы должны извлечь аргументы из Ri1,..., Rin и переслать их в регистры R1,..., Rn такой пересылки аргументов выполняется следующее действие. 1) Перед командами из P размещается набор команд T(i1,1),...,T(in,n). Пусть основная программа Q вызвала подпрограмму P и в начало зарезервированных регистров R1,..., Rn скопированы числа x1, x2,..., xn, с которыми начнет работать подпрограмма P. Однако в регистрах Rn+1,...,

R может оставаться «мусор» - произвольные числа, оставшиеся от предыдущей работы Q. По правилам работы МНР в последующих регистрах Rn+1,..., Rk должны быть только одни нули. Поэтому нужно выполнить обнуление этих регистров от мусора, которое осуществляется следующим способом. 2) Выполняется набор команд Z(n+1),..., Z().В итоге в основной программе получается следующий фрагмент T(i1,1)... T(in,n) Z(n+1)... Z() PT(1,i) Вставку данного фрагмента в основную программу обозначаем

через P[i1,..., in i].

76) Вычислимость частично рекурсивных функций на МНР. Если функция f вычислима на некотороймашине с неограниченными регистрами, тоговорим кратко «Функция f МНР вычислима».В предыдущей лекции установлена МНРвычислимость простейших функций. Теперьпроверим, что применение операторовсуперпозиции, примитивной рекурсии иминимизации к МНР вычислимым функциямвырабатывает МНР вычислимые функции. Врезультате получим основной результат -все частично рекурсивные функции вычислимы

на МНР.

77) Оператор суперпозиции. Теорема 1. Пусть функция f получена из

функций h, g1, g2, …, gm с помощью оператора суперпозиции. Если функции h, g1, g2, …, gm МНР вычислимы, то и функция f также МНР вычислима. Доказательство. По условию функции h, g1, g2, …, gm МНР вычислимы. Пусть H, G1, G2, …, Gm- программы, вычисляющие эти функции.

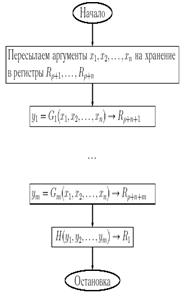
78) Оператор примитивной рекурсии. Теорема 2. Пусть функция f получена с помощью операторапримитивной рекурсии из функций g и h. Если функции g и hМНР вычислимы, то и функция f также МНР вычислима.

Доказательство. По условию функции g и h МНР вычислимы. Пусть G и H программы, вычисляющие эти функции. Выразим кратко процесс вычисления функции f = f(x1, x2,..., xn, y). Сравниваем y с числом 0. Если равенство верно, то вычисляем f(x1, x2,..., xn, 0) = g(x1, x2,..., xn)

и останавливаемся. В противном случае несколько раз применяем программу H для последовательного вычисления чисел f(x1, x2,..., xn, k) при k=0, 1,...y.

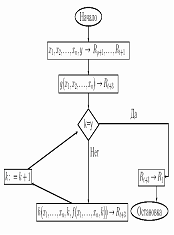
79)Оператор минимизации. Алгоритм вычислений. ► Теорема 3. Пусть функция f получена из функции g с помощью оператора минимизации. Если функция g является МНР вычислимой, то и функция f также МНР

вычислима. Доказательство. Построим программу, вычисляющую функцию f. Пусть G – программа, вычисляющая функцию g. Будем считать, что программа G приведена к стандартному виду. Искомая программа для функции f будет проверять одно за другим следующие равенства: g(x1,x2,...,xn,0)=0,

g(x1,x2,...,xn,1)=0,

...........................

g(x1,x2,...,xn,y)=0, стремясь найти наименьшее k с условием

g(x1,x2,...,xn,k)=0.

80) Программа вычисления. T(1,p+1)

..............

T(n,p+n)

Ip G[p+1, p+2,..., p+n+11]

J(1, p+n+2, q)

S(p+n+1)

J(1, 1, p)

IqT(p+n+1, 1) При этом команда Ip является первой командой

подпрограммы G[p+1, p+2,..., p+n+11].

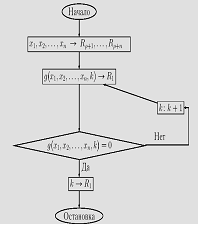
Работа программы Пусть p=max(n+1, p(G)). Распределимпамять: Регистры R1,..., Rp предназначены дляработы подпрограммы G.В регистрах Rp+1,..., Rp+n постояннохранятся аргументы x1,..., xn.В регистр Rp+n+1 будет записыватьсячисло k.В итоге получим искомое число k или машина будет работать бесконечно, что означает, что функция f(x1, x2,..., xn) не существует. Теорема доказана.

81) Нормальные алгорифмы. • Третий вариант формализации понятия алгоритма предложен российским мaтематикомА.А.Марковым.• В этом определении считается, что алгоритмический процесс – это процесс переработки слов некоторого алфавита. Алфавит нормальногоалгорифма A --- это некоторая конечная совокупность символов A = {a1,..., am}. Элементы из A мы будем называть буквами. Из букв алфавита A составляются слова ---

конструктивные объекты, которые поступают на вход и перерабатываются в

алгорифме A. При этом говорят, что A --- алгорифм в алфавите A. Схема нормального алгорифма Рассмотрим две буквы и , которые не входят в алфавит A. Формулой подстановки назовем выражение u  v или выражение u  v, где u и v - произвольные слова в алфавите A. Формула без точки называется простой формулой, а формула с точкой называется заключительной формулой. В обоих случаях формула имеет левую часть u и правую часть v, которые должны быть словами в алфавите A. Знаки  и  могут быть любыми буквами вне алфавита A. Мы могли вместо них

использовать, например, греческие буквы  и .

82) Алгоритм сложения натуральных чисел. Построим нормальныйалгорифм, вычисляющий сумму двух натуральных чисел x и y. Для этого рассмотрим алфавит из трех символов A={0,|,+ }. Число n 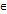N изображаем словом 0||...| в алфавите A. В этом слове n палочек, перед которыми

поставлен символ 0. Искомый нормальный алгорифм A имеет схему из одной

заключительной формулы подстановки u1  v1, где u1 = +0 - слово из

двух букв, а v1 =  - пустое слово. Тем самым схема алгорифма имеет вид

+0 Если нужно вычислить сумму x+y, то подаем на вход алгорифма A ее

изображение, т.е. словоP=0||...|+0||...| Алгоритм A удалит из P подслово +0 и в один шаг переработает входное слово P в выходное слово Q. При этом

Q=0||......|

83) Принцип нормализации Маркова. Сделаем несколько предварительных замечаний. Не все вербальные алгорифмы являются нормальными алгорифмами,такткак вербальные алгорифмы реализуют произвольные преобразования слов, а нормальные алгорифмы ограничены

преобразованиями слов по заданной схеме. Поэтому определение алгоритма по Маркову не будет утверждать о совпадении класса нормальныхалгорифмов и класса вербальных алгорифмов, а будет иметь другую формулировку. Рассмотрим эту формулировку. Пусть задан алфавит A. Добавим к алфавиту A новые буквы. Получим алфавит A1 с условием AA1. Алфавит A1 называется расширением алфавита A. Нормальныйалгорифм в каком-либо расширении A1 алфавита A называется нормальным алгорифмом над алфавитом A. А.А.Марков предложил следующий тезис. Принцип нормализации. Пусть задан произвольный вербальный алгорифм A в алфавите A. Тогда существует расширение A1 алфавита A и нормальныйалгорифм A1 в алфавите A1 с условием: произвольное слово P в алфавите A

перерабатывается нормальнымалгорифмом A1 в тот же самый результат, в который слово P перерабатывается исходным вербальным алгорифмом A.Поэтому принцип нормализации можно рассматривать как способ обозрения всевозможных действий в вербальных алгоритмах. Поскольку эти действия строго заданы, то мы имеем третий вариант определения алгоритма. В результате принятия принципа нормализации мы получили инструмент для доказательства неосуществимости задачи нахождения определенного алгоритма. Доказано, что данная формулировка понятия алгоритма (принцип

нормализации) эквивалентна другим формулировкам понятия алгоритма: тезису Черча, использующему частично рекурсивные функции, и тезису Тьюринга, использующему понятие вычислительной машины. Поэтому еще раз подкрепляется уверенность в том, что мы нашли и выразили в трех формах фундаментальное понятие математики, логики и информатики - понятие алгоритма. При этом частичная рекурсивность, машина Тьюринга, МНР и нормальныйалгорифм - лишь различные формы выражения этого самостоятельного понятия.