Рассмотрим уравнение с одним неизвестным.
Определение. Всякое число (действительное или комплексное) которое, будучи подставлено в уравнение вместо х, обращает уравнение в тождество, называется корнем уравнения.
Пример. Найти корни уравнения 
. Решение: уравнение с одним неизвестным. Корнями являются числа:
; 
; 
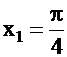Определение. Если уравнение имеет вид 
, где 
- многочлен степени n, то уравнение называется алгебраическим уравнением степени n. Из определения следует, что корни алгебраического уравнения те же, что и многочлена .
Возникает вопрос – всякое ли уравнение имеет корни?
В случае если уравнение не алгебраическое, то оно может не иметь ни одного корня, ни действительного, ни комплексного, например: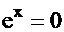 
.
Но в случае алгебраического уравнения ответ дает основная теорема алгебры.
Теорема 2. (Основная теорема алгебры) Всякая целая рациональная функция 
имеет, по крайней мере, один корень действительный или комплексный.
Доказательство в курсе высшей алгебры, но пользуясь этой теоремой можно доказать следующую теорему:
Теорема 3. Всякий многочлен n –й степени разлагается на n линейных множителей вида 
и множитель равный коэффициенту при 
.
Доказательство: Пусть - многочлен степени n.
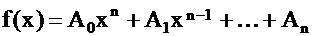
В силу основной теоремы этот многочлен имеет хотя бы один корень, обозначим его через 
.Тогда в силу следствия теоремы Безу
,
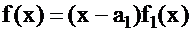где 
- многочлен 
- й степени; - также имеет корень, обозначим его через 
, тогда
,
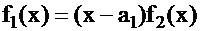- многочлен 
- й степени, который также имеет корень и т.д. Получим: 
, где 
- многочлен нулевой степени, 
- коэффициент при , получим:
.
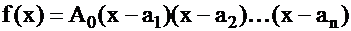Замечание. Многочлен n – й степени не может иметь более чем n различных корней.
Пример. Разложить на множители многочлен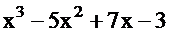 
.
Решение: Найдем корни путем подбора.
Поделим заданный многочлен на 
.
Пример 2.Разложить на множители многочлен 
.
Решение: Найдем корни путем подбора.
Поделим заданный многочлен на .
2. Кратные корни многочлена.
Если в разложении многочлена n – й степени на линейные множители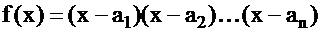 
некоторые окажутся одинаковыми, то их можно объединить и тогда разложение будет иметь вид:
при этом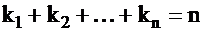 
и корень называется корнем кратности 
; корень называется корнем кратности 
, и т.д.
Пример. Многочлен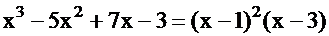 
имеет корень 
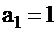кратности 2, второй корень 
- кратности 1.
Замечание. Все, что говорилось о корнях многочлена
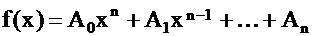
можно сформулировать в терминах корней алгебраического уравнения 
.
3. Разложение многочлена на множители в случае комплексных корней.
Теорема. Если многочлен 
с действительными коэффициентами имеет комплексный корень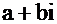 
, то он имеет и сопряженный корень 
.
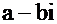Доказательство: Подставим в многочлен вместо х, 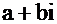, возведем в степень и соберем отдельно члены, содержащие i и не содержащие 
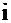, получим, 
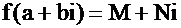, где М и N – выражения, не содержащие i. Поскольку, 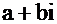- корень многочлена, то 
, откуда М=0 и N=0. Подставим в многочлен вместо х выражение 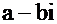, тогда возводя в степень и собирая элементы, содержащие i и не содержащие i, получим 
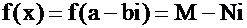, так как М=0 и N =0, то 
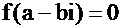, то есть 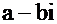- есть корень многочлена.
Вывод. В разложении 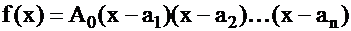комплексные корни входят попарно-сопряженными.
Перемножив линейные множители, соответствующие паре комплексно-сопряженных корней получим трехчлен второй степени с действительными коэффициентами
,
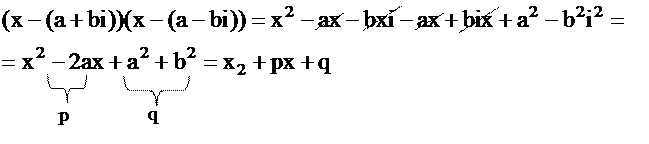где 
и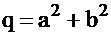 
действительные числа.
Например:
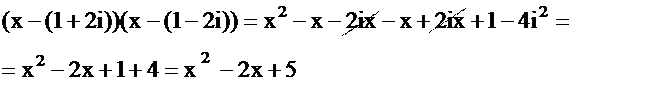
Если число 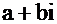является корнем кратности k, то сопряженное число должно являться корнем той же кратности k.
при этом 
.