Рассмотрим некоторую систему, которая может находиться в одном из состояний 
. В моменты t, равные 0, 1, 2, 3,… система переходит из одного состояния в другое. Определим случайные величины 
, соответствующие состояниям системы в моменты t=0, 1, 2,…. 
, если система в момент t находится в состоянии 
.
Вероятность
(9.1)
называется вероятностью перехода из состояния i в состояние j за один шаг. Марковская цепь называется однородной, если величины 
не зависят от t (т.е. 
при всех i,j=1,…,n). В дальнейшем рассматриваются только такие цепи и величина (9.1) обозначается через 
. Матрица переходов за один шаг определяется соотношением
(9.2)
Для этой матрицы
(9.3)
Вектор начальных вероятностей 
, где 
.
Часто Марковскую цепь удобно задавать при помощи графа переходов. При построении такого графа каждому состоянию ставится в соответствие вершина. Если из состояния xi система переходит в состояние xj с ненулевой вероятностью , то из вершины, соответствующей xi, проводится стрелка в вершину xj, помечаемая величиной ; если 
, то стрелку не проводят.
Вероятности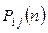 
, определяемые равенством
,
называют вероятностями перехода за n шагов.
Матрица 
называется матрицей перехода за n шагов. Справедливо равенство
(9.4)
ЗАДАЧИ
1. Даны матрицы:
Какие из них могут задавать вероятности перехода Марковской цепи, какие не могут? Почему?
2. В зависимости от атмосферных условий связь между двумя станциями может быть хорошей, удовлетворительной или плохой (состояния А1, А2, А3). Известно, что если в течение данного часа связь хорошая, то в течение следующего часа с вероятностью 0,6 связь остается хорошей, а с вероятностью 0,3 становится удовлетворительной. Если связь в течение часа удовлетворительная, то в течение следующего часа она с вероятностью 0,4 становится хорошей и с вероятностью 0,1 плохой. Если же связь была плохая, то в следующем часу она с равной вероятностью может стать хорошей, удовлетворительной или плохой. Считая состояния связи Марковской цепью, построить ее матрицу переходов. Сделать тоже для двух состояний связи - плохая, неплохая, понимая под последним состоянием - хорошая или удовлетворительная.
3. На окружности расположены шесть точек 
равноотстоящих друг от друга. Частица движется из точки в точку следующим образом. Из данной точки она перемещается в одну из ближайших соседних точек с вероятностью 1/4 или диаметрально противоположную точку с вероятностью 1/2. Выписать матрицу вероятностей перехода и построить граф, соответствующий этой матрице.
4. В мастерскую для ремонта поступают моторы двух типов. Ремонт мотора типа М1 требует одного дня, типа М2 - двух дней. Каждое утро вероятность поступления на ремонт мотора типа М1 равна 1/2 и типа М2 - 1/3. Если день занят ремонтом мотора М2, то отказывают любому заказу. Составить матрицу переходов в двух случаях: при возможности выбора заказа предпочтение отдается: а) ремонту мотора М2, б) ремонту мотора М1.
5. В учениях участвуют два корабля, которые одновременно производят выстрелы друг в друга через равные промежутки времени. При каждом обмене выстрелами корабль А поражает выстрелами корабль В с вероятность 1/2, а корабль В поражает корабль А с вероятностью 3/8. Предполагается, что при любом попадании корабль выходит из строя. Найти матрицу вероятностей перехода, если состояниями цепи являются комбинации кораблей, оставшихся в строю: Е1 - оба корабля в строю, Е2 - в строю корабль А, Е3 - в строю корабль В, Е4 - оба корабля поражены.
6. Пусть Е1, Е2, Е3- возможные состояния системы и Р - матрица вероятностей перехода из состояния в состояние за один шаг:
Найти матрицу переходов за два и три шага.
7. Вероятности перехода за один шаг в цепи Маркова заданы матрицей:
. Требуется построить граф переходов. Найти матрицу переходов за два шага.
8. Погода на некотором острове бывает дождливой (Д) и сухой (С). Вероятности ежедневных изменений погоды заданы матрицей:
а) если сегодня дождь, то какова вероятность, что послезавтра будет сухо?
б) если в среду ожидается дождливая погода, с вероятностью 0,3, то какова вероятность того, что она будет дождливой в ближайшую пятницу?
9. Марковская цепь с двумя состояниями A1 и А2 задана матрицей переходов:
а) найти вероятность перехода из состояния А1 в А2 за два шага;
б) найти вероятность того, что через два шага цепь будет в состоянии А2, если сначала цепь находилась с вероятностью 1/2 в состоянии А2.
10. Матрица вероятностей перехода цепи Маркова имеет вид:
Распределение по состояниям в момент времени t=0 определяется вектором Р0= (0,7;0,2;0,1). Найти:
а) распределение по состояниям в момент времени t =2;
б) вероятность того, что в момент времени t =0,1,2,3 состояниями цепи будут соответственно А1, А2, Аз;
в) стационарное распределение.
11. Для цепи, заданной матрицей вероятностей перехода
. Найти стационарное распределение.
12. Доказать, что цепи, задаваемые переходными матрицами вида:
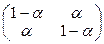при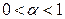 
имеют одно и тоже стационарное распределение.
13. Аппаратура может находиться в рабочем состоянии (А1), в ожидании ремонта (А2), в ремонте (А3). Вероятности перехода из состояния в состояние в течение суток даны в матрице:
В случае эксплуатации станции фирма получает ежедневно 500 руб.; при простое платит неустойку 50 руб. в сутки, сутки ремонта стоят 100 руб. Каков среднесуточный доход фирмы?
14. 60% детей выпускников СибГУТИ учатся в СибГУТИ. 30% в других вузах и 10% в вузы не поступают. Дети, родители которых окончили другие вузы, учатся в СибГУТИ - 20%, в других вузах -70%, нигде не учатся - 10%. Для детей, родители которых не имеют высшего образования, эти проценты соответственно, 10, 40, 50. Какова вероятность, что в СибГУТИ будут учиться: а) сын выпускника СибГУТИ; б) его внук; в) его достаточно далекий потомок?
15. В стране Ландии климат весьма изменчив. Здесь никогда не бывает двух ясных дней подряд. Если сегодня ясно, то завтра с одинаковой вероятностью пойдет дождь или снег. Если сегодня дождь (или снег), то с вероятностью 1/2 погода не изменится. Если же она изменится, то в половине случаев снег заменяется дождем или наоборот и лишь в половине случаев на следующий день будет ясная погода. Требуется:
а) принимая в качестве состояний цепи различные виды погоды Д, Я, С, выписать матрицу перехода;
б) построить граф, соответствующий этой матрице;
в) определить вероятности хорошей погоды через три дня после дождя;
г) найти предельные вероятности.
16. Электрон может находиться на одной из счетного множества орбит в зависимости от энергии. Переход с i -й орбиты на j - происходит за одну секунду с вероятностью:
Найти вероятность перехода за две секунды и постоянные сi.
МАРКОВСКИЕ ПРОЦЕССЫ
Случайный процесс 
называется марковским, если для любого момента времени t0 при зафиксированном значении 
случайные величины 
, не зависят от величины 
, s < t0. Неформально это означает, что поведение системы, описываемой случайной величиной , после какого-либо момента времени t0 зависит только от величины 
и не зависит от при s < t0.
Пусть процесс может принимать только конечное или счетное число значений из множества целых неотрицательных чисел 
. Через 
обозначим вероятность того, что система, находящаяся в момент s в состоянии i окажется в момент времени t в состоянии j:
(10.1)
Марковский процесс называется однородным, если при всех s, t вероятность 
зависит только от разности t – s. Другими словами, при любом D и всех i, j, s, t выполняется равенство
В дальнейшем будут рассматриваться только однородные марковским процессы и через 
будем обозначать вероятность того, что система за время t перейдет из состояния i в j:
(10.2)
Для описания марковского процесса с состояниями 0, 1, 2,…, n, часто используют вероятности состояний 
:
(10.3)
, т.е. 
- вероятность того, что система, описываемая марковским процессом в момент времени t, находится в состоянии k. Через 
, обозначим начальное распределение вероятностей, т.е.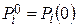 
.
Величины (10.2) и (10.3) связаны равенствами:
(10.4)
Здесь по определению
(10.5)
Ниже рассматриваются только процессы, у которых переходные вероятности удовлетворяют следующим условиям:
(10.6)
Здесь 
Величина 
называется плотностью или интенсивностью выхода из i; 
называется плотностью или интенсивностью перехода из i в j; по определению,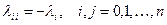 
.
Для марковского процесса с конечным числом состояний при выполнении условий (10.6) справедливы дифференциальные уравнения:
(10.7)
Начальные данные для системы уравнений (10.7) задаются неравенствами 
.
При составлении дифференциальных уравнений (10.7) удобно пользоваться графом состояний системы, на котором состояния процесса изображены кружками. Если плотность перехода из состояния i в j не нулевая, то на графе из i в j ведет стрелка, над которой приведено значение . Пример такого графа приведен на рисунке 6. У системы, описываемой эти марковским процессом, три состояния (0,1,2), причем
.
Рисунок 6
Уравнения по графу состояний записываются по следующему правилу: в левой части стоит производная 
, а в правой части стоит столько членов, сколько стрелок входит и выходит из состояния j. Если стрелка ведет в j -ое состояние из i -го, то ей соответствует слагаемое 
, если стрелка из j -го состояния в k -ое, то ей соответствует слагаемое 
. Например, для графа на рисунке 1 получаем систему уравнений
(10.8)
Число уравнений системы может быть уменьшено на 1, если воспользоваться условием нормированности вероятностей: для любого t
(10.9)
Например, из системы (10.8) можно убрать последнее уравнение, а 
найти из равенства 
.
ЗАДАЧИ
1. Некто купил радиоприемник с двумя запасными предохранителями. В процессе работы приемника используется один предохранитель; перегоревший предохранитель заменяется на новый. Вероятность того, что предохранитель сгорит в промежутке времени 
, равна 
при 
час-1.
Найти вероятность того, что этих предохранителей не хватит на 400 часов работы.
Решение. Введем состояния рассматриваемой системы: 0 – все предохранители исправны, 1 – один предохранитель сгорел, 2 – и 3 – сгорели два и три предохранители, соответственно. По условию задачи плотность перехода из состояния i в (i+1) равна 0,01 час-1 при i= 0,1,2, т.е. 
. Требуется найти вероятность того, что сгорят все предохранители менее, чем за 400 часов работы, т.е. 
. Для этого сначала нарисуем граф переходов рассматриваемой системы:
Рисунок 7
Затем по этому графу составим систему дифференциальных уравнений вида (1.7)
Т.к. в начальный момент (t=0) все предохранители целые, т.е. система находится в состоянии 0, то для системы уравнений получаем следующие начальные данные:
Решая первое уравнение, получаем 
. Подставляя это решение во второе уравнение, получаем 
, затем, подставляя в третье и четвертое, находим:
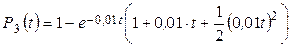
Из последней формулы находим 
.
2. В четырехэтажном здании есть пассажирский лифт. Если через i, i=1, 2, 3, 4 обозначить состояние «лифт находится на i-ом этаже», то граф переходов выглядит так:
Рисунок 8
По этому графу определить, какова интенсивность перехода лифта с первого этажа на 3-й? с 4-го на 3-й? Какова интенсивность выхода из 3-го состояния? Чему равно 
?
3. Для систем, заданных графами на рисунке, надо составить систему дифференциальных уравнений вида (1.7) для вероятностей 
При этом считать, что в начальный момент (t=0) система находится в нулевом состоянии.
а) б)
в) г)
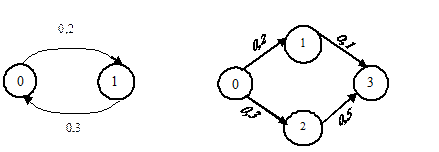
Рисунок 9
4. Решить задачу 1.1 при условии, что даны не два запасных предохранителя, а один.
5. Прибор содержит две идентичных блока. Вероятность выхода блока из строя в промежуток времени равна 
с 
час-1. В комплекте поставки содержится один запасной блок. Какова вероятность того, что прибор не выйдет из строя в течение 20 часов работы, если перегоревший блок немедленно заменяется на резервный?
Указание. Вероятность того, что один из двух блоков выйдет из строя в течение времени равна 
при 
.
6. В читальном зале имеются две используемые ртутные лампы и еще одна запасная. Если одна из двух ламп перегорает, то она заменяется на запасную. В случае, если в зале перегорают обе лампы (и нет запасной), зал закрывают. Какова вероятность того, что читальный зал не закроют в течение 100 часов работы, если вероятность того, что работающая лампа перегорит в интервале времени равна при 
?
7. Для того чтобы перевезти 120 студентов на практику, заказали три 60-ти местных автобуса. Известно, что на весь путь потребуется 5 часов и вероятность того, что автобус выйдет из строя в интервале времени равна с 
час-1. Какова вероятность того, что все студенты будут привезены без задержек? (все автобусы едут в колонне и в случае необходимости студенты могут пересаживаться из автобуса в другие).
8. Некто собрался в поездку на легковой машине. Продолжительность пути - 10 часов. Известно, что вероятность прокола в дороге колеса за время равна с час-1. Какова вероятность того, что во время поездки не придется заклеивать камеру колеса, если в машине есть одно запасное колесо?
9. Пусть имеется система, состоящая из одного основного элемента и n тождественных ему элементов, находящихся в резерве. Основной элемент находится под нагрузкой и в промежутке времени может выйти из строя с вероятностью . В этом случае основной элемент сразу заменяется на один из резервных. Система отказывает тогда, когда выходят из строя все элементы - основной и n резервных. Найти вероятность того, что система проработает время t.
10. Ливень космических частиц вызван попаданием в начальный момент времени в атмосферу одной частицы. Определить вероятность того, что спустя время t будет n частиц, если каждая частица в промежутке времени с вероятностью может вызвать возникновение новой частицы, имеющей практически ту же самую вероятность «размножения».