1. Метод сжимающих отображений.
Df. Пусть M – некоторое подмножество Банохового пространства B. Оператор A, определенный на множестве М, сжимает М, если: 1.  ; 2. Оператор А сжимает М, т.е.
; 2. Оператор А сжимает М, т.е.  , такое, что имеет место оценка:
, такое, что имеет место оценка:  .
.
Геометрический смысл: Оператор А уменьшает расстояние между точками.
Теорема (принцип сжатых отображений) Пусть М – замкнутое, ограниченное мн-во в B, и пусть А сжимает M  имеет решение
имеет решение  и это решение единственно.
и это решение единственно.
2. Лемма Адамара
Для дифференцируемой функции g(x) одной переменной справедлива формула конечных приращений Лагранжа, а именно:  .
.
Df. Область D в пространстве  называется выпуклой, если вместе с любыми двумя точками, принадлежащими этой области, она содержит отрезок, их соединяющий.
называется выпуклой, если вместе с любыми двумя точками, принадлежащими этой области, она содержит отрезок, их соединяющий.
Рассмотрим  . Имеет место следующая лемма.
. Имеет место следующая лемма.
Лемма 1: Пусть функция  непрерывно дифференцируема в выпуклой области.
непрерывно дифференцируема в выпуклой области.  . Если любые точки
. Если любые точки  , то справедливо следующее равенство:
, то справедливо следующее равенство:
 , где
, где 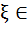 отрезку
отрезку  .
.
Лемма 2: Если условия Леммы 1 выполняются, то  , где
, где  – непрерывна по совокупности переменных
– непрерывна по совокупности переменных 
Лемма 3: Пусть вектор-функция  , непрерывно дифференцируема в замкнутой ограниченной выпуклой области D, тогда для любых элементов
, непрерывно дифференцируема в замкнутой ограниченной выпуклой области D, тогда для любых элементов 
 , где через
, где через 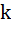 обозначен по всем точкам
обозначен по всем точкам 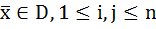 , по
, по  .
.
Лемма Адамара:  и
и  имеет непрерывные частные производные до n-го порядка включительно в области D. Тогда
имеет непрерывные частные производные до n-го порядка включительно в области D. Тогда  имеющие частные производные по
имеющие частные производные по 
 и такие, что
и такие, что  .
.
Вопрос 11. Доказательство теоремы существования и единственности (общий случай). Комментарий к основной теореме.
 =
=  (
( ,t),
,t),  =
= 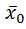 (*)
(*)
Решение задачи Коши (*) эквивалентно системе интегральных уравнений:
 (1)
(1)
 =
= 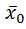 +
+  (2)
(2)
Лемма Если  (t) – непрерывная дифференцируемая функция при t
(t) – непрерывная дифференцируемая функция при t  [a;b], то имеет место
[a;b], то имеет место  ≤
≤  (3)
(3)
Д-во:
 ≤
≤  ≤ [ но по определению нормой вектора
≤ [ но по определению нормой вектора 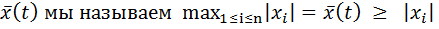 ] ≤
] ≤ 

Применим к (*) принцип сжатых отображений: образуем параллелепипед  ≤a, ||
≤a, ||  ||≤
||≤  } целиком содеращийся в (n-1)- одномерной области G
} целиком содеращийся в (n-1)- одномерной области G
П 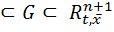
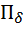 ={
={  ≤
≤  ≤
≤  a; ||
a; ||  ||≤
||≤  }
}
 =
= 
 =
= 
Рассмотрим банахово пространство B. У нас можно отождествить B с С[t0-  ; t0+
; t0+  ], т.е. с простраством непрерывных на отрезке |t-t0|≤
], т.е. с простраством непрерывных на отрезке |t-t0|≤  функций
функций  вещественно значных, обладающих следующей нормой:
вещественно значных, обладающих следующей нормой:
||  ||C=
||C= 
В качестве множества М выберем множество вектор-фукций  из B, для которых ||
из B, для которых ||  ||≤b (4)
||≤b (4)
Множество М будет замкнуто, так как если  =
= 
 и кроме того поскольку для
и кроме того поскольку для  имеет место (4), то
имеет место (4), то 
Нам необходимо преверить, что оператор А, определенный (2) сдимаеи мно-во М, если  достаточно мало
достаточно мало
1)  x(t)
x(t)  , доказать А(
, доказать А( )
) 
А( )
)  = С[t0-
= С[t0-  ; t0+
; t0+  ]
]
|| А( )
) 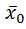 ||=
||=  ≤(используется (3)) ≤
≤(используется (3)) ≤  ≤K0
≤K0  =K0|t-t0|=K0
=K0|t-t0|=K0  ≤b
≤b 
 ≤
≤ 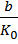 (5)
(5)
 A: M
A: M 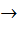 М
М
Покажем, что если  достаточно мало, то
достаточно мало, то
2)|| А( )- А(
)- А( )||C≤q||
)||C≤q||  ||C
||C
Где 0≤q≤1, а  - любые элементы множества М
- любые элементы множества М
|| А( )- А(
)- А( )||=[в силу(2)]=
)||=[в силу(2)]= 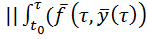 -
-  ||≤K1n||
||≤K1n||  ||C
||C  =K1n||
=K1n||  ||
||  ;
;  ≤
≤  (7)
(7)
Если  , то оператор А сжимает М. Применяя принцип сжатых отображений к (1) получим, что это урав-е имеет непрер. решение
, то оператор А сжимает М. Применяя принцип сжатых отображений к (1) получим, что это урав-е имеет непрер. решение  на оторезке |t-t0|
на оторезке |t-t0|  и при том единственное. Решения * и системы инт. уравнения (1,2) эквивалентны.
и при том единственное. Решения * и системы инт. уравнения (1,2) эквивалентны.
Комментарии к основной теореме


Комментарий 2: Непрерывность правой части 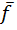 достаточна для существования решения.
достаточна для существования решения.
Теорема Пеано
Пусть  и (t0;
и (t0; 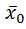 )
)  тогда решение (1),(2) существуют на I=[t0-
тогда решение (1),(2) существуют на I=[t0-  ; t0+
; t0+  ]
]  .
.
Комментарий 3: Для единственности решения непрерывности правой части 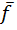 недостаточно.
недостаточно.
Вопрос 12. Теорема (  и! для ДУ n-ого порядка)
и! для ДУ n-ого порядка)
Пусть имеется ДУ n-ого порядка  (1) разрешенное отн-но старшей производной
(1) разрешенное отн-но старшей производной  (2)
(2)
Задача Коши для этого: найти решения ДУ (1), удовлетворяющие (2): 
Теорема ( и! для ДУ n-ого порядка)
и! для ДУ n-ого порядка)
Пусть  от n- переменных непрерывных вместе со своими частными производными
от n- переменных непрерывных вместе со своими частными производными  в области G, где
в области G, где  и пусть точка
и пусть точка  , тогда решение задачи Коши
, тогда решение задачи Коши 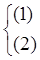 :
:
1)  и! на некотором интервале
и! на некотором интервале 
2)! на 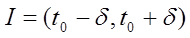
Д-во: (n=2)
 (3)
(3)  (4). Пусть
(4). Пусть  определены и непрерывны
определены и непрерывны  и точка
и точка 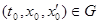 тогда решение задачи Коши
тогда решение задачи Коши 
 и! на
и! на 
Отметим, что для док-ва применяем метод построения приближенной системы, введем замену  (5)
(5)  (6).
(6).  (7)
(7)
Используя (5) мы переписали  , в виде
, в виде  . Система (6) подобна (3).
. Система (6) подобна (3).  выполняется все условия теоремы
выполняется все условия теоремы  и!
и!  решение будет
решение будет  и будет!. Поскольку с помощью замены (5)
и будет!. Поскольку с помощью замены (5)  подобна
подобна 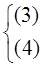 , то отсюда мы получаем заключение нашей теоремы. (Док-но)
, то отсюда мы получаем заключение нашей теоремы. (Док-но)
Вопрос 13. Продолжение решений. Гладкость решения
 (*)
(*)
Продолжение решения.
Пусть  есть решение (*) определенно I=
есть решение (*) определенно I=  это решение может быть продолжено вообще говорят на большем интервале
это решение может быть продолжено вообще говорят на большем интервале  и
и  .
.
Решение называется неограниченное продолжение, если его можно продолжить на всю ось, т.е.  (
(

 ). Пусть Г-граница области G.
). Пусть Г-граница области G.
Df: решение  , которое
, которое  называется продолжением вперед до границы Г, если существует его продолжение
называется продолжением вперед до границы Г, если существует его продолжение  определены на конечном интервале
определены на конечном интервале  и такое что точки вида
и такое что точки вида  при t близким
при t близким  не содержащие ни в каком множестве
не содержащие ни в каком множестве  . Аналогичное определение продолжения решения назад вплоть до границы Г.
. Аналогичное определение продолжения решения назад вплоть до границы Г.
Теорема (о продолжение решения): пусть для системы (*) в области  выполняются условия основной теоремы существования и!, тогда всякое решение этой задачи (*) продолжение вперед (назад) либо не ограничено, либо вплоть до границы Г и это продолжение!.
выполняются условия основной теоремы существования и!, тогда всякое решение этой задачи (*) продолжение вперед (назад) либо не ограничено, либо вплоть до границы Г и это продолжение!.
Д-во: поясним понятие продолжения до границы Г для уравнения: 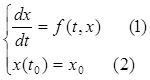 ; пусть y(t) описанное ранние продолжение решения x(t) определенное при
; пусть y(t) описанное ранние продолжение решения x(t) определенное при  . Существует 3-и логических возможностей:
. Существует 3-и логических возможностей:
1)  и конечен
и конечен
2) 
3) не 
Случай 1: точка  и предельная точка интегральной кривой лежит на границе. Этот случай реализован для уравнения, где
и предельная точка интегральной кривой лежит на границе. Этот случай реализован для уравнения, где 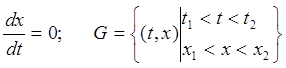
Случай 2: реализация для уравнения  ;
; 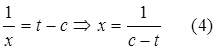 ;
;  (6);
(6);  (7). Пусть x(f)=1, тогда t=2 решение превращается в бесконечность.
(7). Пусть x(f)=1, тогда t=2 решение превращается в бесконечность.
Случай 3: реализация для уравнения  (8);
(8);  (9).
(9).
(8) – одно из частных решений (9).Пусть определим G. G= 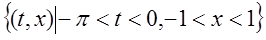 .
. 
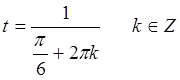 ,
,  , а множество предельной точки интегральной кривой задается отрезком t≤0, -1≤x<1
, а множество предельной точки интегральной кривой задается отрезком t≤0, -1≤x<1
Гладкость решения.
Рассмотрим систему из n-уравнений  (1)
(1)
Теорема: пусть F  обладает непрерывной производной по всем переменным до порядка p≥1 включительно, тогда всякое решение системы (1) имеет непрерывную производную до порядка (p+1)
обладает непрерывной производной по всем переменным до порядка p≥1 включительно, тогда всякое решение системы (1) имеет непрерывную производную до порядка (p+1) 
Д-во: геометрическая теорема утверждает, что чем более гладкие правые части, тем более гладким будет ее решение. Пусть p=1 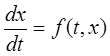 ;
;  - непрерывны
- непрерывны
X(t) – непрерывно дифференцируемо. Подставим  (2);
(2);
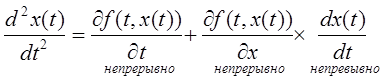 (3)
(3) 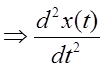 - непрерывно
- непрерывно  функция (2) дифференцируема.
функция (2) дифференцируема.
Вывод: 1. По внешнему виду уравнения можно узнать есть ли решение, установить механизм решения.
Вопрос 14. Зависимость решения от параметра и начального условия.
ДУ описывая физические процессы всегда содержит некоторый параметр. Этот параметр в реальных задачах никогда не могут быть изменены абсолютно точно. Т.е. всегда измеряются с некоторой погрешностью, так что сами ДУ известны лишь с некоторой степенью точности, поэтому для того чтобы уравнения могли описывать реальные процессы необходимо, чтобы их решение мало менялось при малых значениях параметра.
Теорема (о непрерывной зависимости решений от параметра)
 (1);
(1);  (2)
(2)
Найдем решение (1) удовлетворяющие (2), если  определены и непрерывны в
определены и непрерывны в 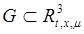 и точка
и точка  . Задача Коши
. Задача Коши 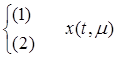 являются непрерывными по совокупности переменных
являются непрерывными по совокупности переменных 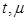 в некоторой области
в некоторой области  ;
;  . Интегрируя кривые уравнения (1) образующих семейство кривых проходящих через точку
. Интегрируя кривые уравнения (1) образующих семейство кривых проходящих через точку  .
.
Теорема утверждает, что интегральные кривые отвечающие близким значение параметра близки
Д-во: сведем задачу Коши  к решению эквивалентное ей интегральные уравнения
к решению эквивалентное ей интегральные уравнения
 (3); x=A(x) (4).
(3); x=A(x) (4).
Возьмем параллелепипед 
 , т.к. множество замкнутое и функция непрерывная. Найдем
, т.к. множество замкнутое и функция непрерывная. Найдем 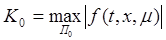 ;
; 
Применяя к уравнению (4) принцип сжимающих отображений. В качестве пространства B возьмем пространство функции  в область
в область 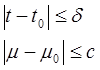 где
где 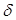 выберем ниже с нормой
выберем ниже с нормой 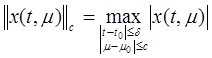 . В качестве множества
. В качестве множества  возьмем функцию
возьмем функцию  , которая удовлетворяет условию
, которая удовлетворяет условию 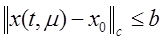 .
.
Заметим, что если функция  , то
, то 
 при
при 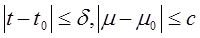 , то теореме (о непрерывной зависимости решений от параметра) мы получим
, то теореме (о непрерывной зависимости решений от параметра) мы получим  .
.
Далее дословно повторяя док-во основной теоремы получаем, что при 
Получаем, что оператор A сжимает множество  . Откуда и вытекает заключение теоремы.
. Откуда и вытекает заключение теоремы.
Замечание: точно так же формулируется и доказывается теорема о непрерывной зависимости решений от параметра для системы.
 (5);
(5);  (6). Если
(6). Если  ,
,  определены и непрерывны в
определены и непрерывны в  ,
, 
Вопрос 15. Уравнения 1-ого порядка, не разрешённые относительно производным
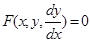 (1), где F-заданная ф.-ция, которая действительна и непрерывна в окрестн. точки (x,y,p)∊DᴄR3.
(1), где F-заданная ф.-ция, которая действительна и непрерывна в окрестн. точки (x,y,p)∊DᴄR3.  (2).
(2).  -определяет в 3ёх-мерном пространстве поверхность. Теор.: Пусть выполн. условие
-определяет в 3ёх-мерном пространстве поверхность. Теор.: Пусть выполн. условие 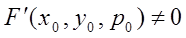 (3). И имеется задача Коши:
(3). И имеется задача Коши:  (1),
(1),  (2), p0-корень ур.-ния
(2), p0-корень ур.-ния  (4).Тогда решение задачи Коши Ǝ и единственно. Д.-ва: В силу теор. о неявной ф.-ции из ур.-ния
(4).Тогда решение задачи Коши Ǝ и единственно. Д.-ва: В силу теор. о неявной ф.-ции из ур.-ния 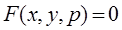 (5) можно локально выразить переменную p, т. е.
(5) можно локально выразить переменную p, т. е.  (6), где ϕ-непрер. диф. в окрестн. точки
(6), где ϕ-непрер. диф. в окрестн. точки  и
и  . Тем самым получаем задачу Коши
. Тем самым получаем задачу Коши  , Ǝ и единственность решения которой были установл. ранее.
, Ǝ и единственность решения которой были установл. ранее.
Интегральные кривые ур.-ния (1) удобнее изображать не на плоскости (x,y), а на 3ёх-мерном пространстве (x,y,p).  (1),
(1), 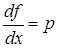 ,
,  .
.
 Множ. точек на поверхности, в котор.
Множ. точек на поверхности, в котор.  (3) нарушается, задаётся сист. ур.-ний
(3) нарушается, задаётся сист. ур.-ний  (7). Из системы (7) можно исключить параметр p и получить аналитич. условие:
(7). Из системы (7) можно исключить параметр p и получить аналитич. условие:  (8).
(8).
Вопрос 16. Дискриминантная кривая. Огибающая. Уравнения Лагранжа и Клеро.
Дf: Кривая, определённая уравнением  наз. дискриминантной. Её ветви могут быть решениями ур.-ния
наз. дискриминантной. Её ветви могут быть решениями ур.-ния  , соотв. достаточные условия сложны => на практике будем это проверять непосредственно подстановкой.
, соотв. достаточные условия сложны => на практике будем это проверять непосредственно подстановкой.
Рассм. 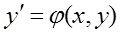 ,
,  ,
,  - неособ.точка, если Ǝ её окрестность U такая, что через любую точку этой окрестности проход. интегр. кривая и при том, только одна. В противном случае точка
- неособ.точка, если Ǝ её окрестность U такая, что через любую точку этой окрестности проход. интегр. кривая и при том, только одна. В противном случае точка  -особая точка. Дf: Решение, все точки котор. особые, наз. особым решением. Дf: Для ур.-ния
-особая точка. Дf: Решение, все точки котор. особые, наз. особым решением. Дf: Для ур.-ния  все точки решения y=0 явл. особыми. Аналогично
все точки решения y=0 явл. особыми. Аналогично  наз. неособой для ур.-ния
наз. неособой для ур.-ния  (1), если Ǝ её окрестн. U на поверхности S, через кажд. точку которой проходит интегр. кривая и при том, только одна. В противном случае эта точка-особая.
(1), если Ǝ её окрестн. U на поверхности S, через кажд. точку которой проходит интегр. кривая и при том, только одна. В противном случае эта точка-особая.
Пусть есть семейство кривых, определён. ур.-ем f(x,y,C)=0 (9),где С-некотор. параметр, f-действит. и непрер. диф. в некотор. области DᴄR3 и при том, выполн. условие  . дальнейш. рассуждения носят локальн. характер в малой окр. V точки (x0,y0,C0 ), где f(x0,y0,C0 )=0. Дf: Кривая γ наз. огибающей семейства кривых (9), если в кажд. своей точке она касается одной из кривых семейства и, если в разн. точках- касается разных кривых. Теорема: Огибающая γ семейства (9)- решений есть решение. Очевидно, что это семейство особое. Д.-ва: Пусть для определ.-ти семейства (9)-это решение ур.-ния
. дальнейш. рассуждения носят локальн. характер в малой окр. V точки (x0,y0,C0 ), где f(x0,y0,C0 )=0. Дf: Кривая γ наз. огибающей семейства кривых (9), если в кажд. своей точке она касается одной из кривых семейства и, если в разн. точках- касается разных кривых. Теорема: Огибающая γ семейства (9)- решений есть решение. Очевидно, что это семейство особое. Д.-ва: Пусть для определ.-ти семейства (9)-это решение ур.-ния  и
и  . Пусть далее кривая
. Пусть далее кривая 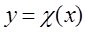 -интегр.-ая кривая, проход. через т.
-интегр.-ая кривая, проход. через т.  и
и  -ур.-ние кривой γ в окр. т.
-ур.-ние кривой γ в окр. т.  . Тогда
. Тогда  (10). Кривая
(10). Кривая  удовлетвор. условию (10). Подобному же условию будет удовлетвор. крив. γ, т. к.
удовлетвор. условию (10). Подобному же условию будет удовлетвор. крив. γ, т. к.  . =>, что эти 2е кривые касаются и => для кривой
. =>, что эти 2е кривые касаются и => для кривой 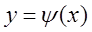 также выполн. условие (10),что означает, что она явл. решением ур.-ния
также выполн. условие (10),что означает, что она явл. решением ур.-ния  .(Ч. т. д.) Теорема: Пусть выполн. f=0 (9) и оператор
.(Ч. т. д.) Теорема: Пусть выполн. f=0 (9) и оператор  в окр. т.
в окр. т.  . Тогда в некотор. окр. U Ǝ т.
. Тогда в некотор. окр. U Ǝ т.  ,лежащие на огибающей семейства кривых (9), которая определ. из системы
,лежащие на огибающей семейства кривых (9), которая определ. из системы  . Д.-ва: (от противного) Пусть
. Д.-ва: (от противного) Пусть  и пусть для опред.-ти
и пусть для опред.-ти  в т.
в т.  . Покажем, что т.
. Покажем, что т.  не лежит на огибающей; тем самым теор. будет док.-на. Из ур.-ния (9) согласно теор. о неявн. ф.-ции выразим
не лежит на огибающей; тем самым теор. будет док.-на. Из ур.-ния (9) согласно теор. о неявн. ф.-ции выразим 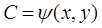 ,
,  непрер. диф. ф.-ция в достаточно малой в обл. V в т.
непрер. диф. ф.-ция в достаточно малой в обл. V в т. 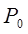 . Кроме того
. Кроме того  в т. Р0,т. к. из
в т. Р0,т. к. из 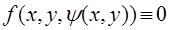 =>
=> 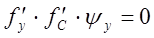 =>
=> 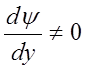 . Сделаем след. замену перемен.:
. Сделаем след. замену перемен.: 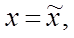
 (12).
(12).  =
=  =
= 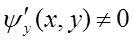 . При такой замене (12) огибающая переходит в вогибающую. В новых перемен. семейство (9) примет вид:
. При такой замене (12) огибающая переходит в вогибающую. В новых перемен. семейство (9) примет вид:  -семейство параллельных прямых, котор. не имеет огибающей.(Ч. Т. Д.). Вывод: чтобы найти ур.-ние огибающей нужно исключить С из системы (11), что даст некотор. ур.-ние g(x,y) =0, но определен. этим ур.-нием кривой может и не быть огибающ., т.к. теор. 3 даёт лишь достаточн. условие.
-семейство параллельных прямых, котор. не имеет огибающей.(Ч. Т. Д.). Вывод: чтобы найти ур.-ние огибающей нужно исключить С из системы (11), что даст некотор. ур.-ние g(x,y) =0, но определен. этим ур.-нием кривой может и не быть огибающ., т.к. теор. 3 даёт лишь достаточн. условие.
Уравнение Клеро.  (1)-ур.ние Клеро,
(1)-ур.ние Клеро, 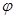 -непрер. диф. ф.-ция,
-непрер. диф. ф.-ция,  (2),
(2),  (3), найдём диф.-ал у и подставим в (3):
(3), найдём диф.-ал у и подставим в (3):  (4),
(4), 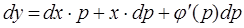 (5),
(5), 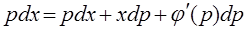 ,
,  . Подставим (6) в
. Подставим (6) в
(4):  -общ. решение ур.-ния Клеро. Подставим (7) в (4):
-общ. решение ур.-ния Клеро. Подставим (7) в (4): 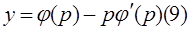 . Решение, определяющее сист.
. Решение, определяющее сист.  -особое решение ур.-ния Клеро (геометрически представляется огибающей).
-особое решение ур.-ния Клеро (геометрически представляется огибающей).
Уравнение Лагранжа:  -ур.-ние Лагранжа.
-ур.-ние Лагранжа.  ,
,  ,
,  ,
,  ,
,  ,
, 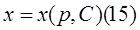 . Подставим (15) в (11), получаем параметрич. представл. общего решения ур.-ния Лагранжа.
. Подставим (15) в (11), получаем параметрич. представл. общего решения ур.-ния Лагранжа.
Вопрос 17. Классы уравнений п-го порядка, разрешаемые в квадратурах.
1a.  , f(x)-непрер. ф.-ция.
, f(x)-непрер. ф.-ция. 
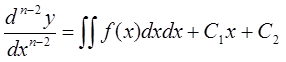 ,…,
,…, 
Ci-произвольные постоянные.
1b. 

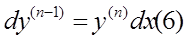
Найдём ф.-ции, соотв.-щие множителям:
 ,
,  ,
,
 ,…,
,…,

(4) и (9) доставл. в общее решение ур.-ния (3).
2а. 

Тогда ур. (10) превращается в ур. 1ого порядка:  -неполн.
-неполн.

 (14)
(14)
(14) подставим в (11):  -ур.-ние вида (1). Кажд. (n-1)-квадратуру находим, квадр.-уя:
-ур.-ние вида (1). Кажд. (n-1)-квадратуру находим, квадр.-уя: 
2b. 
 . Дано ур.-ние (17),котор. нельзя представить в виде (10).
. Дано ур.-ние (17),котор. нельзя представить в виде (10).
 . Воспользуемся соотношением (6):
. Воспользуемся соотношением (6):  . Подставим (18) в (16):
. Подставим (18) в (16): 




 . В (22) подстав. (19) интегр.: ……
. В (22) подстав. (19) интегр.: ……  рассм. сист.
рассм. сист.  , получим представл. общего решения в параметрич. форме.
, получим представл. общего решения в параметрич. форме.
3а. 



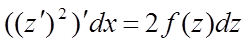
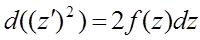



 . (25) подст. в (29):
. (25) подст. в (29):  -есть ур. (1). Взяв (n-2) квадратуры, получим общ. решение:
-есть ур. (1). Взяв (n-2) квадратуры, получим общ. решение:
3b. 

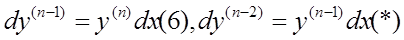 . Разделим (6) на (*) и умножим в пропорции крайние и средние:
. Разделим (6) на (*) и умножим в пропорции крайние и средние:
 . Подставим из (33) соотв. знач. в правую часть:
. Подставим из (33) соотв. знач. в правую часть: 
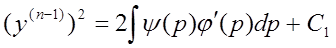



Вопрос 18. Теорема сущ-ния и единственности для системы лин.ур-я и для лин.ур-я n-ого порядка.
Теорема(Т.Пикара для норм.сист)пусть дано норм. сист. вида(1)  …
… 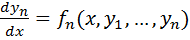 и поставим нач.условие
и поставим нач.условие  при
при  . Предположим,что ф-ии стоящие в правых частях сисит.(1) определ. В некотор. Ограничен. Замкнутой обл.R:
. Предположим,что ф-ии стоящие в правых частях сисит.(1) определ. В некотор. Ограничен. Замкнутой обл.R:  ,
, 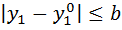 ,…,
,…,  , где a,b заданные положительные числа, а точка (
, где a,b заданные положительные числа, а точка ( )находится внутри (a,b).Пусть ф-ии стоящие в правых частях сист.(1) удовлетв.усл: 1.
)находится внутри (a,b).Пусть ф-ии стоящие в правых частях сист.(1) удовлетв.усл: 1.  ,k=1,n непрер.по всем своим аргумент.,а значит и ограничено
,k=1,n непрер.по всем своим аргумент.,а значит и ограничено  ,k=1,n, где
,k=1,n, где  -любые точки обл-ти R.2.ф-ии
-любые точки обл-ти R.2.ф-ии  имеют огран.частные производные по аргум.
имеют огран.частные производные по аргум.  т.е.
т.е.  при сделанном предположении сист.(1)имеет единствен. реш-е
при сделанном предположении сист.(1)имеет единствен. реш-е  ,
, 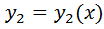 ..
..  удовлетв. Услов.
удовлетв. Услов.  ,
, 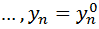 это решение определ. И непре-диф-ма в интервале
это решение определ. И непре-диф-ма в интервале  где
где  из теоремы следует,что если правые части сист.(1) явл. Многочленами от своих агрумен., то какие бы нач.усл.не взять
из теоремы следует,что если правые части сист.(1) явл. Многочленами от своих агрумен., то какие бы нач.усл.не взять  решен. этой сист. с данными нач.усл.
решен. этой сист. с данными нач.усл.
Общее решение.
Известно,что сист. реш.(1)зависит от n-произв.постоян.  т.е. такеи решен. имеют вид (3)
т.е. такеи решен. имеют вид (3)  ,
,  ….
….  такие решения обычно наз. общим решением сист.(1).Геометр.такое семейство решений представл. Собой мн-во интегр. Кривых в (n+1)-мерном простр-ве.Причем кажд.из ур.этого мн-ва зависит от n-параметров
такие решения обычно наз. общим решением сист.(1).Геометр.такое семейство решений представл. Собой мн-во интегр. Кривых в (n+1)-мерном простр-ве.Причем кажд.из ур.этого мн-ва зависит от n-параметров 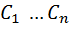 ,при этом из (3) видно,что кр-е этого семейства разреш. Относит.ф-ий
,при этом из (3) видно,что кр-е этого семейства разреш. Относит.ф-ий  …
… 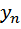 .
.
Опр. Совокупность ф-ий(3)определ. В некотор. Обл.изменень перем.  имеющие непрерывн. Частные производн. По xназ.общим решен. Сист.(1)в обл.R.простр.(
имеющие непрерывн. Частные производн. По xназ.общим решен. Сист.(1)в обл.R.простр.( ) в каждой точке,котор. Имеет место теорема
) в каждой точке,котор. Имеет место теорема  реш.задачи Коши. Если сист.(3) разрешима относительно производ. постоян.
реш.задачи Коши. Если сист.(3) разрешима относительно производ. постоян.  в обл.R так что при любом значении(
в обл.R так что при любом значении( ) принадлежащ. Этой обл.системой(3).определим значения
) принадлежащ. Этой обл.системой(3).определим значения  т.е.
т.е.  …
… 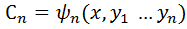 (4)-совокупность n-ф-ий (3)явл.решен.сист(1)при всех значен.производн.постоян.
(4)-совокупность n-ф-ий (3)явл.решен.сист(1)при всех значен.производн.постоян.  доставляемой ф-лой (4),когда т.(
доставляемой ф-лой (4),когда т.( ) пробегает всю обл.R.Формула общего реш-я(3) дает возможность за счет выбора значен.произв.постоян.решен.
) пробегает всю обл.R.Формула общего реш-я(3) дает возможность за счет выбора значен.произв.постоян.решен.  задачу Коши в обл.R,т.е.найти решение сист.(1) определяемое нач.данными(
задачу Коши в обл.R,т.е.найти решение сист.(1) определяемое нач.данными( )и при этом т. С такими координатами явл.
)и при этом т. С такими координатами явл.  т. Из обл.R.ЗАМЕЧАНИЕ:иногда в ф-ле общ.реш.(3) рольпроизв.постоян.
т. Из обл.R.ЗАМЕЧАНИЕ:иногда в ф-ле общ.реш.(3) рольпроизв.постоян.  играют начальные значения ф-ии
играют начальные значения ф-ии  при котор.фиксир.значении
при котор.фиксир.значении  аргум.x,ф-ла(3)примет вид:
аргум.x,ф-ла(3)примет вид:  …
… 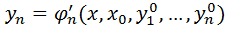 …такая форма записи решения наз.общим решением в форме Коши.
…такая форма записи решения наз.общим решением в форме Коши.
Частные решения.
Если решения сист.(1) сост.только из точек единственности решения задачи Коши для этой системы,т.е. когда  приним. Конкретное числовое значение,то такое решение наз.частным решением данной системы.Решение задачи Коши при помощи ф-лы общего решения сист.(1)явл.частным решением этой системы.
приним. Конкретное числовое значение,то такое решение наз.частным решением данной системы.Решение задачи Коши при помощи ф-лы общего решения сист.(1)явл.частным решением этой системы.
Особое решение.
Решение сист.(1)каждой т.которого нарушается единственность решения задачи Коши наз.особым решением. Если мы имеем частное реш.сист.(1),то через каждую точку обл.R проходит!-ая интегральная кривая A особое решение этой сист.характеризуется тем,что в нахождении т. Нарушается!-ть решения задачи Коши.т.е. через каждую точку этой обл.проходит не менее, чем две интегральные кривые.
Линейные системы д.у.
Лин.сист.д.у.наз.такие системы в которых производные от искомых ф-ий и сами искомые ф-ии содержаться только в 1-ой степени.т.е.она имеет вид:  …
…  такая система наз.однородной системой лин-ых ур-ий,если система имеет вид:
такая система наз.однородной системой лин-ых ур-ий,если система имеет вид: