плавной кривой, получим развертку секции. Развертки остальных одиннадцати секций будут
28. 28.Тени геометрических тел. Тень конуса прямого и обратного.
Тень геометрических тел
При построении теней от геометрических тел строят тени собственную и падающую (страница 4, 5).
Собственная тень формируется световыми лучами, касательными к поверхности.
Каждой точке собственной тени соответствует точка тени падающей. Если основание геометрического тела
располагается на плоскости проекций, построение тени упрощается. Блик – самая освещенная часть
поверхности предмета.

При построении тени конуса следует поступить иначе - сначала построить падающую тень, с помощью которой определяют затем контур собственной тени. Начинают с построения падающей тени вершины на плоскость основания конуса. Такой тенью является мнимая тень Sн. Касательные, проведенные из этой точки к основанию конуса, определяют теневые образующие конуса, которые и являются контуром собственной тени. Точки касания графически точно определяются с помощью окружности, построенной на проекции падающей тени S - Sн высоты конуса. Контур собственной тени конуса - линия касания боковой пов-ти конуса лучевыми плоскостями, паралл световым лучам, а контур падающей тени - гориз следы лучевых плоскостей.
| 2. Прямой общего положения называется прямая, не параллельная ни одной из плоскостей проекций. (рис.6) Рассмотрим схему построения ортогонального чертежа прямой линии. Так как две точки однозначно определяют положение прямой в пространстве, то нам достаточно задать на комплексном чертеже проекции двух точек, принадлежащих прямой и попарно соединить их первые, вторые и третьи проекции. Например, возьмём прямую m общего положения, заданную двумя точками А и В. Построим ортогональные проекции отрезка АВ на плоскости П1, П2, П3. Соединив ортогональные проекции точек А и В на каждой плоскости, мы получим ортогональную проекцию отрезка АВ на все три проецирующие плоскости. Определение длины отрезка прямой линиии углов наклона прямой к плоскостям проекций.Длину отрезка АВ можно определить из прямоугольного треугольника.(8,а,б) Гипотенуза Ао b прям.тр-ка и есть длина отрезка. Угол альфа в этом тр-ке опр=т угол наклона прямой к пл-ти Н.
Однако все построения можно объяснить, как вращение треугольника АВС вокруг стороны AС до тех пор, пока он не станет параллелен плоскости П 1, в этом случае треугольник проецируется на плоскость проекций без искажения.
Прямые частного положения (прямые,паралл.или перпенд.пл-тям проекций)
Частный случай расположения прямой:
1. прямые ║ плоскости проекции наз-ся линиями уровня; горизонталь -прямая, ║ гориз. пл-ти проекции.
2. фронталь – прямая, ║ фронтал. пл-ти проекции.
3.прямая, ║профил.пл-ти проекции – профильная.
Прямые перпенд. пл-тям:
1. прямая, перпенд. гориз. пл-ти проекции- гориз. проецирующая.
2. фронтально проец. прямая, ┴ фронт. пл-ти проекции.
  6. Взаимное положение плоскостей.Две пл-ти в пространстве могут быть либо параллельными, либо пересекающимися. Взаимно перпендикулярные пл-ти представляют собой частный случай пересекающихся пл-тей. Построение взаимно параллельных пл-тей.две пл-ти параллельны, если двум пересекающимся прямым, лежащим в одной пл-ти, соответствуют две параллельные пересекающиеся прямые другой пл-ти. Если же пл-ти заданы следами, то о взаимной параллельности их в пространстве можно судить по параллельности их одноименных следов.Построение параллельных пл-тей на чертеже удобно выполнять с помощью главных линий плоскости - горизонталей и фронталей. Прямая линия пересечения двух пл-тей определяется двумя точками, каждая из которых принадлежит обеим пл-тям. Или одной точкой, принадлежащей двум пл-тям, и известным направлением линии. В обоих случаях задача заключается в нахождении точки, общей для двух пл-тей. Общий прием построения линии пересечения двух пл-тей заключается в следующем: вводят вспомог. пл-ть, строят линии пересечения вспомогательной пл-ти с двумя заданными и в пересечении построенных линий находят общую точку двух пл-тей. Для нахождения второй общей точки построение повторяют с помощью еще одной вспомогательной пл-ти. Однако о параллельности профильно проецирующих пл-тей в пр-ве можно судить, лишь построив их профильные следы. Пересечение двух пл-тей. Две пл-ти пересекаются по прямой линии, общей для обеих пл-тей. Положение прямой линии опр-ся положением двух принадлежащих ей точек. Следовательно, для построения линии пересечения двух пл-тей достаточно определить две точки, общие для обеих заданных пл-тей. Если пл-ти заданы следами, то наиболее рационально отметить точки, являющиеся точками пересечения их одноименных следов (точки M и N прямой MN - линии пересечения пл-тей P и Q). Сущность этого метода состоит в том, что обе заданные пл-ти пересекаются третьей (обычно пл-тью частного положения - горизонтальной или фронтальной), затем строятся линии пересечения первой заданной пл-ти с третьей, второй заданной с третьей. Там, где эти линии пересекаются, отмечается точка, общая для заданных пл-тей. Вторая общая точка находится при помощи еще одной вспомогательной плоскости
Пересекающиеся плоскости. Построение линии пересечения пл-тей — одна из основных задач нач. геометрии. Она относится к так называемым позиционным задачам.
Позиционными наз-т задачи на определение общих эл-тов различных сопрягаемых геом-ких форм
Две пл-ти пересекаются по прямой линии. Поэтому для построения линии пересечения пл-тей необходимо опр-ть две точки этой прямой.
Рассмотрим частный случай пересечения пл-тей, когда одна из них — проецирующая.
На рис. 23, а приведены пл-ть общего положения Р и горизонтально проецирующая плоскость S. Двумя общими точками, принадлежащими обеим плоскостям, являются точки пересечения М и N одноименных следов этих плоскостей, которые и определяют линию пересечения.
Однако линия пересечения плоскостей может быть определена и другим образом. Если одна из пересекающихся плоскостей проецирующая, то одна из проекций линии пересечения совпадает с ее проецирующим следом. Горизонтальная проекция пт линии пересечения заданных плоскостей лежит на горизонтальном следе SH горизонтально проецирующей плоскости S. Фронтальная проекция линии пересечения определяется линиями связи.
На рис. 23, б показаны плоскость общего положения, заданная треугольником ABC, и фронтально проецирующая плоскость S. На фронтальной проекции в пересечении проецирующего следа плоскости Sv со сторонами треугольника получим две общие точки I' и 2' и фронтальную проекцию линии пересечения плоскостей. Горизонтальная проекция определяется с помощью про-ведения линии связи.
Рассмотрим общий случай пересечения, когда обе плоскости — общего положения. На рис. 24 приведены две плоскости, заданные следами. Как и в предыдущем примере, общими точками плоскостей являются точки пересечения М и N одноименных следов. Соединяя одноименные проекции этих точек прямой линией, получим проекции линии пересечения плоскостей.
Если точки пересечения одноименных следов находятся вне поля чертежа, а также в тех случаях, когда плоскости заданы не следами, а другими геометрическими элементами, то для оп-ределения линии пересечения плоскостей следует использовать вспомогательные плоскости уровня — горизонтальные или фронтальные.
На рис. 25 показаны две плоскости общего положения, заданные треугольником и двумя параллельными прямыми. Для определения двух общих точек линии пересечения плоскостей прово-дим две вспомогательные (горизонтальные) плоскости уровня S и Т. Вспомогательная плоскость S пересекает заданные плоскости по двум горизонталям й„ которые в своем пересечении определяют точку /, общую для плоскостей Р и Q, так как они одновременно принадлежат вспомогательной секущей плоскости S. Вторая вспомогательная плоскость Т также пересекает каждую из заданных плоскостей по горизонталям hp которые параллельны первым двум
горизонталям. В пересечении горизонталей получим вторую общую точку II заданных плоскостей. Соединяя на эпюре одноименные проекции этих точек, получим проекции линии пересечения плоскостей.
Необходимо отметить, что при построении линии пересечения плоскостей, заданных следами в предыдущем примере (см. рис. 24), роль вспомогательных секущих плоскостей выполняют плоскости проекций Я и V.
6. Взаимное положение плоскостей.Две пл-ти в пространстве могут быть либо параллельными, либо пересекающимися. Взаимно перпендикулярные пл-ти представляют собой частный случай пересекающихся пл-тей. Построение взаимно параллельных пл-тей.две пл-ти параллельны, если двум пересекающимся прямым, лежащим в одной пл-ти, соответствуют две параллельные пересекающиеся прямые другой пл-ти. Если же пл-ти заданы следами, то о взаимной параллельности их в пространстве можно судить по параллельности их одноименных следов.Построение параллельных пл-тей на чертеже удобно выполнять с помощью главных линий плоскости - горизонталей и фронталей. Прямая линия пересечения двух пл-тей определяется двумя точками, каждая из которых принадлежит обеим пл-тям. Или одной точкой, принадлежащей двум пл-тям, и известным направлением линии. В обоих случаях задача заключается в нахождении точки, общей для двух пл-тей. Общий прием построения линии пересечения двух пл-тей заключается в следующем: вводят вспомог. пл-ть, строят линии пересечения вспомогательной пл-ти с двумя заданными и в пересечении построенных линий находят общую точку двух пл-тей. Для нахождения второй общей точки построение повторяют с помощью еще одной вспомогательной пл-ти. Однако о параллельности профильно проецирующих пл-тей в пр-ве можно судить, лишь построив их профильные следы. Пересечение двух пл-тей. Две пл-ти пересекаются по прямой линии, общей для обеих пл-тей. Положение прямой линии опр-ся положением двух принадлежащих ей точек. Следовательно, для построения линии пересечения двух пл-тей достаточно определить две точки, общие для обеих заданных пл-тей. Если пл-ти заданы следами, то наиболее рационально отметить точки, являющиеся точками пересечения их одноименных следов (точки M и N прямой MN - линии пересечения пл-тей P и Q). Сущность этого метода состоит в том, что обе заданные пл-ти пересекаются третьей (обычно пл-тью частного положения - горизонтальной или фронтальной), затем строятся линии пересечения первой заданной пл-ти с третьей, второй заданной с третьей. Там, где эти линии пересекаются, отмечается точка, общая для заданных пл-тей. Вторая общая точка находится при помощи еще одной вспомогательной плоскости
Пересекающиеся плоскости. Построение линии пересечения пл-тей — одна из основных задач нач. геометрии. Она относится к так называемым позиционным задачам.
Позиционными наз-т задачи на определение общих эл-тов различных сопрягаемых геом-ких форм
Две пл-ти пересекаются по прямой линии. Поэтому для построения линии пересечения пл-тей необходимо опр-ть две точки этой прямой.
Рассмотрим частный случай пересечения пл-тей, когда одна из них — проецирующая.
На рис. 23, а приведены пл-ть общего положения Р и горизонтально проецирующая плоскость S. Двумя общими точками, принадлежащими обеим плоскостям, являются точки пересечения М и N одноименных следов этих плоскостей, которые и определяют линию пересечения.
Однако линия пересечения плоскостей может быть определена и другим образом. Если одна из пересекающихся плоскостей проецирующая, то одна из проекций линии пересечения совпадает с ее проецирующим следом. Горизонтальная проекция пт линии пересечения заданных плоскостей лежит на горизонтальном следе SH горизонтально проецирующей плоскости S. Фронтальная проекция линии пересечения определяется линиями связи.
На рис. 23, б показаны плоскость общего положения, заданная треугольником ABC, и фронтально проецирующая плоскость S. На фронтальной проекции в пересечении проецирующего следа плоскости Sv со сторонами треугольника получим две общие точки I' и 2' и фронтальную проекцию линии пересечения плоскостей. Горизонтальная проекция определяется с помощью про-ведения линии связи.
Рассмотрим общий случай пересечения, когда обе плоскости — общего положения. На рис. 24 приведены две плоскости, заданные следами. Как и в предыдущем примере, общими точками плоскостей являются точки пересечения М и N одноименных следов. Соединяя одноименные проекции этих точек прямой линией, получим проекции линии пересечения плоскостей.
Если точки пересечения одноименных следов находятся вне поля чертежа, а также в тех случаях, когда плоскости заданы не следами, а другими геометрическими элементами, то для оп-ределения линии пересечения плоскостей следует использовать вспомогательные плоскости уровня — горизонтальные или фронтальные.
На рис. 25 показаны две плоскости общего положения, заданные треугольником и двумя параллельными прямыми. Для определения двух общих точек линии пересечения плоскостей прово-дим две вспомогательные (горизонтальные) плоскости уровня S и Т. Вспомогательная плоскость S пересекает заданные плоскости по двум горизонталям й„ которые в своем пересечении определяют точку /, общую для плоскостей Р и Q, так как они одновременно принадлежат вспомогательной секущей плоскости S. Вторая вспомогательная плоскость Т также пересекает каждую из заданных плоскостей по горизонталям hp которые параллельны первым двум
горизонталям. В пересечении горизонталей получим вторую общую точку II заданных плоскостей. Соединяя на эпюре одноименные проекции этих точек, получим проекции линии пересечения плоскостей.
Необходимо отметить, что при построении линии пересечения плоскостей, заданных следами в предыдущем примере (см. рис. 24), роль вспомогательных секущих плоскостей выполняют плоскости проекций Я и V.
  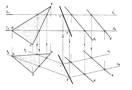 9. Способы преобразования проекций:
Способы преобразования предназначены гл.образом для решения метрических задач, связанных с определением дествит-х размеров и формы изобр-ых на эпюре геометр. объектов.
Основные способы преобразования проекций:
а) способ замены пл-тей проекции
б) способ вращения
в) способ косоугольного вспомогательного проецирования.
Новые проекции точек и осей проекций обозначают теми же буквами, но с цифровым индексом внизу, который опр-т последова-ть преобразований.
Способ замены пл-тей проекций. Сущность способа замены пл-тей проекций заключается в том, что при неизменном положении объекта в пространстве производится замена данной системы плоскостей проекцией новой системой взаимно перпендикулярных пл-тей проекций (рис. 33, а). При переходе к новой системе одну из плоскостей проекций заменяют новой пл-тью таким образом, чтобы данный геометрический элемент (прямая, пл-ть) занял частное положение и проецировался без искажения.
При решении ряда метрических задач требуется преобразовать прямую общего положения в прямую уровня, а затем — в проецирующую, выполнив при этом последовательно два преобразования.
Рассмотрим ход решения этой задачи.
1-е преобразование (рис. 33, б). Для того чтобы прямая АВ спроецировалась линией уровня, следует ввести новую плоскость проекций и расположить ее параллельно данной прямой. При этом новая ось jc, будет параллельна одной из проекций прямой. На рис. 33, а, б ось проведена параллельно горизонтальной проекции ab, а новая плоскость проекций Vl расположена параллельно прямой АВ, которая проецируется на эту плоскость в истинную величину (новая фронтальная проекция прямой — а\Ь\). Новая ось х, и плоскость проекции V, могут быть расположены на любом расстоянии от прямой, они могут совпадать с прямой и ее проекцией.
При замене плоскостей проекций расстояние от новой проекции точки до новой оси равно расстоянию от заменяемой проекции точки до старой оси проекций. Иными словами, высоты (аппликаты) концов отрезка в новой системе плоскостей проекций останутся прежними. В результате этой замены определены действительная величина отрезка прямой и угол наклона а к пл-ти Н. При переходе к эпюру плоскость совмещается с плоскостью Н.
2-е преобразование (рис. 33, в). Для того чтобы прямая АВ оказалась проецирующей, т. е. изобразилась точкой, необходимо произвести вторую замену плоскости проекций и расположить новую плоскость Н, перпендикулярно прямой. Новая ось х2 выбрана на эпюре перпендикулярной новой фронтальной проекции прямой а'ХЪ\. На новой пл-ти проекций Ну прямая изобразится точкой, так как координаты концов отрезка в системе H1V1 одинаковы.
Т.о., прямая А В в системе HjVl стала проецирующей относительно пл-ти Н1.
Рассмотрим еще одну задачу — требуется определить истинную величину плоской фигуры — треугольника ABC, занимающего в пространстве общее положение. Для решения этой задачи необходимо преобразовать эпюр так, чтобы плоскость общего положения стала параллельной одной из плоскостей проекций новой системы. В ортогонально-проекционной системе решить эту задачу одной заменой плоскости проекций нельзя. Как и в предыдущей задаче, необходимо выполнить два преобразования, но в иной последовальности: сначала следует преобразовать плоскость общего положения в проецирующую, а затем — в плоскость уровня.
На рис. 34, а сначала заменена фронтальная плоскость проекций новой плоскостью F„ перпендикулярной плоскости треугольника. Это условие выполнено с помощью вспомогательной прямой — линии уровня, например, горизонтали AN (рис. 34, б). Новая ось хх проведена на эпюре перпендикулярно горизонтальной проекции горизонтали. На новой плоскости проекций У, горизонталь спроецировалась в точку, а плоскость треугольника — в линию.
Угол а определяет угол наклона треугольника к горизонтальной плоскости Н.
На втором этапе решения проведена вторая замена — новая плоскость проекций Я, установлена параллельно треугольнику. Новая ось х2 проведена параллельно новой фронтальной проекции треугольника — прямой b\a\d Построенная проекция определяет истинную величину и форму треугольника.
Если плоскость задана следами, а не плоской фигурой, ее следует преобразовать в проецирующую. Для этого новую плоскость проекций и новую ось проекций следует расположить перпен-дикулярно, например, к горизонтальному следу заданной плоскости (рис. 35),
при этом горизонтальный след спроецируется на новой плоскости в точку (Рх).
Для построения новой проекции фронтального следа Pv достаточно найти
проекцию любой точки заданной плоскости, например произвольной точки N, лежащей на следе. Прямая Р—п, является искомым проецирующим следом данной плоскости.
9. Способы преобразования проекций:
Способы преобразования предназначены гл.образом для решения метрических задач, связанных с определением дествит-х размеров и формы изобр-ых на эпюре геометр. объектов.
Основные способы преобразования проекций:
а) способ замены пл-тей проекции
б) способ вращения
в) способ косоугольного вспомогательного проецирования.
Новые проекции точек и осей проекций обозначают теми же буквами, но с цифровым индексом внизу, который опр-т последова-ть преобразований.
Способ замены пл-тей проекций. Сущность способа замены пл-тей проекций заключается в том, что при неизменном положении объекта в пространстве производится замена данной системы плоскостей проекцией новой системой взаимно перпендикулярных пл-тей проекций (рис. 33, а). При переходе к новой системе одну из плоскостей проекций заменяют новой пл-тью таким образом, чтобы данный геометрический элемент (прямая, пл-ть) занял частное положение и проецировался без искажения.
При решении ряда метрических задач требуется преобразовать прямую общего положения в прямую уровня, а затем — в проецирующую, выполнив при этом последовательно два преобразования.
Рассмотрим ход решения этой задачи.
1-е преобразование (рис. 33, б). Для того чтобы прямая АВ спроецировалась линией уровня, следует ввести новую плоскость проекций и расположить ее параллельно данной прямой. При этом новая ось jc, будет параллельна одной из проекций прямой. На рис. 33, а, б ось проведена параллельно горизонтальной проекции ab, а новая плоскость проекций Vl расположена параллельно прямой АВ, которая проецируется на эту плоскость в истинную величину (новая фронтальная проекция прямой — а\Ь\). Новая ось х, и плоскость проекции V, могут быть расположены на любом расстоянии от прямой, они могут совпадать с прямой и ее проекцией.
При замене плоскостей проекций расстояние от новой проекции точки до новой оси равно расстоянию от заменяемой проекции точки до старой оси проекций. Иными словами, высоты (аппликаты) концов отрезка в новой системе плоскостей проекций останутся прежними. В результате этой замены определены действительная величина отрезка прямой и угол наклона а к пл-ти Н. При переходе к эпюру плоскость совмещается с плоскостью Н.
2-е преобразование (рис. 33, в). Для того чтобы прямая АВ оказалась проецирующей, т. е. изобразилась точкой, необходимо произвести вторую замену плоскости проекций и расположить новую плоскость Н, перпендикулярно прямой. Новая ось х2 выбрана на эпюре перпендикулярной новой фронтальной проекции прямой а'ХЪ\. На новой пл-ти проекций Ну прямая изобразится точкой, так как координаты концов отрезка в системе H1V1 одинаковы.
Т.о., прямая А В в системе HjVl стала проецирующей относительно пл-ти Н1.
Рассмотрим еще одну задачу — требуется определить истинную величину плоской фигуры — треугольника ABC, занимающего в пространстве общее положение. Для решения этой задачи необходимо преобразовать эпюр так, чтобы плоскость общего положения стала параллельной одной из плоскостей проекций новой системы. В ортогонально-проекционной системе решить эту задачу одной заменой плоскости проекций нельзя. Как и в предыдущей задаче, необходимо выполнить два преобразования, но в иной последовальности: сначала следует преобразовать плоскость общего положения в проецирующую, а затем — в плоскость уровня.
На рис. 34, а сначала заменена фронтальная плоскость проекций новой плоскостью F„ перпендикулярной плоскости треугольника. Это условие выполнено с помощью вспомогательной прямой — линии уровня, например, горизонтали AN (рис. 34, б). Новая ось хх проведена на эпюре перпендикулярно горизонтальной проекции горизонтали. На новой плоскости проекций У, горизонталь спроецировалась в точку, а плоскость треугольника — в линию.
Угол а определяет угол наклона треугольника к горизонтальной плоскости Н.
На втором этапе решения проведена вторая замена — новая плоскость проекций Я, установлена параллельно треугольнику. Новая ось х2 проведена параллельно новой фронтальной проекции треугольника — прямой b\a\d Построенная проекция определяет истинную величину и форму треугольника.
Если плоскость задана следами, а не плоской фигурой, ее следует преобразовать в проецирующую. Для этого новую плоскость проекций и новую ось проекций следует расположить перпен-дикулярно, например, к горизонтальному следу заданной плоскости (рис. 35),
при этом горизонтальный след спроецируется на новой плоскости в точку (Рх).
Для построения новой проекции фронтального следа Pv достаточно найти
проекцию любой точки заданной плоскости, например произвольной точки N, лежащей на следе. Прямая Р—п, является искомым проецирующим следом данной плоскости.  
 13. Многогранники – замкнутые пространственные фигуры, ограниченные плоскими многоугольниками. Многогранник называется метрически правильным, если все его грани являются правильными многоугольниками. К ним относятся куб, тетраэдр, октаэдр, икосаэдр, додекаэдр.Тетраэдр(четырехгранник) - ограничен четырьмя равносторонними и равными треугольниками.Гексаэдр(четырехгранник, или куб) - ограничен шестью равными квадратами. Октаэдр(восьмигранник) - ограничен восемью равносторонними и равными треугольниками. Додекаэдр(двенадцатигранник) - ограничен двенадцатью равносторонними и равными пятиугольниками. Икосаэдр(двадцатигранник) - ограничен двадцатью равносторонними и равными треугольниками.Пирамида- это многогранник, одна грань которого многоугольник, а остальные грани - треугольники с общей вершиной. Пирамида называется правильной, если в основании лежит правильный многоугольник и высота пирамиды проходит через центр многоугольника. Пирамида называется усеченной, если вершина её отсекается плоскостью (рис.6.1.).Призма- многоугольник, две грани которого (основания призмы) представляют собой равные многоугольники с взаимно параллельными сторонами, а все другие грани параллелограммы. Призма называется прямой, если её ребра перпендикулярны плоскости основания. Если основанием призмы является прямоугольник, призму называют параллелепипедом (рис 6.2.). Тетраэдр - правильный четырехгранник (рис 6.4.). Он ограничен четырьмя равносторонними треугольниками (это правильная треугольная пирамида).
17. Пересечение многогранных поверхностей.??? Взаимное пересечение поверхностейЛинией пересечения двух поверхностей является множество точек, общих для данных поверхностей. Из этого множества выделяют характерные (опорные, или главные) точки, с которых следует начинать построение этой линии. Они позволяют увидеть, в каких границах можно изменять положение вспомогательных секущих поверхностей для определения остальных точек.К таким точкам относятся: экстремальные точки- верхняя и нижняя точки относительно той или иной плоскости проекций; точки, расположенные на очерковых образующих некоторых поверхностей точки границы зоны видимости и т.д.Следует имеет в виду, что линия пересечения двух поверхностей в проекциях всегда располагается в пределах контура наложения проекций двух пересекающихся поверхностей.
Иногда целесообразно воспользоваться преобразованием чертежа, чтобы представить пересекающиеся поверхности (или одну из них) в частном положении.Для определения этих точек часто пользуются вспомогательными секущими поверхностями. Поверхности-посредники пересекают данные поверхности по линиям, которые, в свою очередь, пересекаются в точках линии пересечения данных поверхностей.Секущие поверхности-посредники выбираются так, чтобы они, пересекаясь с данными поверхностями, давали простые для построения линии, например прямые и окружности.Из общей схемы построения линии пересечения поверхностей выделяют два основных метода - метод секущих плоскостей и метод секущих сфер.В общем случае решение задачи по построении линии пересечения двух поверхностей может быть сведено к рассмотренным ранее задачам по определению:
1. Точек пересечения линии с поверхностью;
2. Линии пересечения плоскости и поверхности;
3. Комбинации первой и второй задачи.
21.
21.Кривые поверхности. Классификация поверхностей.
Кривой поверхностью называется совокупность последовательных положений линии (образующей), движущейся в пространстве по некоторому закону.
Закон движения образующей определяется неподвижными направляющими элементами и положением образующей относительно этих элементов в любой момент движения. Таким образом, определителем кривой поверхности является:
1. Образующая (прямая или кривая линия);
2. Направляющие элементы (точки, прямые, кривые линии, плоскости);
3. Условия, определяющие положение образующей относительно направляющих элементов.
Например, коническая поверхность (рис. 10, а) образуется движением прямой линии l, которая в каждый момент движения пересекает кривую линию m и проходит через неподвижную точку S. Здесь l – образующая, m и S – направляющие. Условная запись определителя поверхности: q (l,m, S; l ∩ m; l ' S).
Построение проекций кривой поверхностисводится к построению проекций параметров определителя (рис. 10, б) или очерков проекций.
Построение точки, принадлежащей кривой поверхности: на заданной поверхности провести какую-либо по возможности простейшую линию (образующую, параллель…) и на ней задать точку. На рис. 10, в точка А принадлежит направляющей m, точка К принадлежит образующей SА.
Классификация поверхностей.
Из большего числа возможных способов образования поверхностей рассмотрим основные способы, выделив главные признаки их классификации.
1. По закону движения образующей-поверхности с поступательным движением образующей, с вращательным и винтовым движением образующей.
2. По виду образующей различают поверхности с прямолинейной образующей- линейчатые и поверхности с криволинейной образующей - нелинейчатые
3. По закону изменения формы образующей – с образующей постоянного или переменного вида.
4. По признаку развертывания поверхности на плоскость – развертываемые и неразвертываемые.
5. По способу задания поверхности – аналитическому или графическому.
6. По дифференциальным свойствам – гладкие или не гладкие поверхности и по признаку кривизны поверхности
Необходимо отметить, что одни и те же поверхности могут быть классифицированы по различным признакам.
25.Теоретические основы построения теней в ортогональных проекциях. Направление световых лучей (тень от точки)
Назначение теней.
Тени строят на фасадах зданий и сооружений, на планах застройки района или
квартала для придания чертежу наглядности и выразительности. Построение теней выполняется для выявления освещенности отдельных элементов проектируемого здания или сооружения.
По форме и размерам тени можно определить форму и размеры предмета, отбрасывающего тень.
Основная задача теории теней
Основная задача теории теней – определение контуров собственной и
падающей тени данного объекта. Собственная тень – неосвещенная часть поверхности предмета.
Падающая тень – тень, отбрасываемая предметом на плоскости проекций и другие предметы.
Каждой точке контура собственной тени соответствует определенная точка контура падающей тени.
Основные понятия
Освещение предмета может быть факельным, если источник света удален от предмета на незначительное расстояние. Освещение предмета может быть солнечным, если источник света удален в бесконечность. При таком освещении:
* источник света – Солнце - удален в бесконечность;
* световые лучи распространяются прямолинейно;
* световые лучи параллельны друг другу.
За направление световых лучей S принимают направление одной из диагоналей куба, грани которого параллельны плоскостям проекций. Ортогональные проекции луча S на плоскости проекций составляют с осями координат угол 45°.
тени от точки
Иногда возникает необходимость построить тень точки, которой в действительности нет. Такую тень
называют мнимой (смотри страницу 12,26, 28). А т – действительная (реальная) тень точки А
на фронтальную плоскость проекций А T м – мнимая (воображаемая) тень точки А на горизонтальную плоскость проекций. Построение А T м видно из чертежа.
13. Многогранники – замкнутые пространственные фигуры, ограниченные плоскими многоугольниками. Многогранник называется метрически правильным, если все его грани являются правильными многоугольниками. К ним относятся куб, тетраэдр, октаэдр, икосаэдр, додекаэдр.Тетраэдр(четырехгранник) - ограничен четырьмя равносторонними и равными треугольниками.Гексаэдр(четырехгранник, или куб) - ограничен шестью равными квадратами. Октаэдр(восьмигранник) - ограничен восемью равносторонними и равными треугольниками. Додекаэдр(двенадцатигранник) - ограничен двенадцатью равносторонними и равными пятиугольниками. Икосаэдр(двадцатигранник) - ограничен двадцатью равносторонними и равными треугольниками.Пирамида- это многогранник, одна грань которого многоугольник, а остальные грани - треугольники с общей вершиной. Пирамида называется правильной, если в основании лежит правильный многоугольник и высота пирамиды проходит через центр многоугольника. Пирамида называется усеченной, если вершина её отсекается плоскостью (рис.6.1.).Призма- многоугольник, две грани которого (основания призмы) представляют собой равные многоугольники с взаимно параллельными сторонами, а все другие грани параллелограммы. Призма называется прямой, если её ребра перпендикулярны плоскости основания. Если основанием призмы является прямоугольник, призму называют параллелепипедом (рис 6.2.). Тетраэдр - правильный четырехгранник (рис 6.4.). Он ограничен четырьмя равносторонними треугольниками (это правильная треугольная пирамида).
17. Пересечение многогранных поверхностей.??? Взаимное пересечение поверхностейЛинией пересечения двух поверхностей является множество точек, общих для данных поверхностей. Из этого множества выделяют характерные (опорные, или главные) точки, с которых следует начинать построение этой линии. Они позволяют увидеть, в каких границах можно изменять положение вспомогательных секущих поверхностей для определения остальных точек.К таким точкам относятся: экстремальные точки- верхняя и нижняя точки относительно той или иной плоскости проекций; точки, расположенные на очерковых образующих некоторых поверхностей точки границы зоны видимости и т.д.Следует имеет в виду, что линия пересечения двух поверхностей в проекциях всегда располагается в пределах контура наложения проекций двух пересекающихся поверхностей.
Иногда целесообразно воспользоваться преобразованием чертежа, чтобы представить пересекающиеся поверхности (или одну из них) в частном положении.Для определения этих точек часто пользуются вспомогательными секущими поверхностями. Поверхности-посредники пересекают данные поверхности по линиям, которые, в свою очередь, пересекаются в точках линии пересечения данных поверхностей.Секущие поверхности-посредники выбираются так, чтобы они, пересекаясь с данными поверхностями, давали простые для построения линии, например прямые и окружности.Из общей схемы построения линии пересечения поверхностей выделяют два основных метода - метод секущих плоскостей и метод секущих сфер.В общем случае решение задачи по построении линии пересечения двух поверхностей может быть сведено к рассмотренным ранее задачам по определению:
1. Точек пересечения линии с поверхностью;
2. Линии пересечения плоскости и поверхности;
3. Комбинации первой и второй задачи.
21.
21.Кривые поверхности. Классификация поверхностей.
Кривой поверхностью называется совокупность последовательных положений линии (образующей), движущейся в пространстве по некоторому закону.
Закон движения образующей определяется неподвижными направляющими элементами и положением образующей относительно этих элементов в любой момент движения. Таким образом, определителем кривой поверхности является:
1. Образующая (прямая или кривая линия);
2. Направляющие элементы (точки, прямые, кривые линии, плоскости);
3. Условия, определяющие положение образующей относительно направляющих элементов.
Например, коническая поверхность (рис. 10, а) образуется движением прямой линии l, которая в каждый момент движения пересекает кривую линию m и проходит через неподвижную точку S. Здесь l – образующая, m и S – направляющие. Условная запись определителя поверхности: q (l,m, S; l ∩ m; l ' S).
Построение проекций кривой поверхностисводится к построению проекций параметров определителя (рис. 10, б) или очерков проекций.
Построение точки, принадлежащей кривой поверхности: на заданной поверхности провести какую-либо по возможности простейшую линию (образующую, параллель…) и на ней задать точку. На рис. 10, в точка А принадлежит направляющей m, точка К принадлежит образующей SА.
Классификация поверхностей.
Из большего числа возможных способов образования поверхностей рассмотрим основные способы, выделив главные признаки их классификации.
1. По закону движения образующей-поверхности с поступательным движением образующей, с вращательным и винтовым движением образующей.
2. По виду образующей различают поверхности с прямолинейной образующей- линейчатые и поверхности с криволинейной образующей - нелинейчатые
3. По закону изменения формы образующей – с образующей постоянного или переменного вида.
4. По признаку развертывания поверхности на плоскость – развертываемые и неразвертываемые.
5. По способу задания поверхности – аналитическому или графическому.
6. По дифференциальным свойствам – гладкие или не гладкие поверхности и по признаку кривизны поверхности
Необходимо отметить, что одни и те же поверхности могут быть классифицированы по различным признакам.
25.Теоретические основы построения теней в ортогональных проекциях. Направление световых лучей (тень от точки)
Назначение теней.
Тени строят на фасадах зданий и сооружений, на планах застройки района или
квартала для придания чертежу наглядности и выразительности. Построение теней выполняется для выявления освещенности отдельных элементов проектируемого здания или сооружения.
По форме и размерам тени можно определить форму и размеры предмета, отбрасывающего тень.
Основная задача теории теней
Основная задача теории теней – определение контуров собственной и
падающей тени данного объекта. Собственная тень – неосвещенная часть поверхности предмета.
Падающая тень – тень, отбрасываемая предметом на плоскости проекций и другие предметы.
Каждой точке контура собственной тени соответствует определенная точка контура падающей тени.
Основные понятия
Освещение предмета может быть факельным, если источник света удален от предмета на незначительное расстояние. Освещение предмета может быть солнечным, если источник света удален в бесконечность. При таком освещении:
* источник света – Солнце - удален в бесконечность;
* световые лучи распространяются прямолинейно;
* световые лучи параллельны друг другу.
За направление световых лучей S принимают направление одной из диагоналей куба, грани которого параллельны плоскостям проекций. Ортогональные проекции луча S на плоскости проекций составляют с осями координат угол 45°.
тени от точки
Иногда возникает необходимость построить тень точки, которой в действительности нет. Такую тень
называют мнимой (смотри страницу 12,26, 28). А т – действительная (реальная) тень точки А
на фронтальную плоскость проекций А T м – мнимая (воображаемая) тень точки А на горизонтальную плоскость проекций. Построение А T м видно из чертежа.
 Тень точки
Падающая тень точки является точкой пересечения светового луча S, проходящего через нее, с
поверхностью или плоскостью, а которую падает тень. Тень точки упадет на ту плоскость проекций, которую световой луч встретит раньше, то есть к которой точка располагается ближе.Построение тени точки способом равнобедренного прямоугольного треугольника
Можно построить тень точки, не проводя световые лучи, а формируя прямоугольный равнобедренный треугольник по направлению светового луча, как показано на чертеже.
Тень точки
Падающая тень точки является точкой пересечения светового луча S, проходящего через нее, с
поверхностью или плоскостью, а которую падает тень. Тень точки упадет на ту плоскость проекций, которую световой луч встретит раньше, то есть к которой точка располагается ближе.Построение тени точки способом равнобедренного прямоугольного треугольника
Можно построить тень точки, не проводя световые лучи, а формируя прямоугольный равнобедренный треугольник по направлению светового луча, как показано на чертеже.
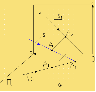
| 3. Следом прямой называется, точка пересечения прямой с плоскостью проекций.(рис. 9 ): М(т\т') — горизонтальный след прямой; N{n;n') — фронтальный след. На рис. 9, б дан эпюр прямой АВ, а также горизонтальный и фронтальный следы прямой.
Для определения на эпюре горизонтального следа прямой необходимо продолжить ее фронтальную проекцию до пересечения с осью Ох и в этой точке восставить перпендикуляр до пересечения с горизонтальной проекцией прямой. Фронтальная проекция фронтального следа и горизонтальная проекция горизонтального следа будут лежать в плоскостях проекций и совпадать с самим следом (на оси проекций). Следы прямой явл-ся точками, в которых прямая переходит из одной четверти в другую.
Прямая, расположенная параллельно плоскости проекций, следа на ней не имеет.
Взаимное положение прямых.Как известно, прямые в пространстве могут быть пересекающимися, параллельными (10) или скрещивающимися. (скрещивающимися прямыми называются прямые, которые не пересекаются и не параллельны между собой).Пересекающиеся прямые линии имеют общую собственную точку, параллельные - общую несобственную точку, скрещивающиеся прямые не имеют общих точек.Прямые линии могут пересекаться под прямым углом. Скрещивающиеся прямые тоже могут быть взаимно перпендикулярными.
1. Пересекающиеся прямые Пересекающимися прямыми называются такие прямые, которые имеют одну общую точку. проекция точки пересечения проекций прямых а и b есть точка пересечения этих прямых 2. Параллельные прямые прямые, пересекающиеся в несобственной точке (прямые, лежащие в одной плоскости и пересекающиеся в бесконечно удаленной точке).Из инвариантного свойства 6 следует, что проекции параллельных прямых а и b параллельны. 3. Скрещивающиеся прямые – это прямые, не лежащие в одной плоскости, это прямые не имеющие ни одной общей точки. точки пересечения проекций этих прямых не лежат на одном перпендикуляре к оси x 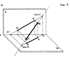    .
7. Взаимное положение прямой линии и плоскости.
Прямая может находиться в пл-ти, быть параллельной ей или пересекать пл-ть.
При пересечении прямой линии с пл-тью следует выделить частный случай, когда прямая перпенд. пл-ти.
Прямая перпендикулярная пл-ти, если её проекции перпендикулярны одноименным следам пл-ти или соответствующим проекциям горизонтали и фронтали.
(рис. 31). На рис. 31, а, б показана прямая АВ, перпендикулярная пл-ти Р, заданной следами. Проведем в пл-ти Р через точку В горизонталь. На основе правила проецирования прямого угла,угол, образованный перпендикуляром А В и горизонталью, будет проецироваться на пл-ти Н прямым (abn=90°). Аналогичный вывод можно сделать и в отношении фронтальной проекции перпендикуляра.
Для того чтобы построить прямую, перпендикулярную пл-ти, заданной треугольником BCD (рис. 31, в), не следует строить следы пл-ти. Необходимо сначала построить в пл-ти горизонталь и фронталь, а затем провести проекции перпендикуляра под прямым углом к одноименным проекциям горизонтали и фронтали.
Т.о., если прямая перпендикулярна двум пересекающимся прямым, принадлежащим пл-ти,
то она перпендикулярна и самой пл-ти.
Приведенное положение дает возможность решать ряд задач и, в частности, опустить или восставить перпендикуляр к пл-ти, решить обратную задачу — провести плоскость перпендикулярно прямой, определить расстояние от точки до пл-ти.
Пусть требуется определить расстояние от точки до пл-ти. Иными словами, необходимо определить длину перпендикуляра, опущенного из данной точки на пл-ть.Задача решается в три этапа, каждый из которых представляет собой одну из рассмотренных ранее задач: 1) определить направление проекций перпендикуляра к пл-ти; 2) построить точку пересечения прямой (перпендикуляра) с пл-тью; 3) определить длину перпендикуляра способом прямоугольного треугольника.
.
7. Взаимное положение прямой линии и плоскости.
Прямая может находиться в пл-ти, быть параллельной ей или пересекать пл-ть.
При пересечении прямой линии с пл-тью следует выделить частный случай, когда прямая перпенд. пл-ти.
Прямая перпендикулярная пл-ти, если её проекции перпендикулярны одноименным следам пл-ти или соответствующим проекциям горизонтали и фронтали.
(рис. 31). На рис. 31, а, б показана прямая АВ, перпендикулярная пл-ти Р, заданной следами. Проведем в пл-ти Р через точку В горизонталь. На основе правила проецирования прямого угла,угол, образованный перпендикуляром А В и горизонталью, будет проецироваться на пл-ти Н прямым (abn=90°). Аналогичный вывод можно сделать и в отношении фронтальной проекции перпендикуляра.
Для того чтобы построить прямую, перпендикулярную пл-ти, заданной треугольником BCD (рис. 31, в), не следует строить следы пл-ти. Необходимо сначала построить в пл-ти горизонталь и фронталь, а затем провести проекции перпендикуляра под прямым углом к одноименным проекциям горизонтали и фронтали.
Т.о., если прямая перпендикулярна двум пересекающимся прямым, принадлежащим пл-ти,
то она перпендикулярна и самой пл-ти.
Приведенное положение дает возможность решать ряд задач и, в частности, опустить или восставить перпендикуляр к пл-ти, решить обратную задачу — провести плоскость перпендикулярно прямой, определить расстояние от точки до пл-ти.
Пусть требуется определить расстояние от точки до пл-ти. Иными словами, необходимо определить длину перпендикуляра, опущенного из данной точки на пл-ть.Задача решается в три этапа, каждый из которых представляет собой одну из рассмотренных ранее задач: 1) определить направление проекций перпендикуляра к пл-ти; 2) построить точку пересечения прямой (перпендикуляра) с пл-тью; 3) определить длину перпендикуляра способом прямоугольного треугольника.
  10. Способы преобразования проекций:
Способы преобразования предназначены гл.образом для решения метрических задач, связанных с определением дествит-х размеров и формы изобр-ых на эпюре геометр. объектов.
Основные способы преобразования проекций:
а) способ замены пл-тей проекции
б) способ вращения
в) способ косоугольного вспомогательного проецирования.
Новые проекции точек и осей проекций обозначают теми же буквами, но с цифровым индексом внизу, который опр-т последова-ть преобразований.
Способ косоугольного вспомог.проецирования.
Способы решения задач применяют при решении как метрических, так и позиционных задач. Сущность этого способа закл-ся в применении не прямоугольного, а косоугольного проецирования. Направление проецирование выбирается т.о., чтобы получить вырожденную проекцию объекта, когда прямая проецируется в точку, а пл-ть – в линию. Полученные рез-ты обратным проецированием переносятся на заданные проекции.
Чтобы спроецировать прямую в точку, т.е. получить её вырожденную проекцию, следует выбрать направление проецирования, параллельное прямой (рис.41,а). Вырожденную проекцию пл-ти можно получить, если направление проецирования будет параллельным пл-ти (рис.41,б).
На рису. 41, в задача на пересечение прямой с пл-тью решена вспомогательным косоугольным проецированием на пл-ть Н. Направление проецирования выбрано параллельно стороне АВ тре-ка. Пл-ть тр-ка спроецировалась в прямую а1=d1e1. Обратным преобразованием полученная вспомогательная проекция точки пересенич
прямых MN и KL даст искомую проекцию ар точки A на плоскость Р по заданному направлению проецирования S. Чтобы получить неискаженную косоугольную проекцию, плоскость Р следует совместить с плоскостью чертежа. На рис. 47 все построения выполнены на эпюре. Совмещенное положение следа Ph 0 определено с помощью точки 1. Совмещенное положение прямых MN и KL получено перемещением точек т и k, в которых плоскости Q и Т пересекают след Ph, на совмещенное положение следа Ph 0. Совмещенное положение точки ар находится пересечением совмещенных прямых k 0 l' и m 0 n'. Сущность комбинированного способа и целесообразность его применения могут быть легко выяснены на примере определения точки встречи прямой с плоскостью. Эта задача чрезвычайно распространена, а подчас она является "ключом" при решении более сложных вопросов начертательной геометрии. Обычно при решении этой задачи в системе двух взаимно перпендикулярных плоскостей проекций Н и V мы получим две ортогональные проекции точки встречи прямой с плоскостью. Практически больший смысл представляет зафиксировать положение найденной точки не относительно плоскостей Н и V, а непосредственно на плоскости Р. Комбинированный способ дает возможность получить именно такой ответ.
14.Многогранником называют пространственное тело,поверхность которого образованна пересекающимися многоугольниками.Грань-поверхность ограниченная одним многоугольником.При пересечении граней образуются ребра, они пересекаются в вершинах многограника.
Развертка многог-ка –плоская фигура,образованная разложением всех граней на плоскость одной из них.Разложение производится вращением граней вокруг общих ребер
Б)Построение линии пересечения многограника с заданной плоскостью строится по точкам пересечения ребер сданной плоскостью.ПОСТРОЕНИЕ стр 19-20.глава 2
Построение точек пересечения прямой с поверхностью многограника можно осуществить путем введения вспомогательной секущей плоскости,которая проходит через заданную прямую.Пересечение многогранников плоскостью.Пример конструирования устойчивой подставки в виде усеченной пирамиды показан на рис. 6.4. Наклонная площадка ABCD образована срезом верхней части пирамиды фронтально- проецирующей плоскостью S (S2). Фронтальные проекции a2, b2, c2, d2 точек находятся на фронтальном следе S2 плоскости, а фронтальная проекция площадки ABCD совпадает со следом S2. Профильная a3b3c3d3 и горизонтальная a1b1c1d1проекции площадки построены по проекциям указанных точек на проекциях соответствующих ребер.
пересечение Прямой линии с многогранником
Для определения точек пересечения прямой линии с многогранником, задача сводится к нахождению точек пересечения прямой с
10. Способы преобразования проекций:
Способы преобразования предназначены гл.образом для решения метрических задач, связанных с определением дествит-х размеров и формы изобр-ых на эпюре геометр. объектов.
Основные способы преобразования проекций:
а) способ замены пл-тей проекции
б) способ вращения
в) способ косоугольного вспомогательного проецирования.
Новые проекции точек и осей проекций обозначают теми же буквами, но с цифровым индексом внизу, который опр-т последова-ть преобразований.
Способ косоугольного вспомог.проецирования.
Способы решения задач применяют при решении как метрических, так и позиционных задач. Сущность этого способа закл-ся в применении не прямоугольного, а косоугольного проецирования. Направление проецирование выбирается т.о., чтобы получить вырожденную проекцию объекта, когда прямая проецируется в точку, а пл-ть – в линию. Полученные рез-ты обратным проецированием переносятся на заданные проекции.
Чтобы спроецировать прямую в точку, т.е. получить её вырожденную проекцию, следует выбрать направление проецирования, параллельное прямой (рис.41,а). Вырожденную проекцию пл-ти можно получить, если направление проецирования будет параллельным пл-ти (рис.41,б).
На рису. 41, в задача на пересечение прямой с пл-тью решена вспомогательным косоугольным проецированием на пл-ть Н. Направление проецирования выбрано параллельно стороне АВ тре-ка. Пл-ть тр-ка спроецировалась в прямую а1=d1e1. Обратным преобразованием полученная вспомогательная проекция точки пересенич
прямых MN и KL даст искомую проекцию ар точки A на плоскость Р по заданному направлению проецирования S. Чтобы получить неискаженную косоугольную проекцию, плоскость Р следует совместить с плоскостью чертежа. На рис. 47 все построения выполнены на эпюре. Совмещенное положение следа Ph 0 определено с помощью точки 1. Совмещенное положение прямых MN и KL получено перемещением точек т и k, в которых плоскости Q и Т пересекают след Ph, на совмещенное положение следа Ph 0. Совмещенное положение точки ар находится пересечением совмещенных прямых k 0 l' и m 0 n'. Сущность комбинированного способа и целесообразность его применения могут быть легко выяснены на примере определения точки встречи прямой с плоскостью. Эта задача чрезвычайно распространена, а подчас она является "ключом" при решении более сложных вопросов начертательной геометрии. Обычно при решении этой задачи в системе двух взаимно перпендикулярных плоскостей проекций Н и V мы получим две ортогональные проекции точки встречи прямой с плоскостью. Практически больший смысл представляет зафиксировать положение найденной точки не относительно плоскостей Н и V, а непосредственно на плоскости Р. Комбинированный способ дает возможность получить именно такой ответ.
14.Многогранником называют пространственное тело,поверхность которого образованна пересекающимися многоугольниками.Грань-поверхность ограниченная одним многоугольником.При пересечении граней образуются ребра, они пересекаются в вершинах многограника.
Развертка многог-ка –плоская фигура,образованная разложением всех граней на плоскость одной из них.Разложение производится вращением граней вокруг общих ребер
Б)Построение линии пересечения многограника с заданной плоскостью строится по точкам пересечения ребер сданной плоскостью.ПОСТРОЕНИЕ стр 19-20.глава 2
Построение точек пересечения прямой с поверхностью многограника можно осуществить путем введения вспомогательной секущей плоскости,которая проходит через заданную прямую.Пересечение многогранников плоскостью.Пример конструирования устойчивой подставки в виде усеченной пирамиды показан на рис. 6.4. Наклонная площадка ABCD образована срезом верхней части пирамиды фронтально- проецирующей плоскостью S (S2). Фронтальные проекции a2, b2, c2, d2 точек находятся на фронтальном следе S2 плоскости, а фронтальная проекция площадки ABCD совпадает со следом S2. Профильная a3b3c3d3 и горизонтальная a1b1c1d1проекции площадки построены по проекциям указанных точек на проекциях соответствующих ребер.
пересечение Прямой линии с многогранником
Для определения точек пересечения прямой линии с многогранником, задача сводится к нахождению точек пересечения прямой с  плоскостями граней (рис.78).
Алгоритм решения задачи:
Алгоритм решения задачи:
1. Через заданную прямую mпроводим вспомогательную секущую плоскость (m).
2. Строим сечение многогранника с вспомогательной секущей плоскостью .
3. Определить искомые точки К,М - пересечения полученного сечения с прямой m.
4. Определить видимость прямой по отношению к пирамиде. плоскостями граней (рис.78).
Алгоритм решения задачи:
Алгоритм решения задачи:
1. Через заданную прямую mпроводим вспомогательную секущую плоскость (m).
2. Строим сечение многогранника с вспомогательной секущей плоскостью .
3. Определить искомые точки К,М - пересечения полученного сечения с прямой m.
4. Определить видимость прямой по отношению к пирамиде.
  б) эпюр
Рисунок 78. Пересечение прямой линии с пирамидой
18..Плоские кривые. Свойства. Проекции плоских кривых. Цепная линия.
Наиболее распространенными являются кривые линии. Для исследования локальных свойств плоской кривой строят в некоторой точке касательную и нормаль.
Касательной к плоской кривой в некоторой её точке называется предельное положение секущей, когда две общие с кривой точки сечения, стремясь друг к другу, совпадут. Касательная определяет направление движения точки по кривой.
Нормалью называется прямая, лежащая в плоскости кривой и перпендикулярная касательной в точке её касательная.
При решении некоторых задач приходится проводить касательную к кривой.
Свойства:
Точка кривой, в которой можно провести единственную касательную, называется гладкой. Кривая, состоящая только из одних гладких точек, называется гладкой кривой. Точка кривой называется обыкновенной, если при движении точки по кривой направление ее движения и направление поворота касательной не изменяются. Точки, не отвечающие этим требованием, называются особыми
Проекции плоских кривых.
Важное значение имеют некоторые кривые второго порядка- эллипс, парабола, гипербола.
Эллипс представляет собой множество точек, сумма расстояний от каждой из которых до двух данных точек (фокусов) есть величина постоянная: |МF1| + |MF2| = 2a.
Окружность– замкнутая плоская кривая, все точки которой одинаково удалены от данной точки (центра). Если R - радиус окружности - расстояние каждой его точки до центра, то длина окружности выразится числом 2pR, а площадь ею ограниченная, числом pR2, где p - отношение длины окружности к её диаметру.
Гипербола представляет собой множество точек, разность расстояния до двух данных точек (фокуса) есть величина постоянная: |МF1| - |MF2| = 2a.
Параболой называется геометрическое место точек, для каждой из которых расстояние до некоторой фиксированной точки плоскости, называемой фокусом, равно расстоянию до некоторой фиксированной прямой, называемой директрисой. Фокус параболы обозначается буквой F, расстояние от фокуса до директрисы - буквой р. Число р называется параметром параболы.
линия пересечения круглого конуса плоскостью, параллельной какой-либо касательной плоскости этого конуса. П. может быть также определена как геометрическое место точек плоскости, для каждой из которых расстояние до определённой точки F плоскости — фокуса П.— равно расстоянию до некоторой прямой MN — директрисы П. Прямая, проходящая через фокус перпендикулярно директрисе и направленная от директрисы к фокусу, называется осью П., а точка пересечения оси с П.— вершиной П.
Величина р называется параметром П. Парабола — линия второго порядка. Если в фокусе П. поместить источник света, то лучи, отразившиеся от П., образуют параллельный пучок, т.к. прямая PF, соединяющая любую точку Р П. с фокусом, и прямая, параллельная оси, образует с нормалью PR равные углы. Это свойство П. применяется, например, для прожекторных устройств.
Цепна́я ли́ния — линия, форму которой принимает гибкая однородная нерастяжимая тяжелая нить или цепь (отсюда название) с закрепленными концами в однородном гравитационном поле. Является плоской трансцендентной кривой
Перевёрнутая цепная линия — идеальная форма для арок. Однородная арка в форме перевёрнутой цепной линии испытывает только деформации сжатия, но не излома.
Горбатый мост имеет форму, близкую к цепной линии.
Стоит заметить, что цепь подвесного моста имеет форму параболы, а не цепной линии. Это связано с тем, что пролёт моста намного тяжелее цепи.
22.Пересечение прямой линии с кривой поверхностью.
Для построения точек пересечения прямой с кривой поверхностью следует через прямую провести
вспомогательную плоскость, найти линию пересечения этой плоскости с поверхностью. Точки пересе-
чения заданной прямой и построенной линии будут искомыми точками пересечения прямой с поверх-
ностью. Вспомогательную плоскость, проводимую через прямую, следует выбирать так, чтобы получа-
лись простые сечения (сечения, которые можно построить с помощью линейки и циркуля).
Пример 1. Построить точки пересечения прямой с поверхностью конуса
б) эпюр
Рисунок 78. Пересечение прямой линии с пирамидой
18..Плоские кривые. Свойства. Проекции плоских кривых. Цепная линия.
Наиболее распространенными являются кривые линии. Для исследования локальных свойств плоской кривой строят в некоторой точке касательную и нормаль.
Касательной к плоской кривой в некоторой её точке называется предельное положение секущей, когда две общие с кривой точки сечения, стремясь друг к другу, совпадут. Касательная определяет направление движения точки по кривой.
Нормалью называется прямая, лежащая в плоскости кривой и перпендикулярная касательной в точке её касательная.
При решении некоторых задач приходится проводить касательную к кривой.
Свойства:
Точка кривой, в которой можно провести единственную касательную, называется гладкой. Кривая, состоящая только из одних гладких точек, называется гладкой кривой. Точка кривой называется обыкновенной, если при движении точки по кривой направление ее движения и направление поворота касательной не изменяются. Точки, не отвечающие этим требованием, называются особыми
Проекции плоских кривых.
Важное значение имеют некоторые кривые второго порядка- эллипс, парабола, гипербола.
Эллипс представляет собой множество точек, сумма расстояний от каждой из которых до двух данных точек (фокусов) есть величина постоянная: |МF1| + |MF2| = 2a.
Окружность– замкнутая плоская кривая, все точки которой одинаково удалены от данной точки (центра). Если R - радиус окружности - расстояние каждой его точки до центра, то длина окружности выразится числом 2pR, а площадь ею ограниченная, числом pR2, где p - отношение длины окружности к её диаметру.
Гипербола представляет собой множество точек, разность расстояния до двух данных точек (фокуса) есть величина постоянная: |МF1| - |MF2| = 2a.
Параболой называется геометрическое место точек, для каждой из которых расстояние до некоторой фиксированной точки плоскости, называемой фокусом, равно расстоянию до некоторой фиксированной прямой, называемой директрисой. Фокус параболы обозначается буквой F, расстояние от фокуса до директрисы - буквой р. Число р называется параметром параболы.
линия пересечения круглого конуса плоскостью, параллельной какой-либо касательной плоскости этого конуса. П. может быть также определена как геометрическое место точек плоскости, для каждой из которых расстояние до определённой точки F плоскости — фокуса П.— равно расстоянию до некоторой прямой MN — директрисы П. Прямая, проходящая через фокус перпендикулярно директрисе и направленная от директрисы к фокусу, называется осью П., а точка пересечения оси с П.— вершиной П.
Величина р называется параметром П. Парабола — линия второго порядка. Если в фокусе П. поместить источник света, то лучи, отразившиеся от П., образуют параллельный пучок, т.к. прямая PF, соединяющая любую точку Р П. с фокусом, и прямая, параллельная оси, образует с нормалью PR равные углы. Это свойство П. применяется, например, для прожекторных устройств.
Цепна́я ли́ния — линия, форму которой принимает гибкая однородная нерастяжимая тяжелая нить или цепь (отсюда название) с закрепленными концами в однородном гравитационном поле. Является плоской трансцендентной кривой
Перевёрнутая цепная линия — идеальная форма для арок. Однородная арка в форме перевёрнутой цепной линии испытывает только деформации сжатия, но не излома.
Горбатый мост имеет форму, близкую к цепной линии.
Стоит заметить, что цепь подвесного моста имеет форму параболы, а не цепной линии. Это связано с тем, что пролёт моста намного тяжелее цепи.
22.Пересечение прямой линии с кривой поверхностью.
Для построения точек пересечения прямой с кривой поверхностью следует через прямую провести
вспомогательную плоскость, найти линию пересечения этой плоскости с поверхностью. Точки пересе-
чения заданной прямой и построенной линии будут искомыми точками пересечения прямой с поверх-
ностью. Вспомогательную плоскость, проводимую через прямую, следует выбирать так, чтобы получа-
лись простые сечения (сечения, которые можно построить с помощью линейки и циркуля).
Пример 1. Построить точки пересечения прямой с поверхностью конуса
  Пример 2. Построить точки пересечения прямой с поверхностью сферы
Пример 2. Построить точки пересечения прямой с поверхностью сферы
 26.Плоские кривые. Свойства проекции плоских кривых. Цепная линия.
П л о с к и е к р и в ы е
Плоские кривые имеют касательную, нормаль и кривизну.
Касательной называется предельное положение секущей, когда две общие с кривой точки стремятся друг к другу и совпадут в одной точке. Касательная – это прямая, имеющая общую точку с кривой. Нормалью называется прямая, лежащая в плоскости кривой и перпендикулярная касательной в точке ее касания. Кривизной плоской кривой в данной точке называется величина, обратная радиусу соприкасающейся окружности (r) Основные виды плоской кривой: окружност
26.Плоские кривые. Свойства проекции плоских кривых. Цепная линия.
П л о с к и е к р и в ы е
Плоские кривые имеют касательную, нормаль и кривизну.
Касательной называется предельное положение секущей, когда две общие с кривой точки стремятся друг к другу и совпадут в одной точке. Касательная – это прямая, имеющая общую точку с кривой. Нормалью называется прямая, лежащая в плоскости кривой и перпендикулярная касательной в точке ее касания. Кривизной плоской кривой в данной точке называется величина, обратная радиусу соприкасающейся окружности (r) Основные виды плоской кривой: окружност
|
Поиск по сайту:
|


 6. Взаимное положение плоскостей.Две пл-ти в пространстве могут быть либо параллельными, либо пересекающимися. Взаимно перпендикулярные пл-ти представляют собой частный случай пересекающихся пл-тей. Построение взаимно параллельных пл-тей.две пл-ти параллельны, если двум пересекающимся прямым, лежащим в одной пл-ти, соответствуют две параллельные пересекающиеся прямые другой пл-ти. Если же пл-ти заданы следами, то о взаимной параллельности их в пространстве можно судить по параллельности их одноименных следов.Построение параллельных пл-тей на чертеже удобно выполнять с помощью главных линий плоскости - горизонталей и фронталей. Прямая линия пересечения двух пл-тей определяется двумя точками, каждая из которых принадлежит обеим пл-тям. Или одной точкой, принадлежащей двум пл-тям, и известным направлением линии. В обоих случаях задача заключается в нахождении точки, общей для двух пл-тей. Общий прием построения линии пересечения двух пл-тей заключается в следующем: вводят вспомог. пл-ть, строят линии пересечения вспомогательной пл-ти с двумя заданными и в пересечении построенных линий находят общую точку двух пл-тей. Для нахождения второй общей точки построение повторяют с помощью еще одной вспомогательной пл-ти. Однако о параллельности профильно проецирующих пл-тей в пр-ве можно судить, лишь построив их профильные следы. Пересечение двух пл-тей. Две пл-ти пересекаются по прямой линии, общей для обеих пл-тей. Положение прямой линии опр-ся положением двух принадлежащих ей точек. Следовательно, для построения линии пересечения двух пл-тей достаточно определить две точки, общие для обеих заданных пл-тей. Если пл-ти заданы следами, то наиболее рационально отметить точки, являющиеся точками пересечения их одноименных следов (точки M и N прямой MN - линии пересечения пл-тей P и Q). Сущность этого метода состоит в том, что обе заданные пл-ти пересекаются третьей (обычно пл-тью частного положения - горизонтальной или фронтальной), затем строятся линии пересечения первой заданной пл-ти с третьей, второй заданной с третьей. Там, где эти линии пересекаются, отмечается точка, общая для заданных пл-тей. Вторая общая точка находится при помощи еще одной вспомогательной плоскости
Пересекающиеся плоскости. Построение линии пересечения пл-тей — одна из основных задач нач. геометрии. Она относится к так называемым позиционным задачам.
Позиционными наз-т задачи на определение общих эл-тов различных сопрягаемых геом-ких форм
Две пл-ти пересекаются по прямой линии. Поэтому для построения линии пересечения пл-тей необходимо опр-ть две точки этой прямой.
Рассмотрим частный случай пересечения пл-тей, когда одна из них — проецирующая.
На рис. 23, а приведены пл-ть общего положения Р и горизонтально проецирующая плоскость S. Двумя общими точками, принадлежащими обеим плоскостям, являются точки пересечения М и N одноименных следов этих плоскостей, которые и определяют линию пересечения.
Однако линия пересечения плоскостей может быть определена и другим образом. Если одна из пересекающихся плоскостей проецирующая, то одна из проекций линии пересечения совпадает с ее проецирующим следом. Горизонтальная проекция пт линии пересечения заданных плоскостей лежит на горизонтальном следе SH горизонтально проецирующей плоскости S. Фронтальная проекция линии пересечения определяется линиями связи.
На рис. 23, б показаны плоскость общего положения, заданная треугольником ABC, и фронтально проецирующая плоскость S. На фронтальной проекции в пересечении проецирующего следа плоскости Sv со сторонами треугольника получим две общие точки I' и 2' и фронтальную проекцию линии пересечения плоскостей. Горизонтальная проекция определяется с помощью про-ведения линии связи.
Рассмотрим общий случай пересечения, когда обе плоскости — общего положения. На рис. 24 приведены две плоскости, заданные следами. Как и в предыдущем примере, общими точками плоскостей являются точки пересечения М и N одноименных следов. Соединяя одноименные проекции этих точек прямой линией, получим проекции линии пересечения плоскостей.
Если точки пересечения одноименных следов находятся вне поля чертежа, а также в тех случаях, когда плоскости заданы не следами, а другими геометрическими элементами, то для оп-ределения линии пересечения плоскостей следует использовать вспомогательные плоскости уровня — горизонтальные или фронтальные.
На рис. 25 показаны две плоскости общего положения, заданные треугольником и двумя параллельными прямыми. Для определения двух общих точек линии пересечения плоскостей прово-дим две вспомогательные (горизонтальные) плоскости уровня S и Т. Вспомогательная плоскость S пересекает заданные плоскости по двум горизонталям й„ которые в своем пересечении определяют точку /, общую для плоскостей Р и Q, так как они одновременно принадлежат вспомогательной секущей плоскости S. Вторая вспомогательная плоскость Т также пересекает каждую из заданных плоскостей по горизонталям hp которые параллельны первым двум
горизонталям. В пересечении горизонталей получим вторую общую точку II заданных плоскостей. Соединяя на эпюре одноименные проекции этих точек, получим проекции линии пересечения плоскостей.
Необходимо отметить, что при построении линии пересечения плоскостей, заданных следами в предыдущем примере (см. рис. 24), роль вспомогательных секущих плоскостей выполняют плоскости проекций Я и V.
6. Взаимное положение плоскостей.Две пл-ти в пространстве могут быть либо параллельными, либо пересекающимися. Взаимно перпендикулярные пл-ти представляют собой частный случай пересекающихся пл-тей. Построение взаимно параллельных пл-тей.две пл-ти параллельны, если двум пересекающимся прямым, лежащим в одной пл-ти, соответствуют две параллельные пересекающиеся прямые другой пл-ти. Если же пл-ти заданы следами, то о взаимной параллельности их в пространстве можно судить по параллельности их одноименных следов.Построение параллельных пл-тей на чертеже удобно выполнять с помощью главных линий плоскости - горизонталей и фронталей. Прямая линия пересечения двух пл-тей определяется двумя точками, каждая из которых принадлежит обеим пл-тям. Или одной точкой, принадлежащей двум пл-тям, и известным направлением линии. В обоих случаях задача заключается в нахождении точки, общей для двух пл-тей. Общий прием построения линии пересечения двух пл-тей заключается в следующем: вводят вспомог. пл-ть, строят линии пересечения вспомогательной пл-ти с двумя заданными и в пересечении построенных линий находят общую точку двух пл-тей. Для нахождения второй общей точки построение повторяют с помощью еще одной вспомогательной пл-ти. Однако о параллельности профильно проецирующих пл-тей в пр-ве можно судить, лишь построив их профильные следы. Пересечение двух пл-тей. Две пл-ти пересекаются по прямой линии, общей для обеих пл-тей. Положение прямой линии опр-ся положением двух принадлежащих ей точек. Следовательно, для построения линии пересечения двух пл-тей достаточно определить две точки, общие для обеих заданных пл-тей. Если пл-ти заданы следами, то наиболее рационально отметить точки, являющиеся точками пересечения их одноименных следов (точки M и N прямой MN - линии пересечения пл-тей P и Q). Сущность этого метода состоит в том, что обе заданные пл-ти пересекаются третьей (обычно пл-тью частного положения - горизонтальной или фронтальной), затем строятся линии пересечения первой заданной пл-ти с третьей, второй заданной с третьей. Там, где эти линии пересекаются, отмечается точка, общая для заданных пл-тей. Вторая общая точка находится при помощи еще одной вспомогательной плоскости
Пересекающиеся плоскости. Построение линии пересечения пл-тей — одна из основных задач нач. геометрии. Она относится к так называемым позиционным задачам.
Позиционными наз-т задачи на определение общих эл-тов различных сопрягаемых геом-ких форм
Две пл-ти пересекаются по прямой линии. Поэтому для построения линии пересечения пл-тей необходимо опр-ть две точки этой прямой.
Рассмотрим частный случай пересечения пл-тей, когда одна из них — проецирующая.
На рис. 23, а приведены пл-ть общего положения Р и горизонтально проецирующая плоскость S. Двумя общими точками, принадлежащими обеим плоскостям, являются точки пересечения М и N одноименных следов этих плоскостей, которые и определяют линию пересечения.
Однако линия пересечения плоскостей может быть определена и другим образом. Если одна из пересекающихся плоскостей проецирующая, то одна из проекций линии пересечения совпадает с ее проецирующим следом. Горизонтальная проекция пт линии пересечения заданных плоскостей лежит на горизонтальном следе SH горизонтально проецирующей плоскости S. Фронтальная проекция линии пересечения определяется линиями связи.
На рис. 23, б показаны плоскость общего положения, заданная треугольником ABC, и фронтально проецирующая плоскость S. На фронтальной проекции в пересечении проецирующего следа плоскости Sv со сторонами треугольника получим две общие точки I' и 2' и фронтальную проекцию линии пересечения плоскостей. Горизонтальная проекция определяется с помощью про-ведения линии связи.
Рассмотрим общий случай пересечения, когда обе плоскости — общего положения. На рис. 24 приведены две плоскости, заданные следами. Как и в предыдущем примере, общими точками плоскостей являются точки пересечения М и N одноименных следов. Соединяя одноименные проекции этих точек прямой линией, получим проекции линии пересечения плоскостей.
Если точки пересечения одноименных следов находятся вне поля чертежа, а также в тех случаях, когда плоскости заданы не следами, а другими геометрическими элементами, то для оп-ределения линии пересечения плоскостей следует использовать вспомогательные плоскости уровня — горизонтальные или фронтальные.
На рис. 25 показаны две плоскости общего положения, заданные треугольником и двумя параллельными прямыми. Для определения двух общих точек линии пересечения плоскостей прово-дим две вспомогательные (горизонтальные) плоскости уровня S и Т. Вспомогательная плоскость S пересекает заданные плоскости по двум горизонталям й„ которые в своем пересечении определяют точку /, общую для плоскостей Р и Q, так как они одновременно принадлежат вспомогательной секущей плоскости S. Вторая вспомогательная плоскость Т также пересекает каждую из заданных плоскостей по горизонталям hp которые параллельны первым двум
горизонталям. В пересечении горизонталей получим вторую общую точку II заданных плоскостей. Соединяя на эпюре одноименные проекции этих точек, получим проекции линии пересечения плоскостей.
Необходимо отметить, что при построении линии пересечения плоскостей, заданных следами в предыдущем примере (см. рис. 24), роль вспомогательных секущих плоскостей выполняют плоскости проекций Я и V.


 9. Способы преобразования проекций:
Способы преобразования предназначены гл.образом для решения метрических задач, связанных с определением дествит-х размеров и формы изобр-ых на эпюре геометр. объектов.
Основные способы преобразования проекций:
а) способ замены пл-тей проекции
б) способ вращения
в) способ косоугольного вспомогательного проецирования.
Новые проекции точек и осей проекций обозначают теми же буквами, но с цифровым индексом внизу, который опр-т последова-ть преобразований.
Способ замены пл-тей проекций. Сущность способа замены пл-тей проекций заключается в том, что при неизменном положении объекта в пространстве производится замена данной системы плоскостей проекцией новой системой взаимно перпендикулярных пл-тей проекций (рис. 33, а). При переходе к новой системе одну из плоскостей проекций заменяют новой пл-тью таким образом, чтобы данный геометрический элемент (прямая, пл-ть) занял частное положение и проецировался без искажения.
При решении ряда метрических задач требуется преобразовать прямую общего положения в прямую уровня, а затем — в проецирующую, выполнив при этом последовательно два преобразования.
Рассмотрим ход решения этой задачи.
1-е преобразование (рис. 33, б). Для того чтобы прямая АВ спроецировалась линией уровня, следует ввести новую плоскость проекций и расположить ее параллельно данной прямой. При этом новая ось jc, будет параллельна одной из проекций прямой. На рис. 33, а, б ось проведена параллельно горизонтальной проекции ab, а новая плоскость проекций Vl расположена параллельно прямой АВ, которая проецируется на эту плоскость в истинную величину (новая фронтальная проекция прямой — а\Ь\). Новая ось х, и плоскость проекции V, могут быть расположены на любом расстоянии от прямой, они могут совпадать с прямой и ее проекцией.
При замене плоскостей проекций расстояние от новой проекции точки до новой оси равно расстоянию от заменяемой проекции точки до старой оси проекций. Иными словами, высоты (аппликаты) концов отрезка в новой системе плоскостей проекций останутся прежними. В результате этой замены определены действительная величина отрезка прямой и угол наклона а к пл-ти Н. При переходе к эпюру плоскость совмещается с плоскостью Н.
2-е преобразование (рис. 33, в). Для того чтобы прямая АВ оказалась проецирующей, т. е. изобразилась точкой, необходимо произвести вторую замену плоскости проекций и расположить новую плоскость Н, перпендикулярно прямой. Новая ось х2 выбрана на эпюре перпендикулярной новой фронтальной проекции прямой а'ХЪ\. На новой пл-ти проекций Ну прямая изобразится точкой, так как координаты концов отрезка в системе H1V1 одинаковы.
Т.о., прямая А В в системе HjVl стала проецирующей относительно пл-ти Н1.
Рассмотрим еще одну задачу — требуется определить истинную величину плоской фигуры — треугольника ABC, занимающего в пространстве общее положение. Для решения этой задачи необходимо преобразовать эпюр так, чтобы плоскость общего положения стала параллельной одной из плоскостей проекций новой системы. В ортогонально-проекционной системе решить эту задачу одной заменой плоскости проекций нельзя. Как и в предыдущей задаче, необходимо выполнить два преобразования, но в иной последовальности: сначала следует преобразовать плоскость общего положения в проецирующую, а затем — в плоскость уровня.
На рис. 34, а сначала заменена фронтальная плоскость проекций новой плоскостью F„ перпендикулярной плоскости треугольника. Это условие выполнено с помощью вспомогательной прямой — линии уровня, например, горизонтали AN (рис. 34, б). Новая ось хх проведена на эпюре перпендикулярно горизонтальной проекции горизонтали. На новой плоскости проекций У, горизонталь спроецировалась в точку, а плоскость треугольника — в линию.
Угол а определяет угол наклона треугольника к горизонтальной плоскости Н.
На втором этапе решения проведена вторая замена — новая плоскость проекций Я, установлена параллельно треугольнику. Новая ось х2 проведена параллельно новой фронтальной проекции треугольника — прямой b\a\d Построенная проекция определяет истинную величину и форму треугольника.
Если плоскость задана следами, а не плоской фигурой, ее следует преобразовать в проецирующую. Для этого новую плоскость проекций и новую ось проекций следует расположить перпен-дикулярно, например, к горизонтальному следу заданной плоскости (рис. 35),
при этом горизонтальный след спроецируется на новой плоскости в точку (Рх).
Для построения новой проекции фронтального следа Pv достаточно найти
проекцию любой точки заданной плоскости, например произвольной точки N, лежащей на следе. Прямая Р—п, является искомым проецирующим следом данной плоскости.
9. Способы преобразования проекций:
Способы преобразования предназначены гл.образом для решения метрических задач, связанных с определением дествит-х размеров и формы изобр-ых на эпюре геометр. объектов.
Основные способы преобразования проекций:
а) способ замены пл-тей проекции
б) способ вращения
в) способ косоугольного вспомогательного проецирования.
Новые проекции точек и осей проекций обозначают теми же буквами, но с цифровым индексом внизу, который опр-т последова-ть преобразований.
Способ замены пл-тей проекций. Сущность способа замены пл-тей проекций заключается в том, что при неизменном положении объекта в пространстве производится замена данной системы плоскостей проекцией новой системой взаимно перпендикулярных пл-тей проекций (рис. 33, а). При переходе к новой системе одну из плоскостей проекций заменяют новой пл-тью таким образом, чтобы данный геометрический элемент (прямая, пл-ть) занял частное положение и проецировался без искажения.
При решении ряда метрических задач требуется преобразовать прямую общего положения в прямую уровня, а затем — в проецирующую, выполнив при этом последовательно два преобразования.
Рассмотрим ход решения этой задачи.
1-е преобразование (рис. 33, б). Для того чтобы прямая АВ спроецировалась линией уровня, следует ввести новую плоскость проекций и расположить ее параллельно данной прямой. При этом новая ось jc, будет параллельна одной из проекций прямой. На рис. 33, а, б ось проведена параллельно горизонтальной проекции ab, а новая плоскость проекций Vl расположена параллельно прямой АВ, которая проецируется на эту плоскость в истинную величину (новая фронтальная проекция прямой — а\Ь\). Новая ось х, и плоскость проекции V, могут быть расположены на любом расстоянии от прямой, они могут совпадать с прямой и ее проекцией.
При замене плоскостей проекций расстояние от новой проекции точки до новой оси равно расстоянию от заменяемой проекции точки до старой оси проекций. Иными словами, высоты (аппликаты) концов отрезка в новой системе плоскостей проекций останутся прежними. В результате этой замены определены действительная величина отрезка прямой и угол наклона а к пл-ти Н. При переходе к эпюру плоскость совмещается с плоскостью Н.
2-е преобразование (рис. 33, в). Для того чтобы прямая АВ оказалась проецирующей, т. е. изобразилась точкой, необходимо произвести вторую замену плоскости проекций и расположить новую плоскость Н, перпендикулярно прямой. Новая ось х2 выбрана на эпюре перпендикулярной новой фронтальной проекции прямой а'ХЪ\. На новой пл-ти проекций Ну прямая изобразится точкой, так как координаты концов отрезка в системе H1V1 одинаковы.
Т.о., прямая А В в системе HjVl стала проецирующей относительно пл-ти Н1.
Рассмотрим еще одну задачу — требуется определить истинную величину плоской фигуры — треугольника ABC, занимающего в пространстве общее положение. Для решения этой задачи необходимо преобразовать эпюр так, чтобы плоскость общего положения стала параллельной одной из плоскостей проекций новой системы. В ортогонально-проекционной системе решить эту задачу одной заменой плоскости проекций нельзя. Как и в предыдущей задаче, необходимо выполнить два преобразования, но в иной последовальности: сначала следует преобразовать плоскость общего положения в проецирующую, а затем — в плоскость уровня.
На рис. 34, а сначала заменена фронтальная плоскость проекций новой плоскостью F„ перпендикулярной плоскости треугольника. Это условие выполнено с помощью вспомогательной прямой — линии уровня, например, горизонтали AN (рис. 34, б). Новая ось хх проведена на эпюре перпендикулярно горизонтальной проекции горизонтали. На новой плоскости проекций У, горизонталь спроецировалась в точку, а плоскость треугольника — в линию.
Угол а определяет угол наклона треугольника к горизонтальной плоскости Н.
На втором этапе решения проведена вторая замена — новая плоскость проекций Я, установлена параллельно треугольнику. Новая ось х2 проведена параллельно новой фронтальной проекции треугольника — прямой b\a\d Построенная проекция определяет истинную величину и форму треугольника.
Если плоскость задана следами, а не плоской фигурой, ее следует преобразовать в проецирующую. Для этого новую плоскость проекций и новую ось проекций следует расположить перпен-дикулярно, например, к горизонтальному следу заданной плоскости (рис. 35),
при этом горизонтальный след спроецируется на новой плоскости в точку (Рх).
Для построения новой проекции фронтального следа Pv достаточно найти
проекцию любой точки заданной плоскости, например произвольной точки N, лежащей на следе. Прямая Р—п, является искомым проецирующим следом данной плоскости.


 13. Многогранники – замкнутые пространственные фигуры, ограниченные плоскими многоугольниками. Многогранник называется метрически правильным, если все его грани являются правильными многоугольниками. К ним относятся куб, тетраэдр, октаэдр, икосаэдр, додекаэдр.Тетраэдр(четырехгранник) - ограничен четырьмя равносторонними и равными треугольниками.Гексаэдр(четырехгранник, или куб) - ограничен шестью равными квадратами. Октаэдр(восьмигранник) - ограничен восемью равносторонними и равными треугольниками. Додекаэдр(двенадцатигранник) - ограничен двенадцатью равносторонними и равными пятиугольниками. Икосаэдр(двадцатигранник) - ограничен двадцатью равносторонними и равными треугольниками.Пирамида- это многогранник, одна грань которого многоугольник, а остальные грани - треугольники с общей вершиной. Пирамида называется правильной, если в основании лежит правильный многоугольник и высота пирамиды проходит через центр многоугольника. Пирамида называется усеченной, если вершина её отсекается плоскостью (рис.6.1.).Призма- многоугольник, две грани которого (основания призмы) представляют собой равные многоугольники с взаимно параллельными сторонами, а все другие грани параллелограммы. Призма называется прямой, если её ребра перпендикулярны плоскости основания. Если основанием призмы является прямоугольник, призму называют параллелепипедом (рис 6.2.). Тетраэдр - правильный четырехгранник (рис 6.4.). Он ограничен четырьмя равносторонними треугольниками (это правильная треугольная пирамида).
17. Пересечение многогранных поверхностей.??? Взаимное пересечение поверхностейЛинией пересечения двух поверхностей является множество точек, общих для данных поверхностей. Из этого множества выделяют характерные (опорные, или главные) точки, с которых следует начинать построение этой линии. Они позволяют увидеть, в каких границах можно изменять положение вспомогательных секущих поверхностей для определения остальных точек.К таким точкам относятся: экстремальные точки- верхняя и нижняя точки относительно той или иной плоскости проекций; точки, расположенные на очерковых образующих некоторых поверхностей точки границы зоны видимости и т.д.Следует имеет в виду, что линия пересечения двух поверхностей в проекциях всегда располагается в пределах контура наложения проекций двух пересекающихся поверхностей.
Иногда целесообразно воспользоваться преобразованием чертежа, чтобы представить пересекающиеся поверхности (или одну из них) в частном положении.Для определения этих точек часто пользуются вспомогательными секущими поверхностями. Поверхности-посредники пересекают данные поверхности по линиям, которые, в свою очередь, пересекаются в точках линии пересечения данных поверхностей.Секущие поверхности-посредники выбираются так, чтобы они, пересекаясь с данными поверхностями, давали простые для построения линии, например прямые и окружности.Из общей схемы построения линии пересечения поверхностей выделяют два основных метода - метод секущих плоскостей и метод секущих сфер.В общем случае решение задачи по построении линии пересечения двух поверхностей может быть сведено к рассмотренным ранее задачам по определению:
1. Точек пересечения линии с поверхностью;
2. Линии пересечения плоскости и поверхности;
3. Комбинации первой и второй задачи.
21.
21.Кривые поверхности. Классификация поверхностей.
Кривой поверхностью называется совокупность последовательных положений линии (образующей), движущейся в пространстве по некоторому закону.
Закон движения образующей определяется неподвижными направляющими элементами и положением образующей относительно этих элементов в любой момент движения. Таким образом, определителем кривой поверхности является:
1. Образующая (прямая или кривая линия);
2. Направляющие элементы (точки, прямые, кривые линии, плоскости);
3. Условия, определяющие положение образующей относительно направляющих элементов.
Например, коническая поверхность (рис. 10, а) образуется движением прямой линии l, которая в каждый момент движения пересекает кривую линию m и проходит через неподвижную точку S. Здесь l – образующая, m и S – направляющие. Условная запись определителя поверхности: q (l,m, S; l ∩ m; l ' S).
Построение проекций кривой поверхностисводится к построению проекций параметров определителя (рис. 10, б) или очерков проекций.
Построение точки, принадлежащей кривой поверхности: на заданной поверхности провести какую-либо по возможности простейшую линию (образующую, параллель…) и на ней задать точку. На рис. 10, в точка А принадлежит направляющей m, точка К принадлежит образующей SА.
Классификация поверхностей.
Из большего числа возможных способов образования поверхностей рассмотрим основные способы, выделив главные признаки их классификации.
1. По закону движения образующей-поверхности с поступательным движением образующей, с вращательным и винтовым движением образующей.
2. По виду образующей различают поверхности с прямолинейной образующей- линейчатые и поверхности с криволинейной образующей - нелинейчатые
3. По закону изменения формы образующей – с образующей постоянного или переменного вида.
4. По признаку развертывания поверхности на плоскость – развертываемые и неразвертываемые.
5. По способу задания поверхности – аналитическому или графическому.
6. По дифференциальным свойствам – гладкие или не гладкие поверхности и по признаку кривизны поверхности
Необходимо отметить, что одни и те же поверхности могут быть классифицированы по различным признакам.
25.Теоретические основы построения теней в ортогональных проекциях. Направление световых лучей (тень от точки)
Назначение теней.
Тени строят на фасадах зданий и сооружений, на планах застройки района или
квартала для придания чертежу наглядности и выразительности. Построение теней выполняется для выявления освещенности отдельных элементов проектируемого здания или сооружения.
По форме и размерам тени можно определить форму и размеры предмета, отбрасывающего тень.
Основная задача теории теней
Основная задача теории теней – определение контуров собственной и
падающей тени данного объекта. Собственная тень – неосвещенная часть поверхности предмета.
Падающая тень – тень, отбрасываемая предметом на плоскости проекций и другие предметы.
Каждой точке контура собственной тени соответствует определенная точка контура падающей тени.
Основные понятия
Освещение предмета может быть факельным, если источник света удален от предмета на незначительное расстояние. Освещение предмета может быть солнечным, если источник света удален в бесконечность. При таком освещении:
* источник света – Солнце - удален в бесконечность;
* световые лучи распространяются прямолинейно;
* световые лучи параллельны друг другу.
За направление световых лучей S принимают направление одной из диагоналей куба, грани которого параллельны плоскостям проекций. Ортогональные проекции луча S на плоскости проекций составляют с осями координат угол 45°.
тени от точки
Иногда возникает необходимость построить тень точки, которой в действительности нет. Такую тень
называют мнимой (смотри страницу 12,26, 28). А т – действительная (реальная) тень точки А
на фронтальную плоскость проекций А T м – мнимая (воображаемая) тень точки А на горизонтальную плоскость проекций. Построение А T м видно из чертежа.
13. Многогранники – замкнутые пространственные фигуры, ограниченные плоскими многоугольниками. Многогранник называется метрически правильным, если все его грани являются правильными многоугольниками. К ним относятся куб, тетраэдр, октаэдр, икосаэдр, додекаэдр.Тетраэдр(четырехгранник) - ограничен четырьмя равносторонними и равными треугольниками.Гексаэдр(четырехгранник, или куб) - ограничен шестью равными квадратами. Октаэдр(восьмигранник) - ограничен восемью равносторонними и равными треугольниками. Додекаэдр(двенадцатигранник) - ограничен двенадцатью равносторонними и равными пятиугольниками. Икосаэдр(двадцатигранник) - ограничен двадцатью равносторонними и равными треугольниками.Пирамида- это многогранник, одна грань которого многоугольник, а остальные грани - треугольники с общей вершиной. Пирамида называется правильной, если в основании лежит правильный многоугольник и высота пирамиды проходит через центр многоугольника. Пирамида называется усеченной, если вершина её отсекается плоскостью (рис.6.1.).Призма- многоугольник, две грани которого (основания призмы) представляют собой равные многоугольники с взаимно параллельными сторонами, а все другие грани параллелограммы. Призма называется прямой, если её ребра перпендикулярны плоскости основания. Если основанием призмы является прямоугольник, призму называют параллелепипедом (рис 6.2.). Тетраэдр - правильный четырехгранник (рис 6.4.). Он ограничен четырьмя равносторонними треугольниками (это правильная треугольная пирамида).
17. Пересечение многогранных поверхностей.??? Взаимное пересечение поверхностейЛинией пересечения двух поверхностей является множество точек, общих для данных поверхностей. Из этого множества выделяют характерные (опорные, или главные) точки, с которых следует начинать построение этой линии. Они позволяют увидеть, в каких границах можно изменять положение вспомогательных секущих поверхностей для определения остальных точек.К таким точкам относятся: экстремальные точки- верхняя и нижняя точки относительно той или иной плоскости проекций; точки, расположенные на очерковых образующих некоторых поверхностей точки границы зоны видимости и т.д.Следует имеет в виду, что линия пересечения двух поверхностей в проекциях всегда располагается в пределах контура наложения проекций двух пересекающихся поверхностей.
Иногда целесообразно воспользоваться преобразованием чертежа, чтобы представить пересекающиеся поверхности (или одну из них) в частном положении.Для определения этих точек часто пользуются вспомогательными секущими поверхностями. Поверхности-посредники пересекают данные поверхности по линиям, которые, в свою очередь, пересекаются в точках линии пересечения данных поверхностей.Секущие поверхности-посредники выбираются так, чтобы они, пересекаясь с данными поверхностями, давали простые для построения линии, например прямые и окружности.Из общей схемы построения линии пересечения поверхностей выделяют два основных метода - метод секущих плоскостей и метод секущих сфер.В общем случае решение задачи по построении линии пересечения двух поверхностей может быть сведено к рассмотренным ранее задачам по определению:
1. Точек пересечения линии с поверхностью;
2. Линии пересечения плоскости и поверхности;
3. Комбинации первой и второй задачи.
21.
21.Кривые поверхности. Классификация поверхностей.
Кривой поверхностью называется совокупность последовательных положений линии (образующей), движущейся в пространстве по некоторому закону.
Закон движения образующей определяется неподвижными направляющими элементами и положением образующей относительно этих элементов в любой момент движения. Таким образом, определителем кривой поверхности является:
1. Образующая (прямая или кривая линия);
2. Направляющие элементы (точки, прямые, кривые линии, плоскости);
3. Условия, определяющие положение образующей относительно направляющих элементов.
Например, коническая поверхность (рис. 10, а) образуется движением прямой линии l, которая в каждый момент движения пересекает кривую линию m и проходит через неподвижную точку S. Здесь l – образующая, m и S – направляющие. Условная запись определителя поверхности: q (l,m, S; l ∩ m; l ' S).
Построение проекций кривой поверхностисводится к построению проекций параметров определителя (рис. 10, б) или очерков проекций.
Построение точки, принадлежащей кривой поверхности: на заданной поверхности провести какую-либо по возможности простейшую линию (образующую, параллель…) и на ней задать точку. На рис. 10, в точка А принадлежит направляющей m, точка К принадлежит образующей SА.
Классификация поверхностей.
Из большего числа возможных способов образования поверхностей рассмотрим основные способы, выделив главные признаки их классификации.
1. По закону движения образующей-поверхности с поступательным движением образующей, с вращательным и винтовым движением образующей.
2. По виду образующей различают поверхности с прямолинейной образующей- линейчатые и поверхности с криволинейной образующей - нелинейчатые
3. По закону изменения формы образующей – с образующей постоянного или переменного вида.
4. По признаку развертывания поверхности на плоскость – развертываемые и неразвертываемые.
5. По способу задания поверхности – аналитическому или графическому.
6. По дифференциальным свойствам – гладкие или не гладкие поверхности и по признаку кривизны поверхности
Необходимо отметить, что одни и те же поверхности могут быть классифицированы по различным признакам.
25.Теоретические основы построения теней в ортогональных проекциях. Направление световых лучей (тень от точки)
Назначение теней.
Тени строят на фасадах зданий и сооружений, на планах застройки района или
квартала для придания чертежу наглядности и выразительности. Построение теней выполняется для выявления освещенности отдельных элементов проектируемого здания или сооружения.
По форме и размерам тени можно определить форму и размеры предмета, отбрасывающего тень.
Основная задача теории теней
Основная задача теории теней – определение контуров собственной и
падающей тени данного объекта. Собственная тень – неосвещенная часть поверхности предмета.
Падающая тень – тень, отбрасываемая предметом на плоскости проекций и другие предметы.
Каждой точке контура собственной тени соответствует определенная точка контура падающей тени.
Основные понятия
Освещение предмета может быть факельным, если источник света удален от предмета на незначительное расстояние. Освещение предмета может быть солнечным, если источник света удален в бесконечность. При таком освещении:
* источник света – Солнце - удален в бесконечность;
* световые лучи распространяются прямолинейно;
* световые лучи параллельны друг другу.
За направление световых лучей S принимают направление одной из диагоналей куба, грани которого параллельны плоскостям проекций. Ортогональные проекции луча S на плоскости проекций составляют с осями координат угол 45°.
тени от точки
Иногда возникает необходимость построить тень точки, которой в действительности нет. Такую тень
называют мнимой (смотри страницу 12,26, 28). А т – действительная (реальная) тень точки А
на фронтальную плоскость проекций А T м – мнимая (воображаемая) тень точки А на горизонтальную плоскость проекций. Построение А T м видно из чертежа.
 Тень точки
Падающая тень точки является точкой пересечения светового луча S, проходящего через нее, с
поверхностью или плоскостью, а которую падает тень. Тень точки упадет на ту плоскость проекций, которую световой луч встретит раньше, то есть к которой точка располагается ближе.Построение тени точки способом равнобедренного прямоугольного треугольника
Можно построить тень точки, не проводя световые лучи, а формируя прямоугольный равнобедренный треугольник по направлению светового луча, как показано на чертеже.
Тень точки
Падающая тень точки является точкой пересечения светового луча S, проходящего через нее, с
поверхностью или плоскостью, а которую падает тень. Тень точки упадет на ту плоскость проекций, которую световой луч встретит раньше, то есть к которой точка располагается ближе.Построение тени точки способом равнобедренного прямоугольного треугольника
Можно построить тень точки, не проводя световые лучи, а формируя прямоугольный равнобедренный треугольник по направлению светового луча, как показано на чертеже.




 .
7. Взаимное положение прямой линии и плоскости.
Прямая может находиться в пл-ти, быть параллельной ей или пересекать пл-ть.
При пересечении прямой линии с пл-тью следует выделить частный случай, когда прямая перпенд. пл-ти.
Прямая перпендикулярная пл-ти, если её проекции перпендикулярны одноименным следам пл-ти или соответствующим проекциям горизонтали и фронтали.
(рис. 31). На рис. 31, а, б показана прямая АВ, перпендикулярная пл-ти Р, заданной следами. Проведем в пл-ти Р через точку В горизонталь. На основе правила проецирования прямого угла,угол, образованный перпендикуляром А В и горизонталью, будет проецироваться на пл-ти Н прямым (abn=90°). Аналогичный вывод можно сделать и в отношении фронтальной проекции перпендикуляра.
Для того чтобы построить прямую, перпендикулярную пл-ти, заданной треугольником BCD (рис. 31, в), не следует строить следы пл-ти. Необходимо сначала построить в пл-ти горизонталь и фронталь, а затем провести проекции перпендикуляра под прямым углом к одноименным проекциям горизонтали и фронтали.
Т.о., если прямая перпендикулярна двум пересекающимся прямым, принадлежащим пл-ти,
то она перпендикулярна и самой пл-ти.
Приведенное положение дает возможность решать ряд задач и, в частности, опустить или восставить перпендикуляр к пл-ти, решить обратную задачу — провести плоскость перпендикулярно прямой, определить расстояние от точки до пл-ти.
Пусть требуется определить расстояние от точки до пл-ти. Иными словами, необходимо определить длину перпендикуляра, опущенного из данной точки на пл-ть.Задача решается в три этапа, каждый из которых представляет собой одну из рассмотренных ранее задач: 1) определить направление проекций перпендикуляра к пл-ти; 2) построить точку пересечения прямой (перпендикуляра) с пл-тью; 3) определить длину перпендикуляра способом прямоугольного треугольника.
.
7. Взаимное положение прямой линии и плоскости.
Прямая может находиться в пл-ти, быть параллельной ей или пересекать пл-ть.
При пересечении прямой линии с пл-тью следует выделить частный случай, когда прямая перпенд. пл-ти.
Прямая перпендикулярная пл-ти, если её проекции перпендикулярны одноименным следам пл-ти или соответствующим проекциям горизонтали и фронтали.
(рис. 31). На рис. 31, а, б показана прямая АВ, перпендикулярная пл-ти Р, заданной следами. Проведем в пл-ти Р через точку В горизонталь. На основе правила проецирования прямого угла,угол, образованный перпендикуляром А В и горизонталью, будет проецироваться на пл-ти Н прямым (abn=90°). Аналогичный вывод можно сделать и в отношении фронтальной проекции перпендикуляра.
Для того чтобы построить прямую, перпендикулярную пл-ти, заданной треугольником BCD (рис. 31, в), не следует строить следы пл-ти. Необходимо сначала построить в пл-ти горизонталь и фронталь, а затем провести проекции перпендикуляра под прямым углом к одноименным проекциям горизонтали и фронтали.
Т.о., если прямая перпендикулярна двум пересекающимся прямым, принадлежащим пл-ти,
то она перпендикулярна и самой пл-ти.
Приведенное положение дает возможность решать ряд задач и, в частности, опустить или восставить перпендикуляр к пл-ти, решить обратную задачу — провести плоскость перпендикулярно прямой, определить расстояние от точки до пл-ти.
Пусть требуется определить расстояние от точки до пл-ти. Иными словами, необходимо определить длину перпендикуляра, опущенного из данной точки на пл-ть.Задача решается в три этапа, каждый из которых представляет собой одну из рассмотренных ранее задач: 1) определить направление проекций перпендикуляра к пл-ти; 2) построить точку пересечения прямой (перпендикуляра) с пл-тью; 3) определить длину перпендикуляра способом прямоугольного треугольника.

 10. Способы преобразования проекций:
Способы преобразования предназначены гл.образом для решения метрических задач, связанных с определением дествит-х размеров и формы изобр-ых на эпюре геометр. объектов.
Основные способы преобразования проекций:
а) способ замены пл-тей проекции
б) способ вращения
в) способ косоугольного вспомогательного проецирования.
Новые проекции точек и осей проекций обозначают теми же буквами, но с цифровым индексом внизу, который опр-т последова-ть преобразований.
Способ косоугольного вспомог.проецирования.
Способы решения задач применяют при решении как метрических, так и позиционных задач. Сущность этого способа закл-ся в применении не прямоугольного, а косоугольного проецирования. Направление проецирование выбирается т.о., чтобы получить вырожденную проекцию объекта, когда прямая проецируется в точку, а пл-ть – в линию. Полученные рез-ты обратным проецированием переносятся на заданные проекции.
Чтобы спроецировать прямую в точку, т.е. получить её вырожденную проекцию, следует выбрать направление проецирования, параллельное прямой (рис.41,а). Вырожденную проекцию пл-ти можно получить, если направление проецирования будет параллельным пл-ти (рис.41,б).
На рису. 41, в задача на пересечение прямой с пл-тью решена вспомогательным косоугольным проецированием на пл-ть Н. Направление проецирования выбрано параллельно стороне АВ тре-ка. Пл-ть тр-ка спроецировалась в прямую а1=d1e1. Обратным преобразованием полученная вспомогательная проекция точки пересенич
прямых MN и KL даст искомую проекцию ар точки A на плоскость Р по заданному направлению проецирования S. Чтобы получить неискаженную косоугольную проекцию, плоскость Р следует совместить с плоскостью чертежа. На рис. 47 все построения выполнены на эпюре. Совмещенное положение следа Ph 0 определено с помощью точки 1. Совмещенное положение прямых MN и KL получено перемещением точек т и k, в которых плоскости Q и Т пересекают след Ph, на совмещенное положение следа Ph 0. Совмещенное положение точки ар находится пересечением совмещенных прямых k 0 l' и m 0 n'. Сущность комбинированного способа и целесообразность его применения могут быть легко выяснены на примере определения точки встречи прямой с плоскостью. Эта задача чрезвычайно распространена, а подчас она является "ключом" при решении более сложных вопросов начертательной геометрии. Обычно при решении этой задачи в системе двух взаимно перпендикулярных плоскостей проекций Н и V мы получим две ортогональные проекции точки встречи прямой с плоскостью. Практически больший смысл представляет зафиксировать положение найденной точки не относительно плоскостей Н и V, а непосредственно на плоскости Р. Комбинированный способ дает возможность получить именно такой ответ.
14.Многогранником называют пространственное тело,поверхность которого образованна пересекающимися многоугольниками.Грань-поверхность ограниченная одним многоугольником.При пересечении граней образуются ребра, они пересекаются в вершинах многограника.
Развертка многог-ка –плоская фигура,образованная разложением всех граней на плоскость одной из них.Разложение производится вращением граней вокруг общих ребер
Б)Построение линии пересечения многограника с заданной плоскостью строится по точкам пересечения ребер сданной плоскостью.ПОСТРОЕНИЕ стр 19-20.глава 2
Построение точек пересечения прямой с поверхностью многограника можно осуществить путем введения вспомогательной секущей плоскости,которая проходит через заданную прямую.Пересечение многогранников плоскостью.Пример конструирования устойчивой подставки в виде усеченной пирамиды показан на рис. 6.4. Наклонная площадка ABCD образована срезом верхней части пирамиды фронтально- проецирующей плоскостью S (S2). Фронтальные проекции a2, b2, c2, d2 точек находятся на фронтальном следе S2 плоскости, а фронтальная проекция площадки ABCD совпадает со следом S2. Профильная a3b3c3d3 и горизонтальная a1b1c1d1проекции площадки построены по проекциям указанных точек на проекциях соответствующих ребер.
пересечение Прямой линии с многогранником
Для определения точек пересечения прямой линии с многогранником, задача сводится к нахождению точек пересечения прямой с
10. Способы преобразования проекций:
Способы преобразования предназначены гл.образом для решения метрических задач, связанных с определением дествит-х размеров и формы изобр-ых на эпюре геометр. объектов.
Основные способы преобразования проекций:
а) способ замены пл-тей проекции
б) способ вращения
в) способ косоугольного вспомогательного проецирования.
Новые проекции точек и осей проекций обозначают теми же буквами, но с цифровым индексом внизу, который опр-т последова-ть преобразований.
Способ косоугольного вспомог.проецирования.
Способы решения задач применяют при решении как метрических, так и позиционных задач. Сущность этого способа закл-ся в применении не прямоугольного, а косоугольного проецирования. Направление проецирование выбирается т.о., чтобы получить вырожденную проекцию объекта, когда прямая проецируется в точку, а пл-ть – в линию. Полученные рез-ты обратным проецированием переносятся на заданные проекции.
Чтобы спроецировать прямую в точку, т.е. получить её вырожденную проекцию, следует выбрать направление проецирования, параллельное прямой (рис.41,а). Вырожденную проекцию пл-ти можно получить, если направление проецирования будет параллельным пл-ти (рис.41,б).
На рису. 41, в задача на пересечение прямой с пл-тью решена вспомогательным косоугольным проецированием на пл-ть Н. Направление проецирования выбрано параллельно стороне АВ тре-ка. Пл-ть тр-ка спроецировалась в прямую а1=d1e1. Обратным преобразованием полученная вспомогательная проекция точки пересенич
прямых MN и KL даст искомую проекцию ар точки A на плоскость Р по заданному направлению проецирования S. Чтобы получить неискаженную косоугольную проекцию, плоскость Р следует совместить с плоскостью чертежа. На рис. 47 все построения выполнены на эпюре. Совмещенное положение следа Ph 0 определено с помощью точки 1. Совмещенное положение прямых MN и KL получено перемещением точек т и k, в которых плоскости Q и Т пересекают след Ph, на совмещенное положение следа Ph 0. Совмещенное положение точки ар находится пересечением совмещенных прямых k 0 l' и m 0 n'. Сущность комбинированного способа и целесообразность его применения могут быть легко выяснены на примере определения точки встречи прямой с плоскостью. Эта задача чрезвычайно распространена, а подчас она является "ключом" при решении более сложных вопросов начертательной геометрии. Обычно при решении этой задачи в системе двух взаимно перпендикулярных плоскостей проекций Н и V мы получим две ортогональные проекции точки встречи прямой с плоскостью. Практически больший смысл представляет зафиксировать положение найденной точки не относительно плоскостей Н и V, а непосредственно на плоскости Р. Комбинированный способ дает возможность получить именно такой ответ.
14.Многогранником называют пространственное тело,поверхность которого образованна пересекающимися многоугольниками.Грань-поверхность ограниченная одним многоугольником.При пересечении граней образуются ребра, они пересекаются в вершинах многограника.
Развертка многог-ка –плоская фигура,образованная разложением всех граней на плоскость одной из них.Разложение производится вращением граней вокруг общих ребер
Б)Построение линии пересечения многограника с заданной плоскостью строится по точкам пересечения ребер сданной плоскостью.ПОСТРОЕНИЕ стр 19-20.глава 2
Построение точек пересечения прямой с поверхностью многограника можно осуществить путем введения вспомогательной секущей плоскости,которая проходит через заданную прямую.Пересечение многогранников плоскостью.Пример конструирования устойчивой подставки в виде усеченной пирамиды показан на рис. 6.4. Наклонная площадка ABCD образована срезом верхней части пирамиды фронтально- проецирующей плоскостью S (S2). Фронтальные проекции a2, b2, c2, d2 точек находятся на фронтальном следе S2 плоскости, а фронтальная проекция площадки ABCD совпадает со следом S2. Профильная a3b3c3d3 и горизонтальная a1b1c1d1проекции площадки построены по проекциям указанных точек на проекциях соответствующих ребер.
пересечение Прямой линии с многогранником
Для определения точек пересечения прямой линии с многогранником, задача сводится к нахождению точек пересечения прямой с  плоскостями граней (рис.78).
Алгоритм решения задачи:
Алгоритм решения задачи:
1. Через заданную прямую mпроводим вспомогательную секущую плоскость (m).
2. Строим сечение многогранника с вспомогательной секущей плоскостью .
3. Определить искомые точки К,М - пересечения полученного сечения с прямой m.
4. Определить видимость прямой по отношению к пирамиде.
плоскостями граней (рис.78).
Алгоритм решения задачи:
Алгоритм решения задачи:
1. Через заданную прямую mпроводим вспомогательную секущую плоскость (m).
2. Строим сечение многогранника с вспомогательной секущей плоскостью .
3. Определить искомые точки К,М - пересечения полученного сечения с прямой m.
4. Определить видимость прямой по отношению к пирамиде.

 б) эпюр
Рисунок 78. Пересечение прямой линии с пирамидой
18..Плоские кривые. Свойства. Проекции плоских кривых. Цепная линия.
Наиболее распространенными являются кривые линии. Для исследования локальных свойств плоской кривой строят в некоторой точке касательную и нормаль.
Касательной к плоской кривой в некоторой её точке называется предельное положение секущей, когда две общие с кривой точки сечения, стремясь друг к другу, совпадут. Касательная определяет направление движения точки по кривой.
Нормалью называется прямая, лежащая в плоскости кривой и перпендикулярная касательной в точке её касательная.
При решении некоторых задач приходится проводить касательную к кривой.
Свойства:
Точка кривой, в которой можно провести единственную касательную, называется гладкой. Кривая, состоящая только из одних гладких точек, называется гладкой кривой. Точка кривой называется обыкновенной, если при движении точки по кривой направление ее движения и направление поворота касательной не изменяются. Точки, не отвечающие этим требованием, называются особыми
Проекции плоских кривых.
Важное значение имеют некоторые кривые второго порядка- эллипс, парабола, гипербола.
Эллипс представляет собой множество точек, сумма расстояний от каждой из которых до двух данных точек (фокусов) есть величина постоянная: |МF1| + |MF2| = 2a.
Окружность– замкнутая плоская кривая, все точки которой одинаково удалены от данной точки (центра). Если R - радиус окружности - расстояние каждой его точки до центра, то длина окружности выразится числом 2pR, а площадь ею ограниченная, числом pR2, где p - отношение длины окружности к её диаметру.
Гипербола представляет собой множество точек, разность расстояния до двух данных точек (фокуса) есть величина постоянная: |МF1| - |MF2| = 2a.
Параболой называется геометрическое место точек, для каждой из которых расстояние до некоторой фиксированной точки плоскости, называемой фокусом, равно расстоянию до некоторой фиксированной прямой, называемой директрисой. Фокус параболы обозначается буквой F, расстояние от фокуса до директрисы - буквой р. Число р называется параметром параболы.
линия пересечения круглого конуса плоскостью, параллельной какой-либо касательной плоскости этого конуса. П. может быть также определена как геометрическое место точек плоскости, для каждой из которых расстояние до определённой точки F плоскости — фокуса П.— равно расстоянию до некоторой прямой MN — директрисы П. Прямая, проходящая через фокус перпендикулярно директрисе и направленная от директрисы к фокусу, называется осью П., а точка пересечения оси с П.— вершиной П.
Величина р называется параметром П. Парабола — линия второго порядка. Если в фокусе П. поместить источник света, то лучи, отразившиеся от П., образуют параллельный пучок, т.к. прямая PF, соединяющая любую точку Р П. с фокусом, и прямая, параллельная оси, образует с нормалью PR равные углы. Это свойство П. применяется, например, для прожекторных устройств.
Цепна́я ли́ния — линия, форму которой принимает гибкая однородная нерастяжимая тяжелая нить или цепь (отсюда название) с закрепленными концами в однородном гравитационном поле. Является плоской трансцендентной кривой
Перевёрнутая цепная линия — идеальная форма для арок. Однородная арка в форме перевёрнутой цепной линии испытывает только деформации сжатия, но не излома.
Горбатый мост имеет форму, близкую к цепной линии.
Стоит заметить, что цепь подвесного моста имеет форму параболы, а не цепной линии. Это связано с тем, что пролёт моста намного тяжелее цепи.
22.Пересечение прямой линии с кривой поверхностью.
Для построения точек пересечения прямой с кривой поверхностью следует через прямую провести
вспомогательную плоскость, найти линию пересечения этой плоскости с поверхностью. Точки пересе-
чения заданной прямой и построенной линии будут искомыми точками пересечения прямой с поверх-
ностью. Вспомогательную плоскость, проводимую через прямую, следует выбирать так, чтобы получа-
лись простые сечения (сечения, которые можно построить с помощью линейки и циркуля).
Пример 1. Построить точки пересечения прямой с поверхностью конуса
б) эпюр
Рисунок 78. Пересечение прямой линии с пирамидой
18..Плоские кривые. Свойства. Проекции плоских кривых. Цепная линия.
Наиболее распространенными являются кривые линии. Для исследования локальных свойств плоской кривой строят в некоторой точке касательную и нормаль.
Касательной к плоской кривой в некоторой её точке называется предельное положение секущей, когда две общие с кривой точки сечения, стремясь друг к другу, совпадут. Касательная определяет направление движения точки по кривой.
Нормалью называется прямая, лежащая в плоскости кривой и перпендикулярная касательной в точке её касательная.
При решении некоторых задач приходится проводить касательную к кривой.
Свойства:
Точка кривой, в которой можно провести единственную касательную, называется гладкой. Кривая, состоящая только из одних гладких точек, называется гладкой кривой. Точка кривой называется обыкновенной, если при движении точки по кривой направление ее движения и направление поворота касательной не изменяются. Точки, не отвечающие этим требованием, называются особыми
Проекции плоских кривых.
Важное значение имеют некоторые кривые второго порядка- эллипс, парабола, гипербола.
Эллипс представляет собой множество точек, сумма расстояний от каждой из которых до двух данных точек (фокусов) есть величина постоянная: |МF1| + |MF2| = 2a.
Окружность– замкнутая плоская кривая, все точки которой одинаково удалены от данной точки (центра). Если R - радиус окружности - расстояние каждой его точки до центра, то длина окружности выразится числом 2pR, а площадь ею ограниченная, числом pR2, где p - отношение длины окружности к её диаметру.
Гипербола представляет собой множество точек, разность расстояния до двух данных точек (фокуса) есть величина постоянная: |МF1| - |MF2| = 2a.
Параболой называется геометрическое место точек, для каждой из которых расстояние до некоторой фиксированной точки плоскости, называемой фокусом, равно расстоянию до некоторой фиксированной прямой, называемой директрисой. Фокус параболы обозначается буквой F, расстояние от фокуса до директрисы - буквой р. Число р называется параметром параболы.
линия пересечения круглого конуса плоскостью, параллельной какой-либо касательной плоскости этого конуса. П. может быть также определена как геометрическое место точек плоскости, для каждой из которых расстояние до определённой точки F плоскости — фокуса П.— равно расстоянию до некоторой прямой MN — директрисы П. Прямая, проходящая через фокус перпендикулярно директрисе и направленная от директрисы к фокусу, называется осью П., а точка пересечения оси с П.— вершиной П.
Величина р называется параметром П. Парабола — линия второго порядка. Если в фокусе П. поместить источник света, то лучи, отразившиеся от П., образуют параллельный пучок, т.к. прямая PF, соединяющая любую точку Р П. с фокусом, и прямая, параллельная оси, образует с нормалью PR равные углы. Это свойство П. применяется, например, для прожекторных устройств.
Цепна́я ли́ния — линия, форму которой принимает гибкая однородная нерастяжимая тяжелая нить или цепь (отсюда название) с закрепленными концами в однородном гравитационном поле. Является плоской трансцендентной кривой
Перевёрнутая цепная линия — идеальная форма для арок. Однородная арка в форме перевёрнутой цепной линии испытывает только деформации сжатия, но не излома.
Горбатый мост имеет форму, близкую к цепной линии.
Стоит заметить, что цепь подвесного моста имеет форму параболы, а не цепной линии. Это связано с тем, что пролёт моста намного тяжелее цепи.
22.Пересечение прямой линии с кривой поверхностью.
Для построения точек пересечения прямой с кривой поверхностью следует через прямую провести
вспомогательную плоскость, найти линию пересечения этой плоскости с поверхностью. Точки пересе-
чения заданной прямой и построенной линии будут искомыми точками пересечения прямой с поверх-
ностью. Вспомогательную плоскость, проводимую через прямую, следует выбирать так, чтобы получа-
лись простые сечения (сечения, которые можно построить с помощью линейки и циркуля).
Пример 1. Построить точки пересечения прямой с поверхностью конуса

 Пример 2. Построить точки пересечения прямой с поверхностью сферы
Пример 2. Построить точки пересечения прямой с поверхностью сферы
 26.Плоские кривые. Свойства проекции плоских кривых. Цепная линия.
П л о с к и е к р и в ы е
Плоские кривые имеют касательную, нормаль и кривизну.
Касательной называется предельное положение секущей, когда две общие с кривой точки стремятся друг к другу и совпадут в одной точке. Касательная – это прямая, имеющая общую точку с кривой. Нормалью называется прямая, лежащая в плоскости кривой и перпендикулярная касательной в точке ее касания. Кривизной плоской кривой в данной точке называется величина, обратная радиусу соприкасающейся окружности (r) Основные виды плоской кривой: окружност
26.Плоские кривые. Свойства проекции плоских кривых. Цепная линия.
П л о с к и е к р и в ы е
Плоские кривые имеют касательную, нормаль и кривизну.
Касательной называется предельное положение секущей, когда две общие с кривой точки стремятся друг к другу и совпадут в одной точке. Касательная – это прямая, имеющая общую точку с кривой. Нормалью называется прямая, лежащая в плоскости кривой и перпендикулярная касательной в точке ее касания. Кривизной плоской кривой в данной точке называется величина, обратная радиусу соприкасающейся окружности (r) Основные виды плоской кривой: окружност