Поверхности второго порядка
Уравнения вида
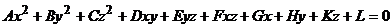 ,
,
где по крайней мере один из коэффициентов A, B, C, D, E, F отличен от нуля, называется уравнением второго порядка. Уравнение второго порядка в декартовых координатах определяет поверхность второго порядка.
Для каждого уравнения второго порядка можно указать такую систему координат, в которой это уравнение примет наиболее простой вид
 ,
,
Затем, используя стандартную операцию выделения полных квадратов, уравнение приводится к каноническому виду. Существует всего семь типов канонических уравнений поверхностей второго порядка:
1. уравнение эллипсоида: 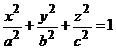 ,
,
2. уравнение однополостного гиперболоида:  ,
,
3. уравнение двуполостного гиперболоида:  ,
,
4. уравнение конуса второго порядка:  ,
,
5. уравнение эллиптического параболоида:  ,
,
6. уравнение гиперболического гиперболоида:  ,
,
7. цилиндрические поверхности:
а) эллиптический цилиндр:  ,
,
б) гиперболический цилиндр:  ,
,
в) параболический цилиндр: 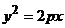 .
.
Эллипсоид.
Исследуем форму эллипсоида по его каноническому уравнению:
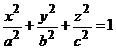 .
.
Координатные плоскости являются плоскостями симметрии, а начало координат – центром симметрии эллипсоида.Числа a, b и c называются полуосями эллипсоида. Точки пересечения эллипсоида с координатными осями имеют координаты (а, 0, 0), (-a, 0, 0), (0, b, 0), (0, -b, 0), (0, 0, c), (0, 0, -c).
Чтобы представить себе форму эллипсоида, воспользуемся методом «параллельных сечений». Будем рассматривать сечения поверхности плоскостями z = h, параллельными плоскости Оху. В сечении получим эллипсы 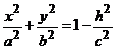 ,
,
если | h | < c. Если h = ± c, то в сечении будет точка, а если | h | > c, то плоскость z = h и эллипсоид пересекаться не будут. Отметим еще, что при h = 0 в сечении будет самый большой эллипс, а при возрастании h эллипс в сечении уменьшается.
Аналогичная картина получается, если рассматривать сечения эллипсоида плоскостями x = h и у = h.
Таким образом, эллипсоид есть замкнутая овальная поверхность (рис. 3.31).
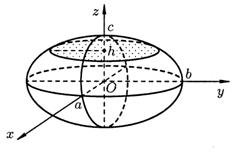
Рисунок 3.31
Если a = b = c = R, то эллипсоид является сферой радиуса R:  .
.
Уравнение вида  , называется уравнением мнимого эллипсоида.
, называется уравнением мнимого эллипсоида.
Однополостный гиперболоид.
Рассмотрим каноническое уравнение однополостного гиперболоида:  .
.
Координатные плоскости являются плоскостями симметрии однополостного гиперболоида, а начало координат – его центром симметрии.
Нетрудно определить точки пересечения гиперболоида с координатными осями: (а, 0, 0), (-a, 0, 0), (0, b, 0), (0, -b, 0). С осью Oz однополостный гиперболоид не имеет точек пересечения. Рассмотрим сечения однополостного гиперболоида плоскостями z = h. При любом h в сечении получим эллипсы:  .
.
Причем при h = 0 в сечении будет самый маленький эллипс с полуосями а и b. А при возрастании | h| эллипсы будут увеличиваться.
Рассмотрим сечения поверхности гиперболоида координатными плоскостями Охz и Oyz. Эти плоскости определяются уравнениями y = 0 и х = 0, соответственно. Поэтому сечения будут определяться уравнениями: 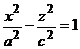 и
и  .
.
Это есть уравнения гипербол.
Таким образом, однополостный гиперболоид имеет вид бесконечной трубки, расположенной вдоль оси Oz и расширяющейся как в положительном, так и в отрицательном направлении (рис. 3.32).

Рисунок 3.32
Заметим, что если а = b, то в сечении гиперболоида плоскостью z = h будет окружность. Тогда однополостный гиперболоид можно рассматривать как поверхность, образованную вращением гиперболы вокруг одной из ее осей симметрии (той, которая ее не пересекает).