Рассмотрим каноническое уравнение гиперболического параболоида: 
.
Из этого уравнения следует, что координатные плоскости Oxz и Oyz являются его плоскостями симметрии, а ось Oz – его осью симметрии.
Рассмотрим сечения гиперболического параболоида плоскостями z = h. Они определяются уравнениями
,
и представляют собой гиперболы, пересекающие ось Ох, при h > 0. При h <0 в сечении будут сопряженные гиперболы, пересекающие ось Оу, а при h = 0 в сечении получатся прямые 
. Т.е. гиперболический параболоид пересекает координатную плоскость Оху по двум пересекающимся прямым.
Сечения плоскостями x =h определяются уравнениями 
, и представляют собой нисходящие вдоль оси Oz параболы. При h = 0 вершина параболы будет находиться в начале координат.
Сечения плоскостями у = h также представляют собой параболы 
,
но уже восходящие вдоль оси Oz. При h = 0 вершина снова будет находиться в начале координат.
Таким образом, гиперболический параболоид имеет форму седла, установленного на оси Ох (рис. 3.35).
Уравнение вида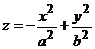 
также определяет гиперболический параболоид, но расположенный уже вдоль оси Оу.
Рисунок 3.35
Конус второго порядка.
Конус второго порядка определяется уравнением 
.
Все координатные плоскости являются плоскостями симметрии конуса.
Заметим, что поверхность конуса обладает следующим свойством: если некоторая точка М лежит на поверхности конуса, то и любая другая точка М¢ лежащая на прямой, соединяющей М с началом координат, также лежит на этом конусе.
В самом деле, если точка М имеет координаты 
, то точка М¢ должна иметь координаты 
для некоторого t. Подставим координаты точки М¢ в уравнение конуса: 
, Тогда 
.
Получили верное равенство, так как по предположению точка М лежит на поверхности конуса. Следовательно, точка М¢¢ также лежит на поверхности конуса.
Из доказанного свойства следует, что поверхность конуса образована прямыми, проходящими через начало координат (рис. 3.36).
Сечения поверхности плоскостями z = h определяются уравнениями 
,
и представляют собой эллипсы при h ¹ 0. Если h = 0, то в сечении будет одна точка – начало координат.
Если а = b, то в сечении плоскостями z = h будут окружности. Такой конус называется круглым.
Рисунок 3.36
Цилиндры второго порядка.
Уравнение поверхности, не содержащее одной из координат, определяет цилиндрическую поверхность.
Например, если уравнение поверхности не содержит координаты z, то оно определяет цилиндрическую поверхность с образующими, параллельными оси Оz.
Цилиндром второго порядка с образующими, параллельными оси Оz, называется поверхность, определяемая уравнением 2-й степени, не содержащим координаты z.
Существует три типа цилиндров второго порядка:
а) эллиптический цилиндр: 
,
б) гиперболический цилиндр: 
,
в) параболический цилиндр: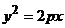 
.
На рис. 3.37 изображены поверхности эллиптического, гиперболического и параболического цилиндров.
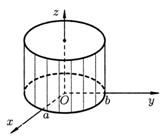
а) б) в)
Рисунок 3.37