RESOLUTIONOFKINEMATICREDUNDANCY
J. Baillieul, D.P. Martin
1990
РАЗРЕШЕНИЕ КИНЕМАТИЧЕСКОЙ ИЗБЫТОЧНОСТИ
Аннотация
Кинематически избыточные роботизированные механизмы имеют больше степеней свободы, чем минимально требуется для выполнения заданного класса задач. Эта статья посвящена кинематической избыточности в манипуляторах и описывает недавние исследования по планированию движения для таких устройств. Краткая история проблемы обратной кинематики для избыточных манипуляторов начинается с обсуждения ограничений, недавно обнаруженных с помощью псевдо-обратных методов. В частности, показывается, что такие методы неизбежно сталкиваются с кинематическими особенностями и не являются «повторяемыми ». Будет определён и обсуждён метод расширенного Якобиана, по сути, это единственныйлокальный метод с повторяемыми движениями для задачи генерациипутейв пространстве сочленений. Также отмечается, что любой метод (например, метод расширенного Якобиана), который разрешает кинематическую избыточность посредством кинематических ограничений на движения в пространстве сочленений, неизбежно включает алгоритмические особенности. Последствия таких особенностей для локальных методов планирования также будут обсуждены далее. Кроме того, представлены вычислительные методы для оптимального разрешения кинематической избыточности. В терминах краевых задач даются необходимые условия оптимальности по траекториям, и на примерах показывается, что истинное оптимальное решение должно выбираться из семейства взаимно неоднородных (nonhomotopic) локально оптимальных решений. Будет показано, как гомотопическое продолжение (homotopycontinuation) может использоваться как для упрощения вычислений, которые в противном случаепотребовали бы значительных вычислительных ресурсов, так и для выделения глобально оптимальных траекторий пространства сочленений среди (бесконечного) множества локально оптимальных кандидатов, удовлетворяющих основным необходимым условиям.
Введение
В этой главе даётся краткое описание современного состояния исследований в области кинематически избыточных манипуляторов. Хотя по соображениям времени и пространства статьимы вынуждены быть избирательными в акцентах на различные темы, и постарались выделить ряд наиболее важных материалов, появившихся за последние 5 лет. Обсуждение организовано следующим образом: Раздел 1 описывает математическое окружение и ставитпринципиальные математические задачи, связанные с планированием движения для кинематически избыточных манипуляторов. В конце раздела обсудим важные различия между локальными и глобальными методами разрешения кинематической избыточности. Раздел 2 освещает некоторые прошлые работы по этим задачам и обсуждает недавно обнаруженные недостатки в когда-то широко изученных обобщённых методах обратной кинематики. Локальные методы разрешения кинематической избыточности с повторяемостью включают функциональные ограничения на переменные сочленений, в Разделе 3 вводим технику расширенного Якобиана для реализации и анализа функционально ограниченных движений. В Разделе 4 обсуждаются глобальные методы и наблюдется то, что оптимизация по траекториям приводит к необходимым условиям, заданным в терминах краевых задач. Хотя решения таких задач могут повлечь за собой значительную вычислительную нагрузку, мы опишем вычислительный подход, основанный на продолжении гомотопии (homotopycontinuation), который, как показал недавний опыт, довольно хорошо работает для выбранных задач. Теоретическое обоснование этих методов в настоящее время не завершено, и глава завершается результатами возмущенныхособенностями необходимых условий (singularlyperturbednecessaryconditions), возникающих при определении гомотопии [1] между вычислительно сложным глобальным методом (приведенным в терминах ОДУ[2] второго порядка) и менее вычислительно сложным локальным методом (где необходимые условия могут быть описаны чисто алгебраическими уравнениями).
Кинематическая избыточность встречается в робототехнике всякий раз, когда устройство или механизм имеет больше степеней свободы, чем необходимо для выполнения предписанной задачи. Таким образом, кинематическая избыточность будет характерна для рук со множеством пальцев, манипуляторов на мобильных платформах, систем из нескольких манипуляторов с общим рабочим пространством и манипуляторов, у которых число степеней свободы сочленений превышает минимально необходимое для выполнения данной задачи или класса задач. Большинство вопросов и результатов этой статьи в равной степени относятся ко всем этим случаям кинематической избыточности. Точное изложение результатов требует внимания к качественным механическим различиям в системах, однако, чтобы избежать чрезмерно сложных и сильно расплывчатых формулировок результатов, мы будем только рассматривать явнуюкинематическую избыточность в манипуляторах. С небольшой потерей общности также предположим, что рассматриваемые манипуляторы представляют собой единые открытые кинематические цепи только с низшими кинематическими парами (lowerpairjoints[3]). Напомним, что низшие пары сочленений соединяют пары соседних звеньев, позволяя относительные движения, которые идеализируются как скольжение без трения по парам контактных поверхностей. Низшие пары исторически играли важную роль в теории и разработке механизмов, а в последнее времяотносительные движения твёрдого тела, которые они определяют, характеризуются в терминах некоторых выделенных подгрупп SE(3,R) [4], группы движений при жёстких связях (rigidmotion) в трёхмерном пространстве. Следуя [15], сделаем следующее определение.
Определение 1.1. Подгруппу G в SE(3,R) назовём подгруппой сочленения, если в SE(3,R) есть окрестность U нейтрального элемента (identity) и пара соприкасающихся твёрдых тел, таких что внутри U множество всех относительных конфигурацийэтих тел идентично G.
6 типов низших кинетических пар суставов определяются следующим образом:
Предложение 1.1 (Loncaric, [15]) Единственными типами подгрупп сочленений являются:
· T(l) (призматическое) (=множество всех перемещений в определенном направлении),
· SO(2) (вращательное) (=множество вращений вокруг данной оси),
· SO(2)p (винтовое) (=группа движений винта с шагом p вокруг заданной оси),
· SO(2) × T(l) (циллиндрическое), SE(2,H) (плоское) и SO(3) [5] (сферическое) (=набор правильных вращений в 3D).
В области кинематики роботов изучается взаимосвязь между конфигурациями пространства сочленений (jointspace) и конфигурациямиоперационного (рабочего) пространства (operationalspace=workspace). Для изучаемых манипуляторов с открытой цепью рабочее пространство просто относится к пространству возможных положений и ориентаций концевой плоскости, концевого эффектора, инструмента или наконечника-захвата(далее захвата). Пространство конфигураций сочленений M (или просто пространство сочленений) будет произведением M = G1 × … × Gk подгруппсочлененийс унаследованной различной структурой. Для настоящих манипуляторов пространствосочленений, как правило, будет строгим подмножеством такой группы-произведения из-за неизбежных суставных ограничений, которые ограничивают диапазон движений. Операционное пространство X также может быть смоделировано как подмножество произведений подгрупп сочленений, и поскольку рассматриваются механизмы с открытой кинематической цепью, каждой конфигурации сочленений θ∈M будет соответствовать уникальная конфигурация рабочего пространства x∈X. Обозначим это функциональное отношение, написав:
x = f (θ). (1)
| Y | y |
На этом уровне абстракции задача обратной кинематики состоит в том, чтобы решить уравнение (1) или, в более общем смысле, найти правый обратный для f. Поскольку f, как правило, является неоднозначной (many-to-one) нелинейной функцией, решение для (1) может бытьсложным и включать определенные варианты. Однако теория представлений SE(3,R) поддерживает явные вычисления. Стандартный подход к представлению кинематики роботов, который неявно использует эту теорию, развился из работ Денавитаи Хартенберга([9]). Более поздняя работа Брокетта[6], с другой стороны, непосредственно использует структуру группы Ли SE(3,R), чтобы выразить кинематические отношения через произведенияматричных экспонент [7]. В любом из этих подходов координатная система прикреплена к каждому звену кинематической цепи. Затем можно представить положение и ориентацию каждой из этих систем координат относительно её предшественника с помощью матрицы 4×4
(«однородного преобразования, homogeneoustransformation),
Здесь Y – ортогональная матрица [8] 3×3, задающая ориентацию, у – 3-столбец, задающий координаты начала системы отсчёта относительно предыдущей системы отсчёта в цепи. Детали формализма Денавита-Хартенберга можно найти во многих стандартных текстах по робототехнике (например, [8]), а элегантный подход Брокеттаописан в первой главе этой книги.
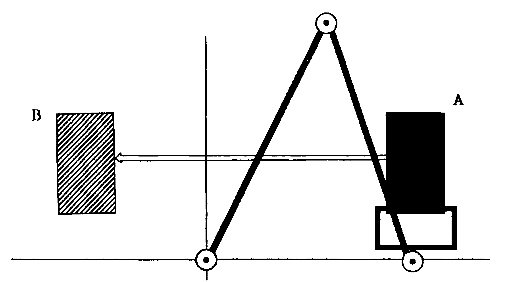
Рисунок 1: Плоский манипулятор с тремя вращающимися сочленениями
Рациональный подход к задаче обратной кинематики для связывания конфигурации сочленения θ с заданной конфигурацией рабочего пространства заключается в поиске того значения θ, которое оптимизирует некоторую целевую функцию g(θ) при условии соблюдения ограничения f(θ)=x. При разумных предположениях математика, лежащая в основе такой поточечной оптимизации, не должна включать в себя ничего большего, чем многовариантное исчисление (multivariablecalculus). Если, как это обычно бывает в приложенияхробототехники, путь указан в конфигурациях рабочего пространства x(t), то не всегда просто создать соответствующий путь θ(t), и сопутствующие математические вопросы будут обсуждаться в оставшейся части этой статьи.
Примеры кинематической избыточности и механизмов с симметриями задач
Поскольку операционное пространство X любого робота является подмножеством произведения подгрупп сочленений в SE(3,R), удобно обсуждать вычислительные вопросы, возникающие из симметрии задач прямой и обратной кинематики, с точки зрения действий в группах.
Если X=G1 × … × Gk, где каждый Gj является подгруппой в SE(3,R), то естественное левое действие G × XàX задаётся, как g*(g1, …., gk)=(gg1,..., ggk), а правое действие X × GàX даётся выражением
(g1,..., gk)*g=(g1g,..., gkg). Пусть G⊂SE(3,R) – подгруппа. Мы говорим, что существует (левая)
G -эквивалентность между конфигурациями операционного пространства x1,x2∈X, если существует такое g∈G, что x2= gx1. При этом определении не оговорено, что G является подгруппой сочленения, и, как будет показано в следующих примерах, иногда интересно изучать G - эквивалентность относительно конечных подгрупп в SE(3,R).
Пример 1.1. Пространство суставов плоского манипулятора, изображенного на рис.1, равняется T3=S1 × S1 × S1, где каждая суставная координата θ∈S1 обозначает относительный угол между соответствующими последовательными звеньями. Набор конфигураций рабочего пространства представляет собой набор всех возможных положений и ориентацийзахвата (или кисти руки) относительно некоторой выделенной базовой системы координат. На Рисунке 1 начало базовой системы отсчёта совпадает с 1м соединением, а операционное пространство можно представить, как:
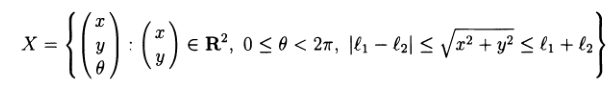
Функциональная связь (1) между пространством сочленений и оперативным пространством принимает вид:
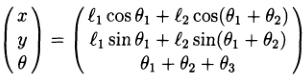(2)
Чтобы подчеркнуть представление X как подгруппы сочленения, также можно записать операционное пространство X в терминах стандартного матричного представления 3×3 (однородное преобразование) SE(2,R):
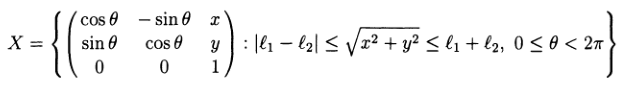
Помимо некоторых особых конфигураций (которые опишем позже), существуют 2 различные конфигурации пространства суставов (отвод локтя вверх и вниз), соответствующие через (2) каждой точке рабочего пространства.
Пример 1.2 Если добавитьзвено и сочленениеманипулятору, описанному в Примере 1.1, получим механизм, рабочее пространство которого остаётся круглой областью на плоскости, пространство сочленений равно M = T4 = S1 × S1 × S1 × S1. (см. Рисунок 5 ниже).
Обратите внимание, что dimM>dimX.
Поскольку имеется больше степеней свободы пространства сочленений, чем минимально необходимое (= 3 в этом случае) для произвольного позиционирования и ориентации кисти манипулятора в рабочем пространстве, механизм, описанный в Примере 1.2, называется кинематически избыточным.
Следующие примеры приведут к более общему определению кинематической избыточности.Многие вопросы планирования движения для кинематически избыточных механизмов, присутствуют в планировании движения при наличии симметрии задачи.
Пример 1.3. Предположим, что плоскому манипулятору, изображенному на Рисунке 1, дана задача вставитьдеталь в виде правильного треугольника с углами 30° и 60° в отверстие той же геометрии (см. Рисунок 2). Манипулятор должен соотнести положение и ориентацию детали относительно отверстия,поскольку для этого есть только 1 способ, существует ровно 2 конфигурации пространства сочленений (локоть вверх или вниз), которые приведут ксовпадению детали сотверстием.
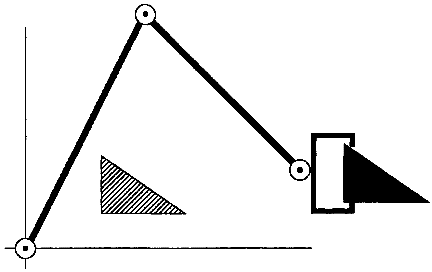
Рисунок 2: Плоский манипулятор, вставляющий треугольную деталь
в отверстие аналогичной формы
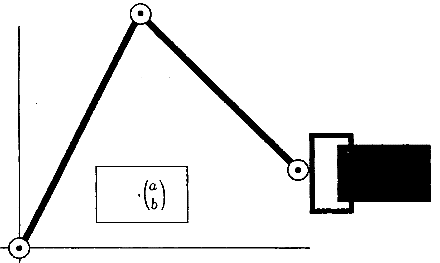
Рисунок 3: Плоский манипулятор, вставляющий прямоугольную деталь
в отверстие аналогичной формы
Пример 1.4. Предположим, что на следующем этапе плоскому манипулятору дана задача вставить прямоугольную деталь или заготовку в прямоугольное отверстие (см. Рисунок 3). Предположим, что центр прямоугольника имеет координаты (a,b)Т относительно базовой системы отсчёта манипулятора. Предполагая, что захват с координатами (x,y,θ)Т расположен и ориентирован, как
(x,y,θ)Т = (2a-x, 2b-y, θ+π)Т
тодеталь также совпадёт с отверстием. Таким образом, существует 4 конфигурации пространства сочленений, соответствующие детали, выровненной по отверстию.
Пример 1.5. В предыдущем примере, предположим, что задача модифицирована для вставки круглого «колышка » (peg) радиуса r в круглое отверстие также с радиусом r и центром в (a,b)Т. Колышек в захвате совпадёт с отверстием при конфигурации,заданнойдлялюбого φ
(x,y,θ)Т = ((a — rcosφ), (b — rsinφ), φ)Т
Очевидные симметрии 2х предыдущих примеров могут быть формально описаны в терминах
G- эквивалентности в операционном пространстве. Это очевидно, если смотреть из локальной системы отсчёта, начало которой находится в (a,b)Т (= центр отверстия).
Вданной локальной системе отсчёта симметрия задачи из Примера 1.4 описывается
G- эквивалентностью в операционном пространстве, где G является подгруппой в SE(2,R), которая изоморфна Z2 и порождена поворотом на 180°:
Локальная G- эквивалентность Примера 1.5 задается формулой:
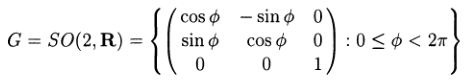
Если операционное пространство описано относительно базовой системы отсчёта, а не локальной, группы симметрии этих примеров получаются связыванием [9] (conjugation). Для Примера 1.4
G генерируется элементом
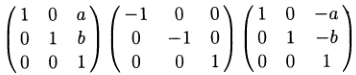
Тогда для Примера 1.5 группа G является связанной с S0(2) для 0≤φ≤2π
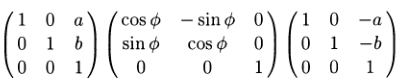
Мы отмечаем в обоих этих примерах, что если
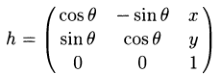
определяет положение и ориентацию захвата, для которого деталь совпадает с отверстием, то любая конфигурация gh c g∈G также определяет положение/ориентацию детали, которая совпадает с отверстием.
Симметрии задачи типов, показанных в этих примерах, встречаются во многих приложениях роботов. Например, при сварке (welding) любое вращение сварочной горелки (weldingtorch) вокруг её продольной оси не имеет значения, и эта симметрия задачи эффективно уменьшает размер рабочего пространства. (Сварочные роботы часто на самом деле имеют 5, а не 6 степеней свободы именно для того, чтобы воспользоваться этой симметрией задачи). В более общем смысле можно обнаружить, что, когда задача допускает G- эквивалентность,вопрос позиционирования и ориентации захвата в операционном пространстве X может быть упрощён всякий раз, когда нет необходимости проводить различие между G- эквивалентнымиконфигурациями (различия между G- эквивалентнымиконфигурациями будут важны в приложениях, где невозможно достичь всех
G- эквивалентных конфигураций манипулятора, например, где рабочее пространствоперегорожено). Когда такие различия несущественны, можно упростить анализ путём формальногоотождествления G- эквивалентных конфигураций. Важный случай возникает, когда орбиты G (orbitsof G)[10]охватывают регулярноеслоение (regularfoliation)[11] X. За исключением некоторых особенностей (singularities), X будет в широком множестве интересных случаев слоиться (foliate) на G - орбиты. В этом случае X=X/G имеет естественно дифференцируемую структуру и кинематическое отображение f:MàX определяет дифференцируемое отображение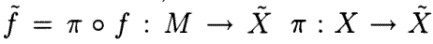 
, где π - естественная проекция [12]. Х` называется сокращенным оперативным пространством. Обратите внимание, что dimX`≤dimX, и неравенство строгое при dimG>0. Теперь можно сформулировать следующее формальное определение.
Определение 1.2. Пусть дан робот-манипулятор с пространством сочленений M, (сокращенным) рабочим пространством X и (сокращенным) кинематическим отображением f:MàX. Если dimM>dimX, то говорим, что манипулятор кинематически избыточен.
Это определение расширяет класс кинематически избыточных манипуляторов для включения механизмов, для которых избыточность является чистым артефактом симметрии в задаче, которой они предназначены. Когда группа симметрии задачи имеет размерность 0, как в Примере 1.4, манипулятор не является кинематически избыточным в формальном смысле. Тем не менее, диапазон выбора при решении обратной задачи кинематики увеличивается при любой симметриизадачи, и, как мы заметим ниже, механизмы с симметрией задачи представляют некоторые из тех же проблем при планировании пути, что и кинематически избыточные манипуляторы.
Проблемы в Планировании Движения.
Основная проблема, рассматриваемая в этой статье, заключается в поиске траектории в пространстве сочленений θ(•), которая путём (1) соответствует заданной траектории в оперативномпространстве x(•). Простые примеры, которые мы привели, иллюстрируют ключевое свойство планирования движения в пространстве сочленений, общее для избыточных и неизбыточных манипуляторов: существует (возможно, бесконечно) много путей в пространстве сочленений, соответствующих каждому пути в оперативномпространстве. Критерии выбора путей:
· Траектория сочленений θ(t) должна описывать замкнутую кривую всякий раз, когда соответствующая траекториязахвата x(t) описывает замкнутую кривую.
· Траектории суставов должны быть как можно более плавными (в реальном роботе грубые и резкие движения могут повредить механизм), и общее движение суставов должно быть не больше, чем необходимо для получения заданного движения захвата.
· Механические соображения ограничивают возможные движения любого манипулятора. Хотя мы отождествляем движения низших пар с суставными подгруппами, как правило, движениябудут ограничены некоторым подмножеством конфигураций, определённых группой, поскольку расстояние перемещения в любом суставе на практике будет ограничено, и механизм не может быть сделан так, чтобы его твёрдые элементымогли проходить сквозьдруг друга. Таким образом, мы принимаем эмпирическое правило о том, чтоследует избегатьограничения суставов с максимально возможным запасом при любой траектории пространства сочленений.
· Конфигурации в пространстве сочленений, при которых Якобиан J=∂f/∂θ снедостаточным рангом называются кинематические особенности. Как мы заметим ниже, когда конфигурация манипулятора близка к кинематической особенности, для умеренных скоростей захвата требуются очень большие скорости соединений. Таким образом, нужно определять траектории для сочленений, избегающие с достаточным запасом особенности.
· Поскольку при определении движений кинематически избыточного механизма необходимо сделать выбор, этот выбор должен оптимизировать некоторые рациональные цели. В предыдущих трёх пунктах подразумеваются кинематические критерии оптимальности. Другие критерии могут быть определены с точки зрения динамических соображений (минимальное ускорение, минимальная требуемая мощность приводов и т.д.).
Замечание о кинематических особенностях требует некоторого усиления (amplification). Дифференцируя соотношение (1), получаем уравнение скорости:
x˙ = J θ˙ (3)
где J – Якобиан от f. Если J имеет неполный ранг (т.е. механизм находится в кинематически особенной конфигурации), существуют значения x˙, для которых θ˙ не удовлетворяет (3). На практике можно обнаружить, что вблизи конфигураций с кинематическими особенностями умеренные значения || x˙ || требуют очень больших значений || θ˙ ||, чтобы удовлетворить (3). Для неизбыточныхманипуляторов кинематические особенности вообще неизбежны. Пример 1.1 иллюстрирует это тем, что любая конфигурация, для которой sin θ2 = 0, является особенностью. Таким образом, если L1=L2, приведение позиции захвата в положение,точно совпадающеес базой,вводит механизм в конфигурацию особенности. В Пример 1.2 особенностью является любая конфигурация, где sinθ2=sinθ3=0. Это иллюстрирует важный момент: добавление большего количества степеней свободы к механизму не исключает возможности особенных конфигураций.
Независимо от того, является ли манипулятор кинематически избыточным в выборе траекторий пространства сочленений, будем руководствоваться задачами, которые выделили. В связи с этим рассмотрим два различных подхода к разрешению кинематической избыточности.
Локальные методы решают (3) для θ˙ в терминах θ и x в каждый момент времени, а затем генерируют весь путь в пространстве суставов, интегрируя θ˙.
Глобальные методы, с другой стороны, стремятся определить сразу весь путь θ (•) в терминах всего путив оперативном пространстве х(•).
Поскольку глобальные методы используют весь путь в оперативном пространстве, они необязательно выряжают явную связь (noncausal),поэтому не очень подходят для алгоритмов реального времени. Локальные методы, напротив, используют только текущую информацию для определения следующего шага в планировании движения суставов. В принципе, они способны адаптироваться к непредвиденным изменениям в пути в оперативном пространстве, могут использоваться в алгоритмах планирования, которые применяют данные с датчиков в реальном времени. Более того, как отметим ниже, их реализация предъявляет меньше пугающих вычислительных требований, чем глобальные методы. Основным недостатком локальных методов является неизбежность появления алгоритмических особенностей (см. Раздел 3).Такой подход к планированию, в разумном смысле оптимальный в каждый момент времени, не способен включать информацию о будущих последствиях текущих движений, представляет предельнуюпотерю производительности. Локальные методы будут обсуждаться в следующих двух разделах, в то время как глобальные методы будут рассматриваться в Разделе 4.
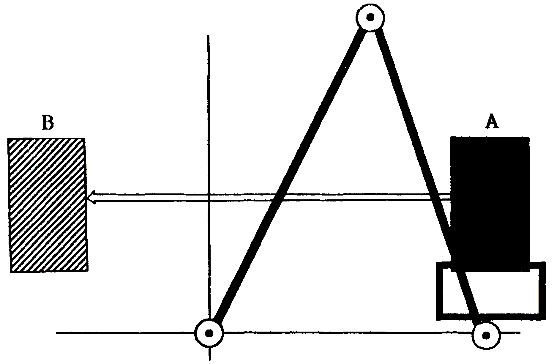
Рисунок 4: Задача манипулятора – переместить детальиз А в В по указанному пути
Пример 1.6. Рассмотрим механизм и обрабатываемую деталь, описанные в Примере 1.4. Предположим, что мы хотим переместить детальиз положения A в положение B вдоль рабочего пространства, как показано на Рисунке 4, держа её сверху или снизу. Если обрабатываемая деталь захвачена снизу, то от манипулятора требуется значительно меньше общего движения, чем для захваченной сверху.Поскольку от первого соединения в движении захвата снизу требуется существенно меньшее движение. Если x -координаты A,B равны соответственно e и -e, относительная разница в движениях, необходимых для захвата снизу и сверху, становится более выраженной, когда eà 0. Локальные методы слепы к таким различиям.