Практическая привлекательность кинематически избыточных роботов-манипуляторов заключается в их повышенном потенциале для работы в насыщенной объектами среде (congestedenvironment) и в возможности избегать оперирования вблизи пределов сочленений или кинематически особенных конфигураций. Напомним из последнего раздела, что, если L1=L2 в Примере 1.1, то размещение захвата у основания манипулятораприводитего в особенную конфигурацию. Кинематически избыточный манипулятор из Примера 1.2 имел кинематические особенности кроме тех, чтосоответствуют расположению захвата на границе операционного пространства, которых можно избежать: всякий раз, когда механизм находится в особенной конфигурации, он может быть перенастроен с помощью «самодвижения » (self-motion)– движения, что оставляет захват неподвижным, а перемещает суставы в конфигурацию без особенности. В этом примере ставится два вопроса:
1. возможно ли добавить дополнительную степень свободы в пространство суставов, чтобы создать механизм робота без особенностей,
2. существует ли математическая характеристика, помогающая различать избегаемые и неизбежные кинематические особенности?
Частичный ответ на второй вопрос был недавно дан Shamir[22], который использует качественную теорию дифференциальных уравнений для классификации особенностей избыточных манипуляторов с 3мя суставами.
На первый вопрос был данответдля случая манипуляторов с кинематическими парами вращения с одной степенью свободыHollerbach[11] с помощью физического аргументаи Gottlieb[10] с помощью топологического аргумента. Следующая теорема была 1м результатом по этому вопросу.
Теорема 2.1 (Брокетт, [6]). Любой робот-манипулятор, чьи соединения имеют тип SO(2) (=одна степень свободы вращения), будет иметь кинематически особенности.
Доказательство: в контексте плоских механизмов наши замечания относительно Примера 1.2 могут быть просто расширены на общий случай. Для пространственных механизмов формула
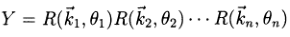(4)
даёт стандартное описание Брокеттаили Денавита-Хартенберга ориентации захвата Y с точки зрения углов суставов θj. Здесь R(k,θ) обозначает собственно ортогональную матрицу [13] 3×3, соответствующую повороту θ, в направлении против часовой стрелки относительно оси, определенной единичным вектором k.
Утверждаем, что для любых 3х последовательных сомножителей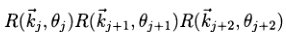 
в этом выражении существует выбор θj+1 такой, что ось kj лежит в плоскости, определяемой kj+1 и kj+2. Предположим, что системы координат были выбраны таким образом, что kj представляет собой (x1,x2,x3)T в j - й системе координат цепи, а kj+1 и kj+2 – соответственно, (0,0,1)T и (y1,y2,y3)T в j+1 - й системе координат. Тогда R(kj+1, θj+1) представляется матрицей
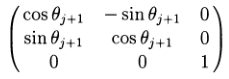
относительно j+1 - й системыкоординат, а единичный вектор kj есть
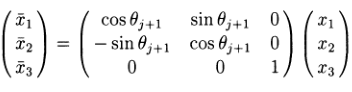
относительно этой системы. Ясно, что либо (x1,x2,x3)T = (0,0,1)T, либо есть некоторый другой выбор θj+1 такой, что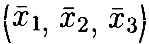 
T лежит в плоскости, определённой (0,0,1)T и (y1,y2,y3)T, в любом случае доказывая наше утверждение.
Установив данное утверждение, далее следует, что для j=2,...,n-1, углы сочленений θj могут быть выбраны так, что все оси сочленений в механизме лежат в той же плоскости. То эквивалентно сказать, что все столбцы матрицы Якобиана 3×n, связанные с отображением, определённым в уравнении (4), будут ортогональны данному вектору (нормали к плоскости в вопросе). Следовательно, Якобиан будет неполного ранга, что доказывает теорему. •