Рассмотрим общую постановку задачи построения динамической модели технологического процесса безотносительно к какому-либо реальному процессу. Представим графически рассматриваемый технологический процесс в виде прямоугольника, как это показано на рис. 10.1 На входе одномерного объекта действует случайная функция 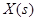 , а на выходе имеем случайную функцию
, а на выходе имеем случайную функцию 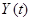 .
.

На входе многомерного объекта действует векторная случайная функция 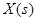 с компонентами
с компонентами  , а на выходе имеем векторную случайную функцию
, а на выходе имеем векторную случайную функцию 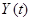 с составляющими
с составляющими 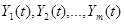 .
.
Задачу построения динамической модели технологического процесса рассмотрим для простейшего одномерного случая. Пусть на входе процесса действует случайная функция 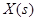 , а на выходе процесса имеем выходную случайную функцию
, а на выходе процесса имеем выходную случайную функцию 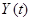 (см. рис. 10.1). Функции
(см. рис. 10.1). Функции 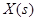 и
и 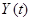 измеримы и в процессе нормального функционирования объекта представляется возможным обеспечить получение реализаций функций
измеримы и в процессе нормального функционирования объекта представляется возможным обеспечить получение реализаций функций 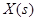 и
и 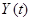 . Ставится задача найти характеристику технологического процесса, приводящую в соответствие функции
. Ставится задача найти характеристику технологического процесса, приводящую в соответствие функции 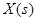 и
и 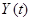 . Такой динамической характеристикой технологического процесса в общем случае является оператор, т.е., закон, в соответствии с которым по одной функции определяется другая функция. Действительно, если известен оператор технологического процесса, то таким образом известна математическая модель процесса, так как известна математическая закономерность превращения
. Такой динамической характеристикой технологического процесса в общем случае является оператор, т.е., закон, в соответствии с которым по одной функции определяется другая функция. Действительно, если известен оператор технологического процесса, то таким образом известна математическая модель процесса, так как известна математическая закономерность превращения 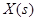 и
и 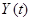 .
.
Соответствие между входными 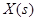 и выходной
и выходной 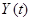 функциями, устанавливаемое оператором
функциями, устанавливаемое оператором  может быть записано сокращенно следующим образом:
может быть записано сокращенно следующим образом:
 (2.1)
(2.1)
Понятие оператора является более общим, чем понятие функции или функционала. Функция ставит в соответствие две переменные величины: например, для функции 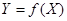 , задавая значение аргумента X, получаем числовое значение функции Y. Функционал ставит в соответствие переменную величину и функцию; например, для функционала
, задавая значение аргумента X, получаем числовое значение функции Y. Функционал ставит в соответствие переменную величину и функцию; например, для функционала  , задавая функцию
, задавая функцию 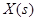 , получим числовое значение функционала Y. Понятие функционала является более общим, чем понятия функции. Еще более общим понятием является понятие оператора, ставящего согласно формуле (2.1) в соответствие две функции. В качестве примеров операторов укажем оператор дифференцирования
, получим числовое значение функционала Y. Понятие функционала является более общим, чем понятия функции. Еще более общим понятием является понятие оператора, ставящего согласно формуле (2.1) в соответствие две функции. В качестве примеров операторов укажем оператор дифференцирования
 (2.2)
(2.2)
оператор интегрирования
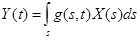 (2.3)
(2.3)
Конкретное представление динамической модели технологического процесса может быть различным и зависит от целей исследования, методов решения конкретной задачи и других факторов. Так, динамическая модель линейного одномерного объекта может быть представлена в виде дифференциального уравнения
 (2.4)
(2.4)
импульсной переходной (весовой) функцией
 (2.5)
(2.5)
частотной характеристикой
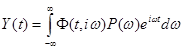 (2.6)
(2.6)
где входная переменная

Каждая из этих динамических моделей дает полное описание линейного одномерного объекта, и эти представления эквивалентны; имея один из видов описания, можно в результате соответствующих преобразований перейти к другому.
На основании сказанного выше очевидно, что под построением динамической модели одномерного технологического процесса понимают нахождение оператора, ставящего в соответствие входную  и выходную
и выходную 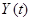 функции объекта. При этом существенно, что при идентификации оператор объекта
функции объекта. При этом существенно, что при идентификации оператор объекта  в формуле (2.1) находится по результатам измерений
в формуле (2.1) находится по результатам измерений  и
и 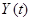 , полученным в процессе нормального функционирования объекта. Результаты измерений
, полученным в процессе нормального функционирования объекта. Результаты измерений  и
и 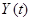 рассматривают как реализацию случайных функций
рассматривают как реализацию случайных функций  и
и 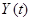 . По реализациям
. По реализациям  и
и 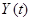 ставится задача определения не самого оператора
ставится задача определения не самого оператора 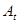 а его оценки
а его оценки  , которая и используется в качестве характеристики неизвестного истинного оператора
, которая и используется в качестве характеристики неизвестного истинного оператора  .
.
Очевидно, что при построении модели, т.е. при определении  , естественно потребовать близости
, естественно потребовать близости  к истинному оператору
к истинному оператору 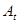 в том смысле, чтобы выход модели
в том смысле, чтобы выход модели 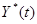 был близок к выходу объекта
был близок к выходу объекта 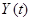 .
.
Для того, чтобы задача могла быть конкретизирована, вводится функция потерь, которая зависит от выходных переменных 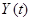 объекта и
объекта и 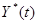 модели, но не зависит от оператора
модели, но не зависит от оператора  .Обозначим эту функцию через
.Обозначим эту функцию через  . Естественно наложить следующее требование: среднее значение (математическое ожидание) функции потерь должно быть наименьшим, т.е.
. Естественно наложить следующее требование: среднее значение (математическое ожидание) функции потерь должно быть наименьшим, т.е.
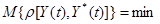 (2.7)
(2.7)
Известно, что в практических приложениях для решения задач точности производства чаще всего принимается критерий минимума среднего квадрата ошибки, т.е. в этом случае функция потерь 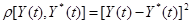 и условие (3) запишется в виде
и условие (3) запишется в виде
 (2.8)
(2.8)
Из статистической динамики известно, что соотношение (2.7) будет выполнено, если потребовать минимума математического ожидания функции 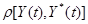 при фиксированной случайной функции
при фиксированной случайной функции  , т.е.
, т.е.
 (2.9)
(2.9)
Тогда достаточным условием минимума соотношения (2.7) будет следующее:
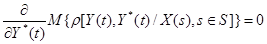 (2.10)
(2.10)
Если в качестве критерия выбрать минимум среднего квадрата ошибки, т.е. потребовать выполнения соотношения (2.8), то, учитывая условие (2.10), получим следующее уравнение для определения оптимальной по этому критерию оценки оператора  .
.
 (2.11)
(2.11)
Из уравнения (2.11) видно, что оператор условного математического ожидания  выходной переменной
выходной переменной 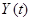 относительно входной переменной
относительно входной переменной  дает оптимальный оператор объекта в классе всех возможных операторов по критерию минимума среднего квадрата ошибки. Таким образом, если по реализациям входной и выходной случайных функций одномерного технологического процесса найти уравнения регрессии выходной переменной
дает оптимальный оператор объекта в классе всех возможных операторов по критерию минимума среднего квадрата ошибки. Таким образом, если по реализациям входной и выходной случайных функций одномерного технологического процесса найти уравнения регрессии выходной переменной 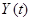 относительно входной
относительно входной  , то получим искомую модель технологического процесса.
, то получим искомую модель технологического процесса.
Будем искать оператор объекта в классе линейных операторов, тогда для получения уравнения, для построения динамической линейной модели умножим обе части уравнения (2.11) на входную случайную функцию 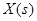

и осредним полученный результат
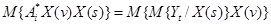 .
.
После осреднения получим
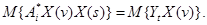 (2.12)
(2.12)
В связи с тем, что оператор  ищется в классе линейных операторов, то оператор математического ожидания (осреднения) М коммутативен с оператором
ищется в классе линейных операторов, то оператор математического ожидания (осреднения) М коммутативен с оператором  .Тогда из уравнения (2.12) получим следующее уравнение для определения оптимальной оценки оператора
.Тогда из уравнения (2.12) получим следующее уравнение для определения оптимальной оценки оператора  в классе линейных операторов по критерию минимума среднего квадрата ошибки:
в классе линейных операторов по критерию минимума среднего квадрата ошибки:
 (2.13)
(2.13)
Для конкретного представления полученного результата для линейной динамической системы, например для получения весовой функции объекта уравнением (2.5), не ограничивая общности, можно предположить, что математические ожидания входной  и выходной
и выходной  переменных равны нулю, т.е.
переменных равны нулю, т.е. 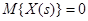 и
и 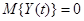 . Согласно определению корреляционной функции случайной функции и взаимной корреляционной функции двух случайных функций в левой части уравнения (2.13) имеем корреляционную функцию входной случайной функции
. Согласно определению корреляционной функции случайной функции и взаимной корреляционной функции двух случайных функций в левой части уравнения (2.13) имеем корреляционную функцию входной случайной функции  , а в правой части - взаимную корреляционную функцию выходной
, а в правой части - взаимную корреляционную функцию выходной 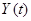 и входной
и входной  случайных функций. Тогда уравнение
случайных функций. Тогда уравнение  может быть переписано следующим образом:
может быть переписано следующим образом:
 (*)
(*)
где 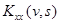 - корреляционная функция
- корреляционная функция  , a
, a  - взаимная корреляционная функция
- взаимная корреляционная функция 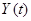 и
и  . При помощи весовой функции
. При помощи весовой функции 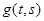 уравнение (*) запишется так:
уравнение (*) запишется так:
 (2.14)
(2.14)
Таким образом, динамическая линейная модель может быть получена путем решения уравнения (2.14), если известны корреляционная функция входной переменной и взаимная корреляционная функция входной и выходной переменных.
Аналогичный результат может быть получен, если использовать представление динамического объекта в виде уравнения (2). Обе части последнего умножим на входную случайную функцию 

и осредним обе части t
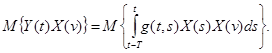 (2.15)
(2.15)
Так как операция математического ожидания и интегрирования коммутативна, то уравнение (2.15) можно представить в виде
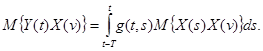
Если теперь предположить, что 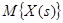 и
и  = 0, а также учесть определения корреляционной и взаимной корреляционной функции, то получим уравнение (2.14).
= 0, а также учесть определения корреляционной и взаимной корреляционной функции, то получим уравнение (2.14).
Практически построение динамической линейной модели значительно упрощается для стационарного объекта, т.е. когда входная и выходная переменные являются стационарными и стационарно связанными. Уравнение (2.13) в этом случае может быть записано в следующем виде:
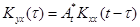
где 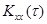 - корреляционная функция стационарной входной случайной функции
- корреляционная функция стационарной входной случайной функции  ,
,  - взаимная корреляционная функция стационарных и стационарно связанных случайных функций входа
- взаимная корреляционная функция стационарных и стационарно связанных случайных функций входа  и выхода
и выхода 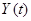 . Весовая функция линейной динамической системы при бесконечном интервале наблюдения в этом случае определяется путем решения интегрального уравнения
. Весовая функция линейной динамической системы при бесконечном интервале наблюдения в этом случае определяется путем решения интегрального уравнения
 (2.16)
(2.16)
для которого выполняется условие физической возможности системы, т.е.  при
при  . Уравнение (2.16) дает оптимальную по критерию минимума среднего квадрата ошибки оценку оператора стационарного объекта. Это уравнение при
. Уравнение (2.16) дает оптимальную по критерию минимума среднего квадрата ошибки оценку оператора стационарного объекта. Это уравнение при 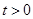 известно как интегральное уравнение Винера-Хопфа. Таким образом, для получения динамической модели стационарного технологического процесса необходимо иметь корреляционную функцию
известно как интегральное уравнение Винера-Хопфа. Таким образом, для получения динамической модели стационарного технологического процесса необходимо иметь корреляционную функцию 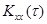 входной стационарной случайной функции Х (s) и взаимную корреляционную функцию
входной стационарной случайной функции Х (s) и взаимную корреляционную функцию  стационарных и стационарно связанных случайных функций входа
стационарных и стационарно связанных случайных функций входа  и выхода
и выхода 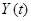 .
.
Сущность аналитического подхода к построению динамической модели заключается в том, что интегральное уравнение2.16 при определенных условиях может быть сведено в интегральному уравнению Вольтерра первого рода типа свертки, которое просто решается при помощи преобразования Лапласа. Пусть по результатам теоретического анализа или статистической обработки экспериментальных данных заданы корреляционная функция 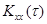 входной случайной функции
входной случайной функции 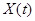 и взаимная корреляционная функция
и взаимная корреляционная функция  входной
входной  и выходной
и выходной 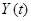 случайных функций. Представим корреляционную функцию
случайных функций. Представим корреляционную функцию  в виде
в виде
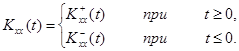 3.1
3.1
Так как корреляционная функция является симметричной функцией аргумента t, то
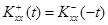 3.2
3.2
и, если корреляционная функция 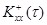 тождественно не равна
тождественно не равна  для всех значений аргумента t при продлении соответствующих ветвей корреляционной функции
для всех значений аргумента t при продлении соответствующих ветвей корреляционной функции  , т.е.
, т.е.
 3.3
3.3
то уравнение2.16 можно свести к уравнению Вольтерра первого рода типа свертки. Условие 3.3 будет выполнено, когда в функцию  будет явно входить модуль t. Аналогично функции 3.1 может быть представлена и взаимная корреляционная функция
будет явно входить модуль t. Аналогично функции 3.1 может быть представлена и взаимная корреляционная функция  :
:
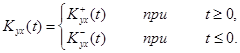 3.4
3.4
при этом естественно, что условие 3.2 не выполняется, так как взаимная корреляционная функция несимметрична.
Заключение
решение математический аппроксимация уравнение
Построение динамической модели одномерного линейного стационарного объекта путем решения интегрального уравнения2.16 базируется на аппроксимации уравнения 2.16 системой линейных алгебраических уравнений. В некоторых случаях, когда заданы корреляционная функция входа  и взаимная корреляционная функция входа и выхода
и взаимная корреляционная функция входа и выхода 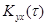 технологического процесса, возможно аналитическое решение уравнения 2.16с целью получения весовой функции технологического процесса, являющейся его динамической характеристикой. Как будет ясно из дальнейшего изложения, аналитическое решение дает возможность подойти к решению задачи по построению типовых динамических характеристик технологических процессов.
технологического процесса, возможно аналитическое решение уравнения 2.16с целью получения весовой функции технологического процесса, являющейся его динамической характеристикой. Как будет ясно из дальнейшего изложения, аналитическое решение дает возможность подойти к решению задачи по построению типовых динамических характеристик технологических процессов.
Сущность постановки задачи построения типовых динамических характеристик заключается в том, что динамические модели технологических процессов, имеющих одинаковые характеристики входных и выходных переменных, очевидно, формально могут быть представлены одной и той же математической моделью. Например, ясно, что если для двух одномерных линейных стационарных технологических процессов, независимо от их физической природы, корреляционные функции входной случайной функции равны и, кроме того, равны также взаимные корреляционные функции входной и выходной случайных функций, то такие два процесса должны иметь идентичное математическое описание, т.е. их весовые функции должны совпадать. Естественно, что это относится не только к объектам, выполняющим одни и те же технологические операции, ной к технологическим процессам, где выполняются разные по своей природе операции. Известно, что. для различных электрических, тепловых, механических и других явлений существует одно и то же математическое описание, дающее возможность решать с достаточной точностью практические задачи.
Очевидно, что решение задачи построения типовых моделей имеет большое практическое значение, так как это создаст условия для построения типовых систем управления и перехода к их серийному производству и массовому применению.
Список литературы
1) В.Н. Нефедов, В.А. Осипова. «Курс прикладной математики», 2012.
2) Я.Б. Зельдович, А.Д. Мышкис. «Элементы прикладной математики», 2010.
) В.Е. Гмурман. «Теория вероятностей и математическая статистика», 2009.