МЕТОДИЧЕСКИЕ УКАЗАНИЯ К
ПРАКТИЧЕСКИМ (СЕМИНАРСКИМ) ЗАНЯТИЯМ
по учебной дисциплине (модулю)
ОСНОВЫНАУЧНЫХ ИССЛЕДОВАНИЙ НА ТРАНСПОРТЕ
Направление подготовки:
Эксплуатация транспортно-технологических машин и комплексов
Профиль подготовки:
Автомобили и автомобильное хозяйство
Квалификация (степень) выпускника: бакалавр
Форма обучения:заочная
Тула 2014 г.
Методические указания к практическим (семинарским) занятиям составлены доц. Хмелевым Р.Н.и обсуждены на заседании кафедры «Автомобили и автомобильное хозяйство» Политехнического института.
протокол №__ от "__"____________ 20 14 _ г.
Зав. кафедрой ________________И.Е. Агуреев
Методические указания к практическим (семинарским) занятиям пересмотрены и утверждены на заседании кафедры «Автомобили и автомобильное хозяйство» Политехнического института.
протокол №___ от "___"____________ 20___ г.
Зав. кафедрой ________________ И.Е. Агуреев
Практическая работа № 1
Оценка случайных погрешностей при многократных измерениях постоянной величины
Цель работы: оценка случайных погрешностей при измерении постоянной физической величины.
Задачи работы:
– знакомство с математической теорией погрешностей;
– статистическая обработка результатов измерений постоянной физической величины.
Теоретический материал:
Результат эксперимента или измерения всегда содержит некоторую погрешность. Если погрешность мала, то ею можно пренебречь. Однако при этом неизбежно возникают два вопроса: во-первых, что понимать под малой погрешностью, и, во-вторых, как оценить величину погрешности.
При измерении любой физической величины производят проверку и установку соответствующего прибора, наблюдение их показаний и отсчет. При этом никогда истинного значения измеряемой величины не получить. Это объясняется тем, что измерительные средства основаны на определенном методе измерения, точность которого конечна. При изготовлении прибора задается класс точности. Его погрешность определяется точностью делений шкалы прибора. Если шкала линейки нанесена через 1 мм, то точность отсчета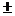 
0,5 мм не изменить если применить лупу для рассматривания шкалы. Аналогично происходит измерение и при использовании других измерительных средств.
Кроме приборной погрешности на результат измерения влияет еще ряд объективных и субъективных причин, обуславливающих появление ошибки измерения - разности между результатом измерения и истинным значением измеряемой величины. Ошибка измерения обычно неизвестна, как неизвестно и истинное значение измеряемой величины. Поэтому одной из важнейших задач математической обработки результатов эксперимента и является оценка истинного значения измеряемой величины по данным эксперимента с возможно меньшей ошибкой.
Если измерения провести многократно в одних и тех же условиях, то результаты отдельных измерений одинаково надежны. Такую совокупность измерений x1, x2 ...xn называют равноточными измерениями.
При многократных (равноточных) измерениях одной и той же величины x случайные погрешности приводят к разбросу получаемых значений xi, которые группируются вблизи истинного значения измеряемой величины Если проанализировать достаточно большую серию равноточных измерений и соответствующих случайных ошибок измерений, то можно выделить четыре свойства случайных ошибок:
1) число положительных ошибок почти равно числу отрицательных;
2) мелкие ошибки встречаются чаще, чем крупные;
3) величина наиболее крупных ошибок не превосходит некоторого определенного предела, зависящего от точности измерения;
4) частное от деления алгебраической суммы всех случайных ошибок на их общее количество близко к нулю, т.е.
На основе перечисленных свойств при учете некоторых допущений математически достаточно строго выводится закон распределения случайных ошибок, описываемый следующей функцией:
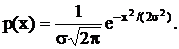
Закон распределения случайных ошибок является основным в математической теории погрешностей. Иначе его называют нормальным законом распределения измеряемых данных (распределением Гаусса). Этот закон в виде графика изображен на рис. 1 а.
а) б)
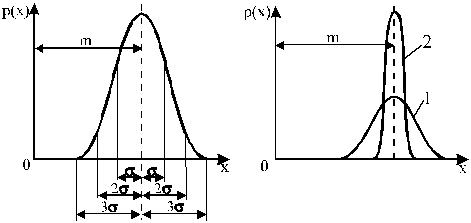
Рис. 1. Характеристики нормального закона распределения
р(x) – плотность вероятности получения отдельных значений xi (сама вероятность изображается площадью под кривой);
m – математическое ожидание, наиболее вероятное значение измеряемой величины x (соответствующее максимуму графика), стремящееся при бесконечно большом числе измерений к неизвестному истинному значению x;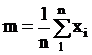 
, где n – число измерений. Таким образом, математическое ожидание m определяется как среднее арифметическое от всех значений xi,
s – среднее квадратическое отклонение измеряемой величины x от значения m;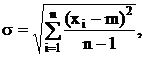 
(xi - m) – абсолютное отклонение xi от m,
Площадь под кривой графика в каком-либо интервале значений x представляет собой вероятность получения случайного результата измерения в этом интервале. Для нормального распределения в интервал ±s (относительно m) попадают 0,62 всех проведенных измерений; в более широком интервале ±2s содержатся уже 0,95 всех измерений, а в интервал ±3s укладываются практически все результаты измерений (кроме грубых ошибок).
Среднее квадратическое отклонение s характеризует ширину нормального распределения. Если повысить точность измерения, разброс результатов резко уменьшится за счет уменьшения s (распределение 2 на рис. 4.1 б уже и острее, чем кривая 1).
Конечной целью эксперимента является определение истинной величины x, к которой при наличии случайных погрешностей можно лишь приблизиться, вычисляя математическое ожидание m для все большего числа экспериментов.
Разброс значений математического ожидания m, вычисленных для различного числа измерений n характеризуется величиной sm;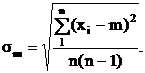 
При сравнении с формулой для s видно, что разброс величины m, как средней арифметической, в Ön меньше разброса отдельных измерений xi. Приведенные выражения для sm и s отражают закон возрастания точности при росте числа измерений. Из него следует, что для повышения точности измерений в 2 раза необходимо сделать вместо одного - четыре измерения; чтобы повысить точность в 3 раза, нужно увеличить число измерений в 9 раз и т.д.
Для ограниченного числа измерений значение m все же отличается от истинного значения величины x, поэтому наряду с вычислением m необходимо указать доверительный интервал, в котором с заданной вероятностью находится истинное значение x. Для технических измерений вероятность 0,95 считают достаточной, поэтому доверительный интервал при нормальном распределении составляет ±2sm. Нормальное распределение справедливо для количества измерений n ³ 30.
В реальных условиях технический эксперимент редко проводится более 5 – 7 раз, поэтому недостаток статистической информации должен компенсироваться расширением доверительного интервала. В этом случае при (n < 30) доверительный интервал определяется как ± kssm, где ks – коэффициент Стьюдента, определяемый по справочным таблицам
С уменьшением числа измерений n коэффициент ks увеличивается, что расширяет доверительный интервал, а при увеличении n значение ks стремится к 2, что соответствует доверительному интервалу нормального распределения ± 2sm.
Конечный результат многократных измерений постоянной величины всегда приводится к виду: m ± kssm.