Пусть имеем следующую задачу.
Задача. Найти распределение в моменты времени t температуры 
в точках x тонкого однородного стержня длины 
(рисунок 4), в котором распространение теплоты описывается уравнением теплопроводности
. (1)
В начальный момент наблюдения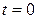 
распределение температуры в точках x стержня имеет вид:
. (2)
За период наблюдения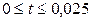 
на концах стержня поддерживалась температура:
. (3)
В уравнениях (2), (3):
; 
.
Поставленная задача содержит начальные и граничные условия, т. е. является смешанной краевой задачей для параболического уравнения теплопроводности (1). Определение температуры 
в точках x стержня в моменты времени t выполним методом конечных разностей.
При решении задачи примем:
- шаг h изменения аргумента x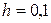 
;
- шаг l изменения аргумента t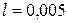 
.
Согласно методу конечных разностей, выполним следующие три этапа:
- дискретизацию задачи;
- алгебраизацию задачи;
- решение разностной задачи.
Дискретизация задачи. На этом этапе выполняется замена области непрерывного изменения аргументов x и t областью дискретного их изменения. Это осуществляется построением в системе координат xOt двух семейств параллельных прямых (рисунок 4):
и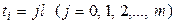 
,
пересечение которых образует область дискретного изменения аргументов x, t в виде множества точек – узлов 
.
В нашей задаче для принятых значени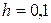й 
и 
имеем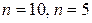 
.
Это множество узлов области определения искомой функции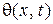 
называют сеточной областью (разностной сеткой или просто сеткой). Функцию 
, значения которой определяют в узлах такой сетки, называют сеточной функцией.
Для сокращения записи и удобства использования дискретные значения аргументов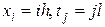 
и сеточной функции 
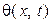обозначают через порядковые номера 
узлов 
сетки и .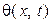
Алгебраизации задачи. На этом этапе метода конечных разностей осуществляется аппроксимация (замена) для каждого внутреннего узла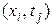 
производных уравнения (1) их конечными разностями. Аппроксимируются также функции начальных и граничных условий (2), (3) с преобразованием их в виде сеточных функций.
В разностных схемах используется понятие шаблона разностных схем. Шаблон является геометрическим представлением совокупности узлов сетки, участвующих в замене исходной дифференциальной задачи в рассматриваемом узле разностной схемой. В зависимости от выбранной схемы узлов для представления производных уравнения (1) в узле их конечными разностями может быть получена одна из двух видов разностных схем: явная и неявная.
 |
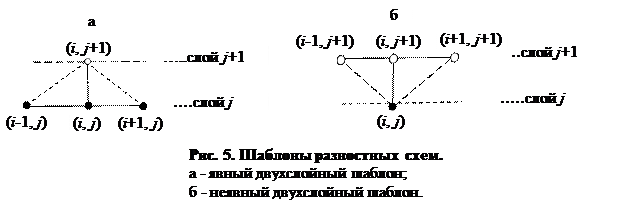На рисунке 5 приведены два шаблона для построения разностной схемы. В шаблоне на рисунке 5, а для определения значения сеточной функции
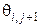в момент времени 
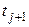используется совокупность узлов сетки, в которых значения сеточной функции 
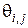в узлах нижнего j –го слоя оси температуры 
являются известными. Они были найдены при выполнении операций вычисления температуры в моменты времени 
с использованием начального условия и граничных условий, начиная с момента при 
.
Такая совокупность узлов сетки, в которых значения сеточной функции в узлах нижнего j –го слоя являются известными, называется явным двухслойным шаблоном и, соответственно, полученная на основе использования такого шаблона разностная схема, называется явной разностной схемой. Она позволяет непосредственно найти значение сеточной функции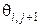 
в следующий момент времени 
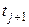по известным её значениям во всех соседних узлах 
, 
, 
нижележащего слоя j.
Разностная схема исходной задачи может быть построена с применением шаблона, в котором искомая сеточная функция θ i , j +1 в рассматриваемом узле сетки 
выражена через её неизвестные значения в соседних узлах и известного ее значения в узле нижнего уровня (рисунок 5, б). Такой шаблон называется неявным двухслойным шаблоном. Так, при использовании неявного двухслойного шаблона при замене дифференциального уравнения (4) его разностным аналогом в узлах получим при задании значений 
систему из (n -1)× m уравнений, в которой известны только значения сеточной функции в узлах 
. Такую разностную схему называют не явной разностной схемой. В этом случае для нахождения решения краевой задачи составляется система уравнений для всех внутренних узлов сеточной области и совместно с уравнениями начальных и граничных условий решается относительно неизвестных значений сеточной функции.
Рассмотрим построение явной и неявной разностных схем для решения поставленной задачи.
Вспомним, что согласно понятию производной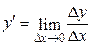 
, ее значение в i - м узле сетки приближенно может быть вычислено по одной из трех формул:
с помощью левых разностей
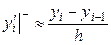, (4)
с помощью правых разностей
, (5)
с помощью центральных разностей
.
При этом производная второго порядка может быть найдена по формуле
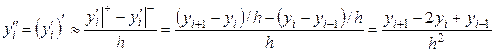. (6)
Построение явной разностной схемы. Применяя явный шаблон а) рисунка 5, заменим производные 
и 
для внутренних узлов их конечными разностями:
;
.
Подставив в уравнение (1) конечные разности их производных, получим
.
В данном уравнении неизвестным является значение сеточной функции 
в узле сетки. Разрешим это уравнение относительно
,
где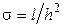 
.
Добавив к этой формуле начальное и граничные условия, записав их применительно к дискретным величинам x, t и сеточной функции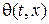 
, получим следующую систему уравнений
(7)
Эта система уравнений является математической формой представления явной разностной схемы нахождения решения уравнения (1). Она позволяет, последовательно задавая координаты узла сетки, непосредственно найти значение сеточной функции 
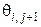в следующий момент времени 
по известным её значениям во всех соседних узлах 
, 
, 
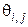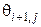нижележащего слоя предыдущего момента времени j.
Построение неявной разностной схемы. Применяя неявный шаблон б) рисунка 5, заменим производные и для внутренних узлов 
их конечными разностями:
;
.
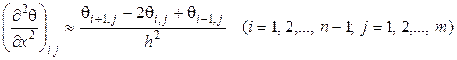Подставив эти конечные разности в соответствующие производные уравнения (1), получим
.
Используя обозначение σ = l / h 2, это уравнение приведем к виду
. (8)
Уравнение (8) описывает распределение искомых значений сеточной функции 
во внутренних узлах построенной сеточной области. Заметим, что в данном уравнении известным является только значение сеточной функции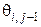 
в узле 
нижнего уровня сетки (рисунок 5, б).
Записывая это уравнение для координаты 
и времени 
каждого внутреннего узла сетки, получим систему из (n -1)× m линейных алгебраических уравнений:
(9)
Эта система уравнений является математической формой представления не явной разностной схемы нахождения решения уравнения (1). Решая эту систему с учетом начального и граничных условий
(10)
относительно неизвестных значений сеточной функции 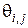во внутренних узлах сеточной области, получим приближенное решение поставленной задачи (1)-(3).
Замечание. При выборе значения величины σ в уравнениях (7), (8) следует учитывать два обстоятельства:
1) погрешность замены дифференциального уравнения разностным должна быть наименьшей;
2) система разностных уравнений должна быть устойчивой, т. е. малые изменения исходных данных не должны вызывать большие изменения решения системы.
Установлено, система уравнений (7) будет устойчивой при 0< σ ≤ 0,5, а система (9) при любом σ. Наиболее простой вид эти системы принимают при σ = 0,5.
Контрольные вопросы и упражнения для приобретения