План лекции
1. Определённый интеграл. Определение с помощью интегральных сумм.
2. Элементы теории меры.
3. Интегрируемость непрерывных функций.
4. Основные свойства определенного интеграла.
o Определённый интеграл. Определение с помощью интегральных сумм.
Множество точек отрезка  таких, что:
таких, что:  , называют разбиением отрезка
, называют разбиением отрезка  .
.
Длины частичных отрезков разбиения обозначим: 
Мелкостью разбиения  (читается – “дельта большое”) назовем максимальную из длин отрезков разбиения, т. е:
(читается – “дельта большое”) назовем максимальную из длин отрезков разбиения, т. е:  .
.
Интегральной суммой функции 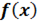 на отрезке
на отрезке 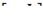 с разбиением
с разбиением  будем называть сумму (зависящую от разбиения
будем называть сумму (зависящую от разбиения  и выбора точек
и выбора точек  ) вида:
) вида:

Определение
Пусть  определена на
определена на  . Разобьём
. Разобьём  на части с несколькими произвольными точками
на части с несколькими произвольными точками  . Тогда говорят, что произведено разбиение
. Тогда говорят, что произведено разбиение 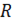 отрезка
отрезка  . Далее выберем произвольную точку
. Далее выберем произвольную точку 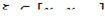 ,
,  ,
,
Определённым интегралом от функции  на отрезке
на отрезке  называется предел интегральных сумм при стремлении ранга разбиения к нулю
называется предел интегральных сумм при стремлении ранга разбиения к нулю  , если он существует независимо от разбиения
, если он существует независимо от разбиения 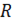 и выбора точек
и выбора точек  , то есть
, то есть

Если существует указанный предел, то функция  называется интегрируемой на
называется интегрируемой на 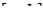 по Риману.
по Риману.
o Элементы теории меры
Один из наиболее важных абстрактных инструментов, который в сочетании с различными математическими дисциплинами служит изучению конкретных моделей, - это «общая» теория меры и интеграла.
Мера множества — неотрицательная величина, интуитивно интерпретируемая как размер (объем) множества. Собственно, мера - это некоторая числовая функция, ставящая в соответствие каждому множеству (из некоторого семейства множеств) некоторое неотрицательное число. Кроме неотрицательности мера, как функция, должна также обладать свойством аддитивности - мера объединения непересекающихся множеств должна равняться сумме их мер. Необходимо отметить, что не всякое множество измеримо - для каждой функции меры обычно подразумевается некоторое семейство множеств (называемых измеримыми по данной мере), для которых мера существует.
Частным случаем меры является мера Лебега для подмножеств, обобщающая понятие объёма (или площади или длины, если или соответственно) на случай множеств, более общих, чем просто ограниченных гладкой поверхностью.
Определение
Пусть задано множество  с некоторым выделенным классом подмножеств
с некоторым выделенным классом подмножеств  . Обычно предполагается, что данный класс подмножеств является как минимум полукольцом (иногда кольцом или алгеброй).
. Обычно предполагается, что данный класс подмножеств является как минимум полукольцом (иногда кольцом или алгеброй).
ü В теории множеств кольцом называют непустую систему множеств 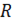 , замкнутую относительно пересечения и симметрической разности конечного числа элементов. Это значит, что для любых элементов A
, замкнутую относительно пересечения и симметрической разности конечного числа элементов. Это значит, что для любых элементов A  из кольца элементы
из кольца элементы  и
и  тоже будут лежать в кольце.
тоже будут лежать в кольце.
ü Алгебра множеств в теории множеств — это непустая система подмножеств, замкнутая относительно операций дополнения (разности) и объединения (суммы).
Функция  называется мерой (иногда объёмом), если она удовлетворяет следующим аксиомам:
называется мерой (иногда объёмом), если она удовлетворяет следующим аксиомам:
1.  — мера пустого множества равна нулю;
— мера пустого множества равна нулю;
2. Для любых непересекающихся множеств 
 — мера объединения непересекающихся множеств равна сумме мер этих множеств (аддитивность, конечная аддитивность).
— мера объединения непересекающихся множеств равна сумме мер этих множеств (аддитивность, конечная аддитивность).
Первая аксиома является удобной, но в некотором смысле "избыточной". Достаточно предположить, что существует хотя бы одно множество с конечной мерой, из чего будет следовать, что мера пустого множества будет равна нулю (в противном случае добавление к любому множеству конечной меры пустого множества изменило бы меру, несмотря на то, что множество не изменилось).
Непосредственно из второй аксиомы следует, что мера объединения любого конечного числа непересекающихся множеств равна сумме мер этих множеств:
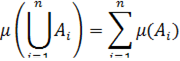
Счётно-аддитивная мера
Из (конечной) аддитивности меры в общем случае не следует, что аналогичное свойство выполнено и для счетного объединения непересекающихся множеств. Выделяют специальный важный класс мер, называемых счетно-аддитивными мерами.
Пусть задано множество  с выделенной δ-алгеброй.
с выделенной δ-алгеброй.
Функция  называется счётно-аддитивной (или δ-аддитивной) мерой, если она удовлетворяет следующим аксиомам:
называется счётно-аддитивной (или δ-аддитивной) мерой, если она удовлетворяет следующим аксиомам:
1. 
2. (δ-аддитивность) Если 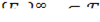 — счётное семейство попарно непересекающихся множеств из
— счётное семейство попарно непересекающихся множеств из  , то есть
, то есть 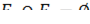 ,
,  то
то
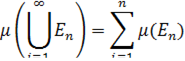
Связанные определения
- Тройка 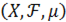 называется пространством с мерой, если
называется пространством с мерой, если  есть измеримое пространство, а
есть измеримое пространство, а  — определённая на нём мера.
— определённая на нём мера.
- Если  является вероятностной мерой, то такое пространство с мерой называется вероятностным пространством.
является вероятностной мерой, то такое пространство с мерой называется вероятностным пространством.
Примеры
- Мера Жордана — пример конечно-аддитивной меры.
- Мера Лебега — пример счетно-аддитивной меры.
- Вероятность — пример конечной меры.
- Мера Хаусдорфа
- Мера Стилтьеса
- Мера Бореля
- Мера Хаара
- Ультрафильтр может быть определён как конечно-аддитивная мера со значениями в множестве из двух элементов 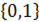
o Интегрируемость непрерывных функций
Теорема:
Если функция 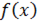 непрерывна на отрезке [a, b], то она интегрируема на нем.
непрерывна на отрезке [a, b], то она интегрируема на нем.
Доказательство:
Так как функция  непрерывна на отрезке [a, b], то по теореме Кантора она равномерно непрерывна на нем. Выберем произвольное как угодно малое ε > 0. Согласно следствию из теоремы Кантора для положительного числа
непрерывна на отрезке [a, b], то по теореме Кантора она равномерно непрерывна на нем. Выберем произвольное как угодно малое ε > 0. Согласно следствию из теоремы Кантора для положительного числа 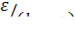 найдется δ > 0 такое, что при разбиении отрезка [a, b] на частичные отрезки
найдется δ > 0 такое, что при разбиении отрезка [a, b] на частичные отрезки 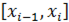 , длина которых
, длина которых  , все колебания
, все колебания 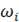 меньше
меньше  . Отсюда
. Отсюда
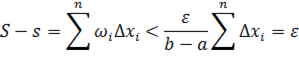
при λ < δ.
Следовательно, для непрерывной на отрезке [a, b] функции 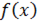 выполнено достаточное условие интегрируемости, а из него вытекает существование определенного интеграла.
выполнено достаточное условие интегрируемости, а из него вытекает существование определенного интеграла.
o Основные свойства определенного интеграла
1. 
2. 
3. Если 
4. Если  – интегрируемы на
– интегрируемы на 
a) 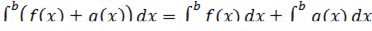
b) Существует 
5. Если существует 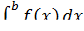 и
и 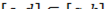 , то существует
, то существует 
6. Если 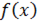 – интегрируема на
– интегрируема на 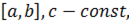 то:
то: 
7. Если существуют  , то существует
, то существует 
Контрольные вопросы:
1. Что такое определенный интеграл?
2. Дать определение с помощью интегральных сумм.
3. Перечислить основные свойства определенного интеграла.
4. Что такое мера множества? Элементы теории меры.
5. Какая функция называется счетно-аддитивной?
6. Интегрируемость непрерывных функций.
ЛЕКЦИЯ 18: