Несобственный интеграл выражает площадь бесконечно длинной криволинейной трапеции.

Примеры:

Вычислить несобственный интеграл или установить его расходимость.

Решение:

Подынтегральная функция 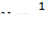непрерывна на интервале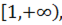

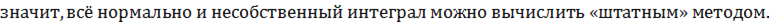
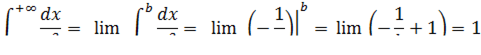
сходящийся несобственный интеграл 1-го типа

Вычислить несобственный интеграл или установить его расходимость.

Решение:

Подынтегральная функция непрерывна на интервале :

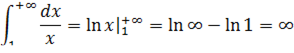
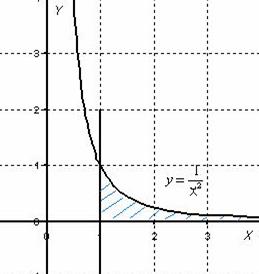
То есть, несобственный интеграл расходится, и площадь заштрихованной криволинейной трапеции равна бесконечности.

расходящийся несобственный интеграл 1-го типа

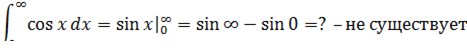
- Несобственный интеграл второго типа

Несобственные интегралы второго рода коварно «шифруются» под обычный определенный интеграл и выглядят точно так же:

Но, в отличие от определенного интеграла, подынтегральная функция терпит бесконечный разрыв (не существует):

1) в точке ,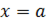

2) или в точке ,

3) или в обеих точках сразу,

4) или даже на отрезке интегрирования.

1. Если подынтегральной функции не существует в точке :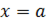

Сразу пример, чтобы было понятно:

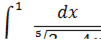
Вроде бы это определенный интеграл. Но на самом деле – это несобственный интеграл второго рода, если мы подставим в подынтегральную функцию значение нижнего предела , то знаменатель у нас обращается в ноль, то есть подынтегральной функции просто не существует в этой точке!

Вообще при анализе несобственного интеграла всегда нужно подставлять в подынтегральную функцию оба предела интегрирования. В этой связи проверим и верхний предел:

Здесь всё хорошо.

Криволинейная трапеция для рассматриваемой разновидности несобственного интеграла принципиально выглядит так:

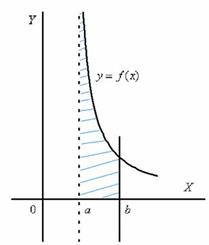
Здесь почти всё так же, как в интеграле первого рода.

Этот интеграл численно равен площади заштрихованной криволинейной трапеции, которая не ограничена сверху. При этом могут быть два варианта: несобственный интеграл расходится (площадь бесконечна) либо несобственный интеграл равен конченому числу (то есть, площадь бесконечной фигуры – конечна!).

Пример: Вычислитьнесобственный интеграл и установить его расходимость.

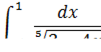
Решение:

Подынтегральная функция терпит бесконечный разрыв в точке .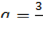

Сначала вычислим неопределенный интеграл:

Вычислим несобственный интеграл:

Что здесь нового? По технике решения практически ничего. Единственное, что поменялось, это запись под значком предела: . Добавка обозначает, что мы стремимся к значению справа. Такой предел в теории пределов называют односторонним пределом. В данном случае у нас правосторонний предел.

Подставляем верхний и нижний предел по формуле Ньютона-Лейбница.

Разбираемся с 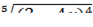при . Как определить, куда стремиться выражение? Грубо говоря, в него нужно просто подставить значение , подставляем три четверти и указываем, что

В данном случае несобственный интеграл равен отрицательному числу. В этом никакого криминала нет, просто соответствующая криволинейная трапеция расположена под осью .

Геометрический смысл несобственных интегралов II типа: