Лабораторная работа №1
МАТЕМАТИЧЕСКИЕ МОДЕЛИ ЛИНЕЙНЫХ СИСТЕМ
АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
1. ЦЕЛЬ РАБОТЫ
Ознакомиться с пакетом моделирования MatLAB. Освоить основные приемы моделирования систем автоматического управления.
2. КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
Поведение динамической линейной системы автоматического управления может быть описано скалярным дифференциальным уравнением n-го порядка
| (1.1) |
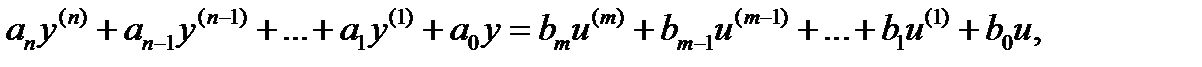
где y– выходная переменная; u – входной сигнал; m – порядок производной входного сигнала; ai и bj – постоянные коэффициенты.
При условии, что m<n, уравнение (1.1) можно записать в виде системы уравнений первого порядка
| (1.2) |
где xi– координаты вектора состояния, aij и bi – постоянные коэффициенты.
Система уравнений (1.2) может быть представлена в компактной векторно-матричной форме
| (1.3) |
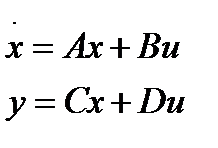
где A – n х n – мерная матрица постоянных коэффициентов системы; В – n х 1 – мерная матрица постоянных коэффициентов входа; c – 1 х n – мерная матрица постоянных коэффициентов выхода; X – n -мерный вектор состояния.
4. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
4.1. Ознакомиться с пакетом прикладных программ MATLAB (см. Приложение А).
4.2 Ознакомиться с методом интегрирования обыкновенных дифференциальных уравнений (OrdinaryDifferentialEquations - ODE) методами Эйлера и Рунге-Кутты (см. Приложение Б).
4.3. В соответствии с вариантом задания (см. табл.1.1) построить схему моделирования линейной системы автоматического управления, используя уравнения (1.1.-1.3).
Например, система 3-го порядка описывается соответствующим дифференциальным уравнением:
+ 
= 
Для решения в пакете МатЛаб преобразуем его в систему из трех дифференциальных уравнений 1-го порядка:
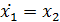
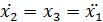
Тогда решение уравнения находится в виде вектора-столбца:
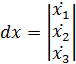
4.4. Создать на жестком диске директорию по собственным именем.
Активировать пакет МатЛаб. Выбрать вкладку NewScript. Набрать скрипт следующего вида (в зависимости от варианта):
function[dx]=ode(t,x)
a0=…
a1=…
a2=…
a3=…
b=…
y=… / либо 1,либоsin(t) /
dx=zeros(3,1) / обнуление массива dx[3,1] /
dx(1)=x(2)
dx(2)=x(3)
dx(3)=(b*y-a0*x(1)-a1*x(2)-a2*x(3))/a3
end
Сохранить как файл всвоей директории (не на рабочем столе), например, под именем «ode.m».
4.5 Набрать еще один скрипт следующего вида:
[t,x]=ode45(‘ode’,[0 10],[0.1 0.5 0])
/ ‘ode’ – имя 1-го скрипта
/ [0 10] – интервал времени расчета функции
/ [0.1 0.5 0] – начальные условия (в данном случае, ненулевые)
plot(t,x(:,1),'b-',t,x(:,2),’g—‘,t,sin(t),’LineWidth’,2)
/ на одном графике строим функцию x=x1, ее производную x2 и сигнал возмущения y=sin(t) (либо y=1)
legend(‘x_1(t)’,‘x_2(t)’)
grid on
xlabel(‘t, c’)
ylabel(‘x_i(t)’)
title(‘Реакция системы на входной сигнал y=sin(t) при начальных условиях[1 0.5 0.5]’)
Сохранить скрипт в ту же директорию, запустить на исполнение.
4.6. Осуществить моделирование системы при двух видах входных воздействий:
а) y = 1(t). Начальные условия нулевые. При этом график функции 
будет являться графиком переходной характеристики 
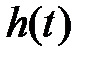, а график функции 
будет являться графиком импульсной переходной функции 
. На монитор выводить графики сигналов , 
и y(t). Продолжительности интервалов наблюдения выбрать самостоятельно (например, от 0 до 10).
б) y = sin (t). Начальные условия нулевые. На монитор выводить графики сигналов и y(t). Продолжительности интервалов наблюдения выбрать самостоятельно.
4.7. Осуществить моделирование свободного движения системы с ненулевыми начальными условиями (в соответствии с вариантом - см. табл.1.2). Снять выходные характеристики x(t) системы автоматического управления.
Таблица 1.1
Варианты параметров моделей
| Вариант | ||||||||||||
| порядок модели n | ||||||||||||
| a0 | 0,12 | |||||||||||
| a1 | 0,5 | 0,5 | 0,8 | |||||||||
| a2 | 0,5 | |||||||||||
| a3 | - | - | - | - | - | - | ||||||
| b0 | 2,5 | 7,5 | 0,1 |
При программировании в математическом пакете MatLab дробная часть отделяется от целой точкой, а не запятой.
Таблица 1.2
Варианты начальных условий моделей
| Вариант | ||||||||||||
| Порядок модели n | ||||||||||||
| x(0) | ||||||||||||
| x(1) (0) | 0,5 | -0,2 | -0,4 | 0,1 | -0,5 | 0,5 | 0,4 | -0,5 | 0,5 | |||
| x(2) (0) | 0,1 | 0,2 | -0,1 | 0,1 | - | - | - | - | - | - |
5.СОДЕРЖАНИЕ ОТЧЕТА
Отчет должен содержать следующие разделы:
1. Цель работы.
2. Порядок выполнения работы.
3. Математическая модель динамической системы.
4. Графики переходных процессов.
5. Выводы.
6.ВОПРОСЫДЛЯ САМОКОНТРОЛЯ
6.1. Какую систему можно считать линейной?
6.2. Что значит найти численное решение дифференциальногоуравнения?
6.3. Найти передаточную функцию системы, динамика которой описывается дифференциальным уравнением y(1)+3y=2u(1)+5u. Представить это уравнение в пространстве состояний и в матричном виде.
6.4. Метод интегрирования реализуется функцией ode45, что означает 4 и 5, каким образом гарантируется заданная точность решения?
6.5. Показать на графике (посчитать вручную) как, зная начальные условия х(0) и у(0), получить следующую точку х(1) и у(1) методом Эйлера, модифицированным методом Эйлера, методом Рунге-Кутты 4 порядка.
Приложение А
СИСТЕМА MatLAB
Настоящее приложение содержит описание некоторых функций системы MatLAB, позволяющих моделировать технические системы и получать их характеристики в наглядном виде.
MatLAB (сокращение от MatrixLaboratory – матричная лаборатория) – это компьютерная система проведения математических расчетов, получившая широкое распространение.
Интегрирование системы обыкновенных дифференциальных уравнений
Интегрирование системы обыкновенных дифференциальных уравнений осуществляется при помощи функций ode23 и ode45. Функция ode23 осуществляет интегрирование численным методом Рунге-Кутта 2-го порядка, а с помощью метода 3-го порядка контролирует относительные и абсолютные ошибки интегрирования на каждом шаге и изменяет величину шага интегрирования так, чтобы обеспечить заданные пределы ошибок интегрирования. При использовании функции ode45 интегрирование осуществляется методом Рунге-Кутта 4-го порядка, а величина шага контролируется методом 5-го порядка.
Система дифференциальных уравнений должна быть представлена в форме Коши:
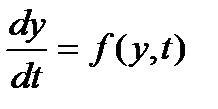(1.1)
где y – вектор переменных состояния системы, t – аргумент (обычно время), f – нелинейная вектор-функция от переменных состояния у и аргумента t.
Обращение к процедурам численного интегрирования имеет вид:
[t, y] = ode23(‘<имяфункции>’, tspan, y0, options)
[t, y] = ode45(‘<имяфункции>’, tspan, y0, options),
где<имя функции> - имя M-файла, являющегося функцией Matlab от t и y, в котором вычисляется вектор функция f(y,t), т.е. правые части системы дифференциальных уравнений;
tspan – вектор задающий интервал интегрирования [t0 tfinal], t0 – начальное значение интервала, tfinal – конечное;
yo – вектор начальных условий;
options – строка параметров, определяющих значения допустимой относительной и абсолютной погрешности интегрирования. Этот параметр можно не указывать, если пользователя устраивают значения погрешностей, заданных по умолчанию, т.е. относительная погрешность интегрирования 1.0e-3, а абсолютная (по каждой из переменных состояния) – 1.0e-6. В противном случае, перед обращением к процедуре ode23 следует указать значения погрешностей при помощи процедуры odeset.
Результатом интегрирования является матрица проинтегрированных значений фазовых переменных y, в которой каждый столбец соответствует одной из переменных состояния, а строка содержит значения переменных состояния, соответствующих определенному шагу интегрирования, т.е. значению вектора t.
Рассмотрим пример:
Пусть задана система обыкновенных дифференциальных уравнений:
со следующими начальными условиями:
Для интегрирования данной системы уравнений необходимо создать М-файл, который является функцией переменных t и y. Для создания файла воспользуемся редактором MATLABEditor/Debugger, который вызывается из основного меню File – New – M-File. Текстфайла:
functiondy=rigid(t,y)
dy=zeros(3,1);
dy(1)=y(2)*y(3);
dy(2)=-y(1)*y(3);
dy(3)=-0.51*y(1)*y(2);
Название файла и функции должны совпадать. Файл надо сохранить с названием rigid.
В этом примере абсолютная и относительная погрешность задается при помощи команды odeset, время интегрирования зададим в интервале от 0 до 12 [0 12], вектор начальных условий [0 1 1]. Для осуществления процедуры интегрирования в рабочем пространстве Matlab необходимо набрать:
» options=odeset('RelTol',1e-4,'AbsTol',[1e-4 1e-4 1e-5]);
» [t,y]=ode45('rigid',[0 12],[0 1 1],options);
Чтобы просмотреть результаты в рабочем пространстве Matlab необходимо ввести в командной строке y. Графически результаты выводятся при помощи команды plot:
» plot(t,y(:,1),'-',t,y(:,2),'-.',t,y(:,3),'.').
Синтаксис:
plot(y)
plot(x, y)
plot(x, y, s)
plot(x1, y1, s1, x2, y2, s2,...)
Описание:
Команда plot(y) строит график элементов одномерного массива y в зависимости от номера элемента; если элементы массива y комплексные, то строится график plot(real(y), imag(y)). Если Y - двумерный действительный массив, то строятся графики для столбцов; в случае комплексных элементов их мнимые части игнорируются.
Команда plot(x, y) соответствует построению обычной функции, когда одномерный массив x соответствует значениям аргумента, а одномерный массив y - значениям функции. Когда один из массивов X или Y либо оба двумерные, реализуются следующие построения:
- если массив Y двумерный, а массив x одномерный, то строятся графики для столбцов массива Y в зависимости от элементов вектора x;
- если двумерным является массив X, а массив y одномерный, то строятся графики столбцов массива X в зависимости от элементов вектора y;
- если оба массива X и Y двумерные, то строятся зависимости столбцов массива Y от столбцов массива X.
Команда plot(x, y, s) позволяет выделить график функции, указав способ отображения линии, способ отображения точек, цвет линий и точек с помощью строковой переменной s, которая может включать до трех символов из следующей таблицы:
| Тип линии | Тип точки | Цвет | ||||||||||||||||||||||||||||||||||
|
|
|
Если цвет линии не указан, он выбирается по умолчанию из шести первых цветов, от желтого до синего, повторяясь циклически.
Команда plot(x1, y1, s1, x2, y2, s2,...) позволяет объединить на одном графике несколько функций y1(x1), y2(x2),..., определив для каждой из них свой способ отображения.
Обращение к командам plot вида plot(x, y, s1, x, y, s2) позволяет для графика y(x) определить дополнительные свойства, для указания которых применения одной строковой переменной s1 недостаточно, например при задании разных цветов для линии и для точек на ней.
Примеры:
Построим график функции y = sin(x) на отрезке [-pp ] с шагом p /500:
x = -pi:pi/500:pi;
y = sin(x);
plot(y)
plot(x, y)
Для вывода в одно окно нескольких графиков необходимо ввести команду holdon, для отмены — команду holdoff.
Для создания нового графического окна необходимо ввести команду figure(i), где i — номер графического окна. Эта же команда используется для активизации уже созданного окна с номером i.
Для введения комментария к графикам можно воспользоваться командой legend.
Синтаксис:
legend(‘<текст1>‘, ‘<текст2>‘, ‘<текст3>‘,...)
legend(‘<типлинии1>‘, ‘<текст1>‘, ‘<типлинии2>‘, ‘<текст2>‘,...)
legend(h,...)
legend(M)
legend(h, M)
legend off
legend(..., n)
Описание:
Команда legend(‘<текст1>‘, ‘<текст2>‘, ‘<текст3>‘,...) добавляет к текущему графику пояснение в виде указанных текстовых строк.
Команда legend(‘<тип линии1>‘, ‘<текст1>‘, ‘<тип линии2>‘, ‘<текст2>‘,...) позволяет специфицировать тип линии, которая выносится в пояснение, так, как это делается в команде plot.
Команда legend(h,...) добавляет пояснение к графику с дескриптором h.
Команды legend(M) и legend(h, M), где M - массив строк, также допустимы для формирования пояснения. Следует помнить, что строки массива M должны иметь одинаковую длину.
Команда legendoff удаляет пояснение с текущего графика.
Команда legend(..., n) устанавливает предельное количество позиций для размещения пояснения. Если оказывается, что в области графика места недостаточно, график перестраивается и пояснение размещается вне пределов графика. Если n = -1, то пояснение размещается вне области графика. Если n = 0, то пояснение размещается в области графика, если места для этого достаточно.
Для перемещения пояснения следует нажать левую кнопку мыши, находясь в этой области, а затем переместить пояснение в нужную позицию.