Переходной процесс системы

step(W) – нахождение реакции системы sys на единичное ступенчатое воздействие.

Амплитудно-фазовую характеристику системы в полярных координатах можно получить воспользовавшись командой

nyquist(W).

Логарифмическую амплитудно-фазовую характеристику системы в полярных координатах можно получить воспользовавшись командой

bode(W).

Для того чтобы построить переходной процесс системы, т.е. ее реакцию на единичное ступенчатое воздействие, а также ее частотные характеристики в одном окне используется так называемый интерактивный наблюдатель ltiview (для этого нужно набрать в рабочем окне команду ltiview и на экране появится окно интерактивного обозревателя). При первом обращении к обозревателю окно пусто, т.к. нужно импортировать в него модель системы.

Для этого из верхнем меню File необходимо выбрать команду import – на экране появится меню выбора импортируемой модели системы (напримерW).

Обозреватель позволяет получить на одном экране несколько графиков, в том числе и частотные характеристики системы. Для выбора необходимых характеристик требуется выбрать из меню Tools команду ViewerConfiguration.

На экране появятся различные конфигурации количества отображаемых графиков. Если выбрать нажатием радио-кнопки конфигурацию, содержащую 4 графика, тогда на экране появятся следующие графики:

· переходной процесс;

· импульсная переходная функция (реакция системы на дельта-функцию);

· логарифмическая амплитудно-фазовая частотная характеристика;

· амплитудно-фазовая частотная характеристика в полярных координатах.

Приложение Б

Метод Эйлера. Усовершенствованный метод Эйлера.
Классический метод Рунге-Кутты

Перечисленные в заголовке методы предназначены для приближённого нахождения решений дифференциальных уравнений, систем ДУ, краткая постановка наиболее распространённой задачи такова:

Рассмотрим дифференциальное уравнение первого порядка 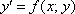, для которого требуется найти частное решение, соответствующее начальному условию 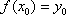. Что это значит? Это значит, нам нужно найти функцию (предполагается её существование), которая удовлетворяет данному дифф. уравнению, и график которой проходит через точку .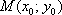

Но переменные в уравнении 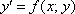разделить невозможно. Никакими известными способами. А если и возможно, то получается неберущийся интеграл. Однако частное решение существует.Здесь на помощь приходят методы приближенных вычислений, которые позволяют с высокой точностью «сымитировать» функцию на некотором промежутке.

Идея методов Эйлера и Рунге-Кутты состоит в том, чтобы заменить фрагмент графика ломаной линией. Рассмотрим И сторически первого и самый простой метод:

Задание

Найти частное решение дифференциального уравнения 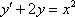, соответствующее начальному условию 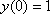, методом Эйлера на отрезке 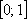с шагом 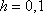. Построить таблицу и график приближённого решения.

Во-первых, перед нами обычное линейное уравнение, которое можно решить стандартными способами, и поэтому можно сразу же найти точное решение:

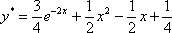– можно выполнить проверку и убедиться, что данная функция удовлетворяет начальному условию 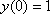и является корнем уравнения .

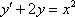Что нужно сделать? Нужно найти и построить ломаную, которая приближает график функции 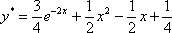на промежутке 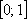. Поскольку длина этого промежутка равна единице, а шаг составляет 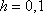, то наша ломаная будет состоять из 10 отрезков:

причём, точка 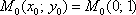уже известна – она соответствует начальному условию 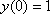. Кроме того, очевидны «иксовые» координаты других точек:

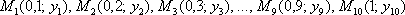
Осталось найти 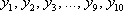.Никакого дифференцирования и интегрирования – только сложение и умножение. Каждое следующее «игрековое» значение получается из предыдущего по простой рекуррентной формуле:

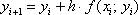
Представим дифференциальное уравнение 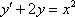в виде :

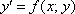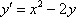
Таким образом: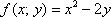

«Раскручиваемся» от начального условия :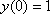

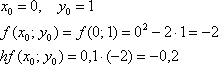
Далее:

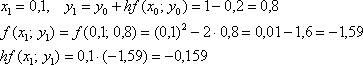
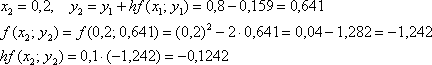
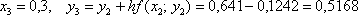
и так далее.

Результаты вычислений удобно заносить в таблицу:

По результатам 2-го и 3-го столбцов изобразим на чертеже 11 точек 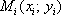и 10 отрезков, соединяющих смежные точки. Для сравнения построим график точного частного решения :

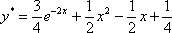Существенным недостатком простого метода Эйлера является слишком большая погрешность, при этом легко заметить, что погрешность имеет тенденцию накапливаться – чем дальше мы уходим от точки 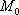, тем преимущественно больше становится расхождение между приближением и истиной. Это объяснимо самим принципом, который Эйлер положил в основу своего метода: отрезки параллельны соответствующим касательным к графику функции в точках 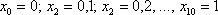. Данный факт хорошо просматривается по чертежу.

Как можно улучшить приближение? Первая мысль – измельчить разбиение. Разделим отрезок 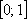, например, на 20 частей. Тогда шаг составит: 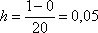, и совершенно понятно, что ломаная из 20 звеньев заметно точнее приблизит частное решение. С помощью того же Экселя не составит труда обработать промежуточные отрезки, однако зададимся вопросом: а нельзя ли КАЧЕСТВЕННО улучшить метод?