Оглавление
Основные сведения о цепях Маркова. 3
Решение системы дифференциальных уравнений Колмогорова аналитическими методами. 5
Метод Рунге-Кутта численного решения дифференциальных уравнений. 7
Задания. 8
Порядок выполнения курсовой работы.. 9
Состав и содержание пояснительной записки. 9
Вопросы для самопроверки. 10
Литература. 11
Основные сведения о цепях Маркова
Пусть физическая система 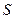 может находиться в одном из состояний, образующих конечное множество
может находиться в одном из состояний, образующих конечное множество 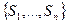 , и переходит из одного состояний в другое
, и переходит из одного состояний в другое 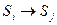 в строго определенные моменты времени
в строго определенные моменты времени 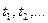 Тогда говорят, что в этой системе происходит случайный процесс.
Тогда говорят, что в этой системе происходит случайный процесс.
Важным классом случайных процессов являются Марковские случайные процессы (процессы без последействия). Особенность Марковских процессов заключается в том, что прогноз о будущем состоянии системы зависит только от того, в каком состоянии находится система в текущий момент, и не зависит от того, в каких состояниях находилась система в прошлом.
В том случае, когда множество состояний конечно, а переход происходит в строго определенные, изолированные моменты времени 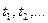 , такой случайный процесс называют Марковской цепью с дискретным временем и конечным числом состояний. (см. примеры в [1])
, такой случайный процесс называют Марковской цепью с дискретным временем и конечным числом состояний. (см. примеры в [1])
Символом 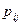 обозначим вероятность перехода системы из состояния
обозначим вероятность перехода системы из состояния 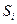 в состояние
в состояние 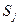 за один шаг. Для случая, когда число состояний в рассматриваемой Марковской цепи
за один шаг. Для случая, когда число состояний в рассматриваемой Марковской цепи  , цепь можно задать матрицей вероятностей переходов за один шаг:
, цепь можно задать матрицей вероятностей переходов за один шаг:
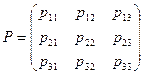 (1)
(1)
В том случае, когда вероятности перехода 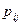 не зависят от номера шага, на котором осуществляется переход
не зависят от номера шага, на котором осуществляется переход 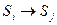 , цепь называется однородной. Элементы матрицы (1) обладают следующими свойствами:
, цепь называется однородной. Элементы матрицы (1) обладают следующими свойствами:
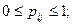
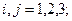

Одна из главных целей исследования Марковских цепей это нахождение закона распределения вероятностей состояний – т.е. найти вероятность для каждого состояния, в котором будет находиться система через конечное число переходов.
Распределение вероятностей состояний Марковской цепи, не изменяющееся со временем, называется стационарным.
Если система  может переходить из одного состояния в другое не в строго определенные, а в произвольные моменты времени, причем множество таких моментов является непрерывным, и выполняется марковское свойство, то такая система называется Марковским процессом с непрерывным временем. Здесь, как и прежде, исследуются вероятности состояний системы, но не за конечное число переходов, а через определенный момент времени.
может переходить из одного состояния в другое не в строго определенные, а в произвольные моменты времени, причем множество таких моментов является непрерывным, и выполняется марковское свойство, то такая система называется Марковским процессом с непрерывным временем. Здесь, как и прежде, исследуются вероятности состояний системы, но не за конечное число переходов, а через определенный момент времени.
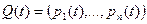 - матрица вероятностей состояний системы
- матрица вероятностей состояний системы 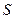 в момент времени
в момент времени 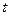 .
.  - вероятность того, что в момент времени
- вероятность того, что в момент времени 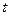 система будет находиться в состоянии
система будет находиться в состоянии 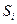 . Для того, что бы найти
. Для того, что бы найти  , нужно знать характеристики процесса, аналогичные вероятностям перехода
, нужно знать характеристики процесса, аналогичные вероятностям перехода 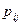 для дискретного случая. Для Марковского процесса с непрерывным определяющим параметром является интенсивность перехода
для дискретного случая. Для Марковского процесса с непрерывным определяющим параметром является интенсивность перехода  из состояния
из состояния 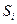 в состояние
в состояние  .
.
Интенсивностью перехода  системы
системы 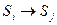 называется предел
называется предел
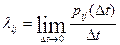 , (2)
, (2)
где 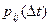 - вероятность перехода
- вероятность перехода 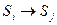 (
(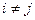 ) на интервале времени
) на интервале времени 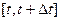 .
.
Величины  при
при 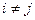 , в общем случае, зависят от расположения интервала
, в общем случае, зависят от расположения интервала 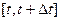 на оси времени (т.е. являются функциями времени). Если
на оси времени (т.е. являются функциями времени). Если  не меняется с течением времени при
не меняется с течением времени при 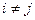 , то Марковская цепь называется однородной.
, то Марковская цепь называется однородной.
Рассмотрим матрицу интенсивностей переходов для Марковской цепи с  .
.
Элементы матрицы интенсивностей 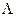 удовлетворяют условиям:
удовлетворяют условиям: 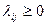 при
при 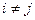 ,
,  при
при 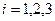 ,
, 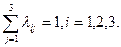
Матрица вероятностей состояний 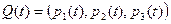 удовлетворяет системе дифференциальных уравнений Колмогорова. В координатной форме:
удовлетворяет системе дифференциальных уравнений Колмогорова. В координатной форме:
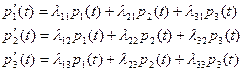 (3)
(3)
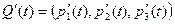 - матрица, составленная из производных
- матрица, составленная из производных 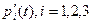 вероятностей в момент времени
вероятностей в момент времени 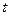 . Для решения системы (3) необходимо, как обычно, задать начальные условия:
. Для решения системы (3) необходимо, как обычно, задать начальные условия:
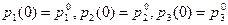 , где
, где 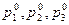 - заданные числа, и
- заданные числа, и 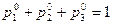 .
.
Распределение вероятностей называется стационарным, если вероятности 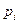 состояний
состояний 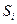 не зависят от времени:
не зависят от времени: 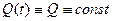 . Доля стационарного распределения вероятностей
. Доля стационарного распределения вероятностей 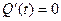 , тогда можно записать:
, тогда можно записать:
 , или в координатной форме:
, или в координатной форме:
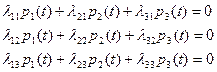 (4)
(4)
Кроме стационарных вероятностей состояний иногда полезно знать, как будут вести себя вероятности состояний при неограниченном возрастании времени: 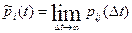 , вероятности
, вероятности 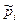 называются предельными (или финальными) вероятностями системы.
называются предельными (или финальными) вероятностями системы.
Состояние в Марковской цепи называется существенным, если выйдя из этого состояния, система может в него вернуться за один или несколько шагов, в противном случае состояние называется несущественным.
Марковская цепь называется регулярной, если из одного существенного состояния можно попасть в любое другое существенное состояние за конечное число шагов [1,2].