Тема: Использование свойств и графиков функций при решении уравнений и неравенств.
Для решения уравнений и неравенств можно пользоваться аналитическим и графическим способами. Но, несмотря на способ, который Вы выберете, необходимо учитывать свойства функций и вид их графиков.
 Свойства функций
Свойства функций
Четность/ нечетность
Если функция на графике является симметричной относительно оси ОУ, то данная функция будет называться парной. Для такой функции значение функции будет одинаковым, как для положительных "х", так и для отрицательных.
f(-x) = f(x).

Четной функцией можно назвать квадратичную функцию, графиком которой является парабола с вершиной в начале координат. Так же график выражения в модуле будет являться парной функцией. Среди тригонометрических функций существует единственная функция, которую можно назвать парной - косинус без сдвига фаз.
Если функция симметрична относительно начала координат, то её называют нечетной.
f(-x) = - f(x).
К таким функциям можно отнести любую функцию, старший член которой будет иметь нечетную степень или же, например, функция синуса.
Множество остальных функций нельзя отнести ни к четным, ни к нечетным.
Периодичность
Если некоторая функция повторяется через некоторый период. Такие функцию будут повторяться до бесконечности. К периодичным функциям относятся все тригонометрические функции, не ограниченные на некотором промежутке. 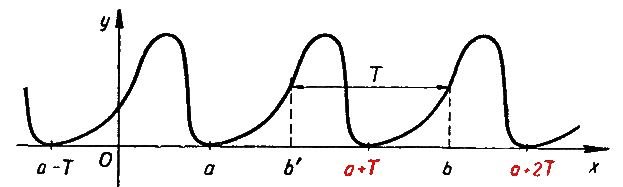
Нули функции и промежутки знакопостоянства
Нуль функций - это такое значение ординаты, при которой функция обращается в нуль.
Когда мы находим решение уравнений, мы, как раз, находим нули функций. Иными словами, нулем называется точка, в которой график функции пересекает ось ОХ.
Промежутки знакопостоянства - это диапазон, в котором функция имеет одинаковый знак, то есть принимает только положительные, или только отрицательные значения.
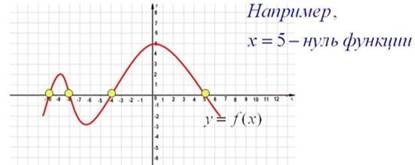
Нули функции разбивает всю числовую прямую на интервалы. Именно относительно нулей происходит решение неравенств высоких степеней. Чередование знаков на промежутках происходит именно относительно нулей функции.
Судя по указанному графику, если нам необходимо найти решение неравенств, где функция будет больше нуля, нам подходят диапазоны
(-10; -8), (-4; 5).
Убывание/ возрастание функции
Если на некотором промежутке [а,б] функция f(x1) < f(x2) для любых x1 < x2, то такую функцию называют монотонно возрастающей.
Если на некотором промежутке [а,б] функция f(x1) > f(x2) для любых x1 < x2, то такую функцию называют монотонно убывающей.
5. Минимум/ максимум/ экстремум. Если для некоторого участка функции в точке выполняется неравенство f(x1) < f(x0)(f(x1) > f(x0)), то точка x0 является максимумом (минимумом) функции.
То есть точкой, в которой функция будет принимать максимальное (минимальное) значение.
Точки, в которых функция принимает максимальное или минимальное значения, называются экстремумами функции.
В данном случае xmax, xmin - точки экстремума, а функция в данной точке называется экстремумом функции.
Точки, в которых производная функции равная нулю или не существует вовсе, называются критическими точками.
Если производная некоторой функции в точке равна нулю, а вторая производная отлична от нуля, то данная точка будет точкой максимума, если вторая производная меньше нуля, и минимума, если она больше нуля.
ОДЗ
Это одно из наиболее важных свойств функций, используемых в неравенствах, поскольку ОДЗ позволяет моментально, на первых этапах избавиться от возможных решений системы.
Использование монотонности функций при решении уравнений и неравенств основано на следующих теоретических фактах:
1. Строго монотонная функция принимает каждое свое значение ровно один раз.
2. Если одна функция возрастает, а другая убывает на одном и том же промежутке, то графики их, либо только один раз пересекутся, либо вообще не пересекутся, а это означает, что уравнение F(x)=G(x) имеет не более одного решения.
3. Если на некотором промежутке одна из функций убывает (возрастает), а другая принимает постоянные значения, то уравнение F(x)=G(x) либо имеет единственный корень, либо не имеет корней.
Пример 1.
Решите уравнение: x 3=2− x
Решение.
Рассмотрим функции f (x)= x 3 и g (x)=2− x.
Функция f(x) возрастает на всей области определения, а функция g(x) убывает на области определения. Следовательно, данное уравнение имеет не
более одного корня.
Подбором находим, что x=1.
Проверкой убеждаемся, что x=1 действительно корень уравнения.
Проверка: 13=2-1; 1=1.
Ответ: 1.