Бесконечные ряды и функции двух переменных
Бесконечные ряды
Важнейшим методом изучения функций является их разложение в бесконечные ряды. Использование бесконечных рядов по этой причине характерно как для математического анализа, так и для теорий, его развивающих.
В анализе рассматриваются как ряды с постоянными членами, так и функциональные ряды (например, степенные ряды, ряды Фурье, называемые также тригонометрическими рядами, и т.д.).
Перечислим некоторые причины, по которым так важна теория рядов.
1. Ряд является средством вычисления значений как элементарных, так и неэлементарных функций.
2. Ряды позволяют перенести определения функций из действительной области в область комплексных чисел, а так же в область абстрактных алгебраических величин, например, матриц.
Самый знаменитый пример – формула Эйлера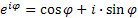 
. Действительно, 
.
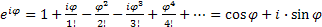3. Аналогия между функцией и вектором позволяет истолковать результаты математического анализа с точки зрения линейной алгебры, но в бесконечномерных пространствах. Это подход функционального анализа. Здесь разложение в ряд Тейлора трактуется как разложение произвольной функции в определенном базисе.
4. Ряды дают мощный вычислительный аппарат в теории дифференциальных уравнений.
Пример.
Решить уравнение y′′=y, y(0)=1, y′(0)=1. Пусть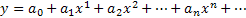 
, тогда 
.
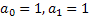Далее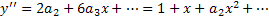 
. Отсюда 
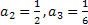. Продолжая подобным образом, получим, что 
.
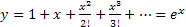5. Существует глубокая связь между бесконечными рядами и несобственными интегралами.
Оставив рассмотрение функциональных рядов до лекций, посвященных теории функций комплексного переменного и функциональному анализу, рассмотрим ряды с постоянными членами.
Пусть задана бесконечная последовательность чисел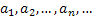 
. Составленный из этих чисел символический ряд 
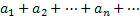называется бесконечным рядом, а сами числа членами ряда. Суммы вида 
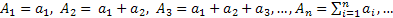называются частичными суммами.
Суммой ряда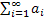 
называется конечный или бесконечный предел 
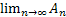. Если предел конечен, то ряд называется сходящимся, в противном случае расходящимся.
Примеры.
1. Ряд 1 – 2 + 3 – 4 + 5 –… является расходящимся, т.к. частичные суммы не имеют предела.
2. Ряд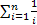 
расходится, как доказано ранее. Этот ряд называется гармоническим.
3. Ряд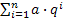 
сходится при 
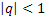к числу 
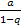, а при 
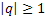расходится.
4. Ряд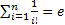 
, т. е. сходится.
Теорема 1. Остатками ряда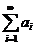 
называются ряды вида 
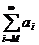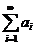. Ряд сходится тогда и только тогда, когда сходится любой из его остатков.
Теорема 2. Ряд, полученный умножением сходящегося ряда на число или суммированием двух сходящихся рядов, сходится.
Теорема 3. Общий член сходящегося ряда стремится к нулю (т. к. lim An-1 = lim An).
В теории рядов рассматриваются бесконечные ряды специального вида, например, положительные и знакопеременные.
Сходимость положительных рядов.
Теорема 4. Пусть даны ряды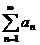 
и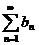 
. Если с некоторого места выполняется условие 
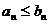, то из сходимости второго ряда вытекает сходимость первого. И наоборот, из расходимости первого ряда вытекает расходимость второго.
Теорема 5. Если существует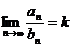 
, то выполняются условия предыдущей теоремы.
Действительно, с некоторого места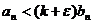 
.
Сравнивая произвольный ряд с рядом стандартным, например, геометрической прогрессией, можно получить признаки сходимости рядов.
Признак Коши. Если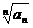 
стремится к числу q < 1, то ряд сходится.
Признак Даламбера. Если отношение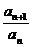 
стремится к числу q < 1, то ряд сходится. При q=1 необходимо особое исследование.