Важным направлением, обобщающим исходные идеи математического анализа, является рассмотрение функций нескольких переменных. Следует отметить, что без этого раздела анализа невозможно и исчерпывающее изложение методов функции одной переменной. В частности это относится к изучению неявных функций.
Рассмотрим множества 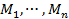 . Их прямым произведением
. Их прямым произведением  называется множество упорядоченных наборов по n элементов в каждом наборе
называется множество упорядоченных наборов по n элементов в каждом наборе 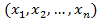 , где
, где 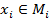 говорят, что на подмножестве M прямого произведения
говорят, что на подмножестве M прямого произведения  задана функция от n переменных, если каждому набору
задана функция от n переменных, если каждому набору 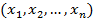 соответствует единственное значение y из области значений Y.
соответствует единственное значение y из области значений Y.
В частности функция от двух переменных определена на множестве пар 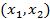 . Часто в этом случае независимые переменные обозначают через x и y, а зависимую через z. Изучение функции от двух переменных естественным образом увязывается с декартовой системой координат в трехмерном пространстве. Роль графика функции z = F(x,y) играет некоторая поверхность, образованная точками с координатами (x, y, F(x,y)).
. Часто в этом случае независимые переменные обозначают через x и y, а зависимую через z. Изучение функции от двух переменных естественным образом увязывается с декартовой системой координат в трехмерном пространстве. Роль графика функции z = F(x,y) играет некоторая поверхность, образованная точками с координатами (x, y, F(x,y)).
На функции нескольких переменных переносятся такие понятия как область определения, область значений, непрерывность. Функция называется непрерывной, если бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции. В случае функции нескольких переменных бесконечно малым приращениям аргументов должно соответствовать бесконечно малое приращение функции. Для функции двух переменных z = F(x,y) приращения аргументов 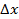 и
и 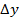 дают приращение функции
дают приращение функции 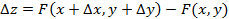 . Пусть
. Пусть 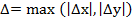 , тогда функция z непрерывна в точке (x,y), если
, тогда функция z непрерывна в точке (x,y), если 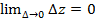 .
.
Понятие предела распространяется на функции нескольких переменных без каких-либо проблем.
В случае, если мы зафиксируем один из аргументов функции двух переменных, мы получим функцию одного переменного:
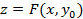 , где
, где 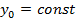 .
.
Допустим, что эта функция дифференцируема в точке 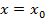 , тогда ее производная
, тогда ее производная
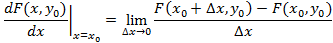
называется частной производной по x и обозначается через 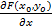 или
или 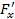 . Аналогично вводится и частная производная по y –
. Аналогично вводится и частная производная по y – 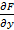 . Для функций более чем двух переменных также легко определяются частные производные по различным переменным.
. Для функций более чем двух переменных также легко определяются частные производные по различным переменным.
Можно легко придумать функции, имеющие частные производные в точке, но даже не непрерывные в ней. Чтобы функция была «хорошей», желательно потребовать от нее существование частных производных в окрестности точки. Тогда, образно говоря, ткань функции-поверхности соткана из двух семейств гладких нитей, идущих вдоль осей x и y.
Выражение 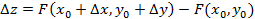 называется полным приращением функции z = F(x,y).
называется полным приращением функции z = F(x,y).
Теорема.
Если частные производные 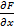 и
и 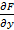 существуют и непрерывны в некоторой окрестности точки
существуют и непрерывны в некоторой окрестности точки 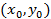 , то имеет место формула
, то имеет место формула 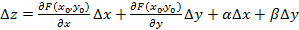 , где
, где 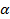 и
и 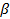 зависят от
зависят от 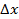 и
и 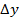 и вместе с ними стремятся к нулю.
и вместе с ними стремятся к нулю.
Доказательство.
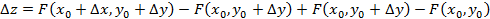
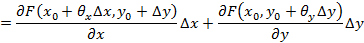
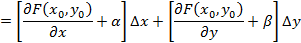
Полным дифференциалом функции двух переменных называется линейная часть приращения функции: 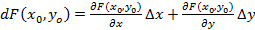 .
.
Касательная плоскость к поверхности z = F(x,y).
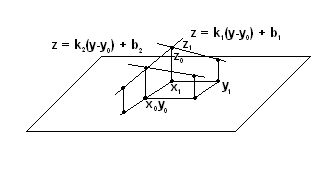 Пусть через точку
Пусть через точку 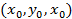 проходят две прямые:
проходят две прямые: 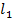 в плоскости, параллельной XOZ, с уравнением
в плоскости, параллельной XOZ, с уравнением 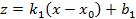 и
и 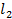 в плоскости, параллельной YOZ, с уравнением
в плоскости, параллельной YOZ, с уравнением 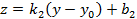 . Уточним уравнение первой прямой:
. Уточним уравнение первой прямой: 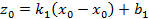 , откуда
, откуда 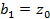 . Точно так же уравнение второй прямой
. Точно так же уравнение второй прямой 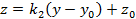 Если прямую
Если прямую 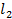 заставить скользить параллельно себе по прямой
заставить скользить параллельно себе по прямой 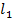 , то она заметёт плоскость. Установим, каково её уравнение. Пусть мы выбрали на
, то она заметёт плоскость. Установим, каково её уравнение. Пусть мы выбрали на 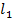 точку, соответствующую координате
точку, соответствующую координате 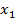 , тогда
, тогда 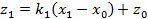 . Прямая, параллельная
. Прямая, параллельная 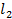 , имеет уравнение
, имеет уравнение 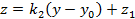 или
или 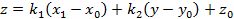 . Переобозначим
. Переобозначим 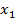 через x и получим уравнение плоскости
через x и получим уравнение плоскости 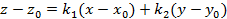 .
.
Из приведённых рассуждений следует, что уравнение касательной плоскости имеет вид:
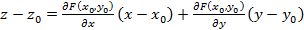
Сравнение этого уравнения с формулой для полного дифференциала даёт геометрический смысл этой формулы: 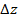 – полное приращение при движении по поверхности, dz – полное приращение при движении по плоскости.
– полное приращение при движении по поверхности, dz – полное приращение при движении по плоскости.
По аналогии с функциями одной переменной можно определить частные производные высших порядков. Так для функции от двух переменных теоретически существует четыре производных второго порядка
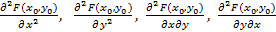
Оказывается, что третья и четвёртая производные второго порядка, называемые смешанными частными производными при некоторых условиях оказываются равными.
Пример.
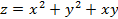
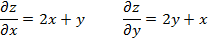
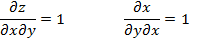
 Теорема. Пусть в некоторой окрестности точки (x0, y0) определена функция Z = F(x, y), имеющая в этой области непрерывные первые частные производные, а так же смешанные вторые частные производные. Тогда эти смешанные производные равны между собой в точке (x0, y0).
Теорема. Пусть в некоторой окрестности точки (x0, y0) определена функция Z = F(x, y), имеющая в этой области непрерывные первые частные производные, а так же смешанные вторые частные производные. Тогда эти смешанные производные равны между собой в точке (x0, y0).
Доказательство.
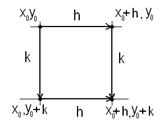
Рассмотрим выражение
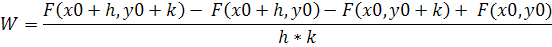 .
.
Его можно свернуть двумя путями:
1. 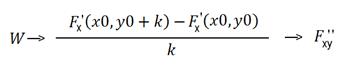
2. 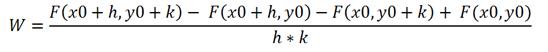
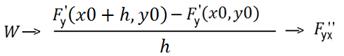
Откуда и следует теорема о смешанных производных.
Формула Тейлора.
Для функции двух переменных имеет место формула аналогичная формуле Тейлора, хотя она значительно сложнее.
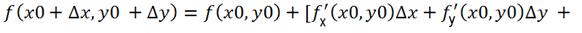
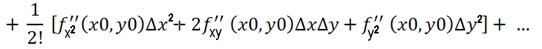
Экстремумы функции двух переменных.
Поскольку частная производная указывает рост по направлению изменения одной из независимых переменных, для точек экстремума частные производные должны обращаться в ноль. Однако это и в случае функции одной переменной не гарантирует наличие экстремума. Тем более нет гарантии для функции двух переменных.
Если f′x и f′y равны нулю, поведение функции определяется членами ряда Тейлора 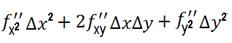 то есть речь идет об изучении поверхности Z = a11x2 + 2a12xy + a22y2.
то есть речь идет об изучении поверхности Z = a11x2 + 2a12xy + a22y2.
Выделим полный квадрат, предварительно умножив выражение на a11:
а211 x2 + 2 a11 a12xy + а212 y2 – а12 y2 + a11 a22 y2 = (a11x + a12 y)2 + (a11 a22 – а212) y2
Первый член всегда положителен. Если a11 a22 – а212 > 0, то и вся сумма положительна, но обращается в ноль. Значит, мы имеем максимум при a11 < 0 или минимум при a11 > 0. Если же a11 a22 – а212 < 0, то можно так подобрать x и y, что выражение примет разные знаки. Экстремума нет.