Элементы теории функции комплексного переменного.
Комплексные числа.
Комплексным числом α называется пара действительных чисел a и b, взятых в определённом порядке: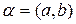 
.
Рассмотрим число, изображаемой парой (0;1) – его обозначим через i. Тогда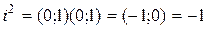 
, 
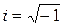, всякое комплексное число может быть записано в виде:
 | |||
 |
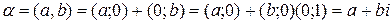
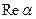
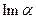
Очевидно, что если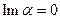 
, то комплексное число 
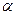обращается в действительное число, если 
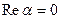, в чисто мнимое. Два комплексных числа, по определению, называются равными, если равны между собой их действительные части и равны их мнимые.
Два комплексных числа имеющих одну и ту же первую компоненту, но противоположные по знаку вторые компоненты, называются сопряжёнными и обозначаются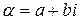 
, 
.
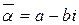Всякое комплексное число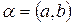 
мы можем изображать на плоскости с координатами a и b.
y
α
b
0 a x
Ось абсцисс называется действительной осью, ось ординат – мнимой осью. Плоскость, точки которой изображают комплексные числа, называют комплексно-числовой плоскостью.
Модулем комплексного числа α называют положительное число r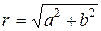 
и обозначают через 
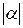. Направление вектора α определяется с помощью угла j положительным направлением оси Ox и направлением этого вектора 
j изображает угол на который нужно повернуть «+» направление оси Ox, чтобы совпало с направлением вектора α. Это число j называется аргументом комплексного числа α и обозначается через 
. Очевидно, что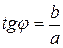 
, так как r и j являются полярными координатами точки 
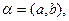то имеем: 
, 
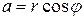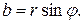
Формы записи комплексного числа
1) z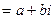 
- алгебраическая форма комплексного числа.
2)z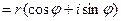 
- тригонометрическая форма комплексного числа,
3) z=reiφ или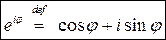 
-экспоненциальная запись комплексного числа(формула Эйлера)
Арифметические действия над комплексными числами
Сложение (вычитание) комплексных чисел:
z 1 ± z 2 = (x 1 + iy 1) ± (x 2 + iy 2) = (x 1 ± x 2) + i (y 1 ± y 2),
то есть при сложении (вычитании) комплексных чисел складываются (вычитаются) их действительные и их мнимые части.
Например,
1) (1 + i) + (2 – 3 i) = 1 + i + 2 –3 i = 3 – 2 i;
2) (1 + 2 i) – (2 – 5 i) = 1 + 2 i – 2 + 5 i = –1 + 7 i.
Основные свойства сложения комплексных чисел:
1) z 1 + z 2 = z 2 + z 1 — коммутативность;
2) z 1 + z 2 + z 3 = (z 1 + z 2) + z 3 = z 1 + (z 2 + z 3) — ассоциативность;
3) z 1 – z 2 = z 1 + (– z 2) — обратная операция (вычитание);
4) z + (– z) = 0 — сложение противоположных чисел;
5) 
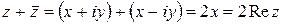— сложение комплексно сопряженных чисел.
Умножение комплексных чисел в алгебраической форме:
z 1∙ z 2 = (x 1 + iy 1)∙(x 2 + iy 2) = x 1 x 2 + x 1 iy 2 + iy 1 x 2 + i 2 y 1 y 2 = (x 1 x 2 – y 1 y 2) + i (x 1 y 2 + y 1 x 2),
то есть умножение комплексных чисел в алгебраической форме проводится по правилу алгебраического умножения двучлена на двучлен с последующей заменой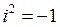 
и приведением подобных по действительным и мнимым слагаемым.
Например,
1) (1 + i)∙(2 – 3 i) = 2 – 3 i + 2 i – 3 i 2 = 2 – 3 i + 2 i + 3 = 5 – i;
2) (1 + 4 i)∙(1 – 4 i) = 1 – 42 i 2 = 1 + 16 = 17;
3) (2 + i)2 = 22 + 4 i + i 2 = 3 + 4 i.
Умножение комплексных чисел тригонометрической форме:
z 1∙ z 2 = r 1(cos j 1 + i sin j 1)× r 2(cos j 2 + i sin j 2) =
= r 1 r 2(cos j 1cos j 2 + i cos j 1sin j 2 + i sin j 1cos j 2 + i 2 sin j 1sin j 2) =
= r 1 r 2((cos j 1cos j 2 – sin j 1sin j 2) + i (cos j 1sin j 2 + sin j 1cos j 2))
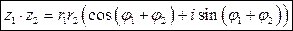Произведение комплексных чисел в тригонометрической форме
то есть при умножении комплексных чисел в тригонометрической форме их модули перемножаются, а аргументы складываются.
Например,
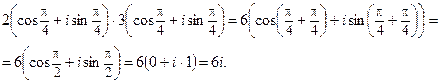
Основные свойства умножения комплексных чисел :
1) z 1× z 2 = z 2× z 1 — коммутативность;
2) z 1× z 2× z 3 = (z 1× z 2)× z 3 = z 1×(z 2× z 3) — ассоциативность;
3) z 1×(z 2 + z 3) = z 1× z 2 + z 1× z 3 — дистрибутивность относительно сложения;
4) z ×0 = 0; z ×1 = z; — умножение на ноль и на единицу;
5) 
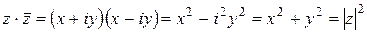— умножение комплексно сопряженных чисел.
Деление комплексных чисел — это обратная умножению операция, поэтому если z×z 2 = z 1 и z 2 ¹ 0, то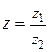 
.
При выполнении деления в алгебраической форме числитель и знаменатель дроби умножаются на число, комплексно сопряженное знаменателю:
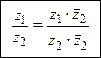Деление комплексных чисел в алгебраической форме.
При выполнении деления комплексных чисел в тригонометрической форме их модули делятся, а аргументы вычитаются:
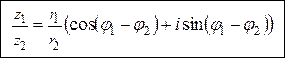Деление комплексных чисел в тригонометрической форме.
Например,
1) 
;
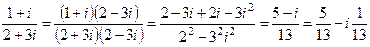2) 
.
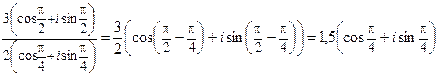Возведение комплексного числа в натуральную степень :
возведение комплексного числа в натуральную степень удобнее выполнять в тригонометрической форме:
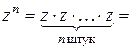
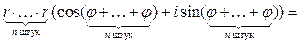
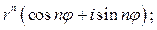
в результате получается формула Муавра:
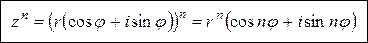Формула Муавра,
то есть при возведении комплексного числа в натуральную степень его модуль возводится в эту степень, а аргумент умножается на показатель степени.
Пример (возведение комплексного числа в натуральную степень)
Вычислим (1 + i)10:
