МЕТОД КОНЕЧНЫХ ЭЛЕМЕНТОВ
В РАСЧЕТЕ КОНСТРУКЦИЙ
НА УПРУГОМ ОСНОВАНИИ
Общие принципы расчета на действие внешней нагрузки
Матрица жесткости произвольного
Конечного элемента
 (1)
(1)
Z (x, y, z) = F (x, y, z) f s, (2)
Z g = A f s (3)
f s = A -1 Z g (4)
σ = Cε (5)
ε = ε (x, y, z) = B (x, y, z) f s = B f s (6)
При 
 , (7)
, (7)
 . (8)
. (8)
Z 0 g = L (x, y, z) f s = L f s (9)
 (10)
(10)
R 0 g = k с Z 01 g (11)
 (12)
(12)
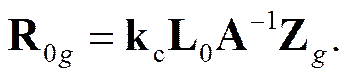 (13)
(13)
 (14)
(14)
 (15)
(15)
 (16)
(16)
Из T 1 – T 2 = U:
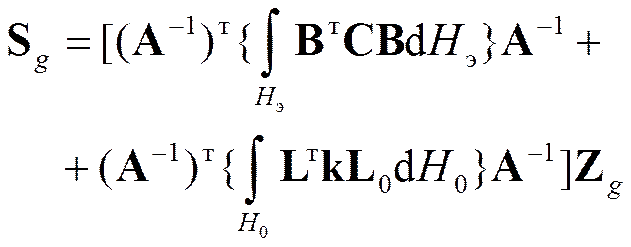 (17)
(17)
 (18)
(18)
 (19)
(19)
 (20)
(20)
 (21)
(21)
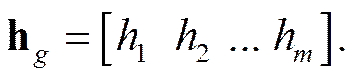 (22)
(22)
 . (23)
. (23)
Общий ход расчета методом перемещений
1.  (24)
(24)
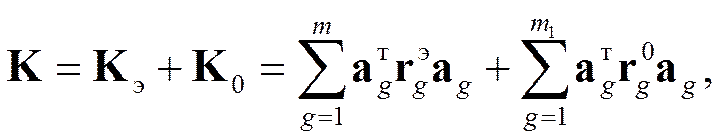 (25)
(25)
2. Возможная работа узловых сил
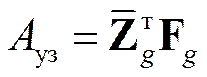 , где
, где 
 ,
,
Так как 
то из условия А уз= Aq получим
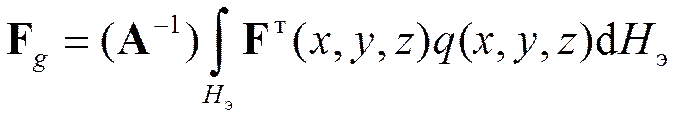 (26)
(26)
3. KZ + R = 0 (27)
4. S g у = rg a g Z (28)
S g = S g у + S 0= rg a g Z + S 0(29 )
5.  (30)
(30)
6.  (31)
(31)
Рамы и балки
На упругом основании
Общие положения



– на осадку
 (32)
(32)
– на сдвиг
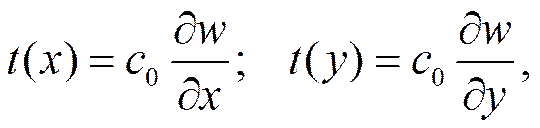 (33)
(33)

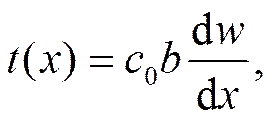 (34)
(34)
Матрицы жесткости конечных
Элементов
КЭ с четырьмя степенями свободы

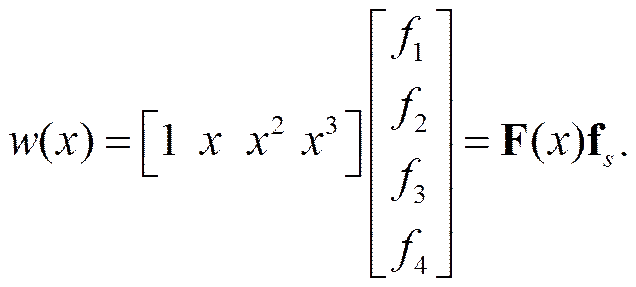 (35)
(35)
 (36)
(36)

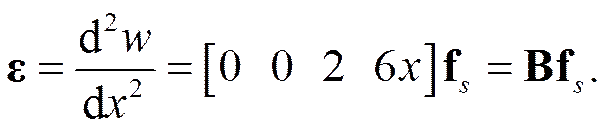 (37)
(37)
Тогда  (38)
(38)
 (39)
(39)
 (40)
(40)

Тогда  (41)
(41)
Реакции упругого основания
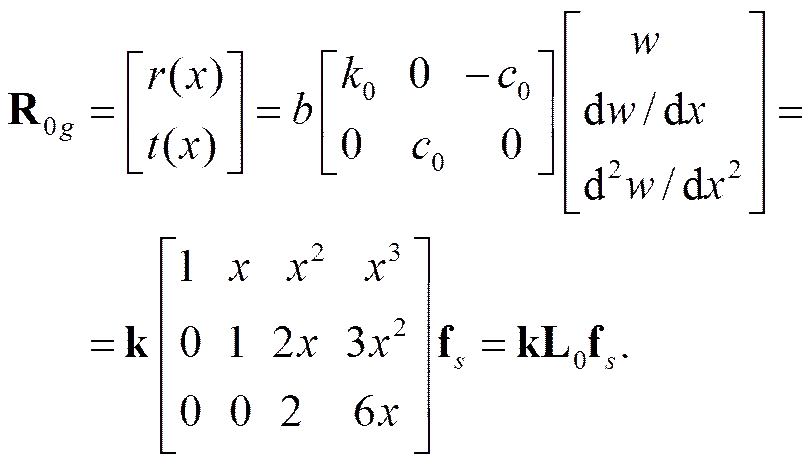 (42)
(42)
 (43)
(43)
 (44)
(44)
 (45)
(45)
КЭ с тремя степенями свободы

 (46)
(46)
 (47)
(47)






Тогда
 (48)
(48)
 (49)
(49)
 (50)
(50)
Рациональный размер конечного элемента

где 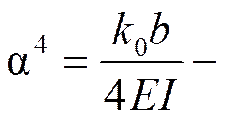 - линейная характеристика балки на упругом основании
- линейная характеристика балки на упругом основании
Учет односторонней связи с основанием
КЭ с четырьмя степенями свободы




 (51)
(51)
КЭ с тремя степенями свободы



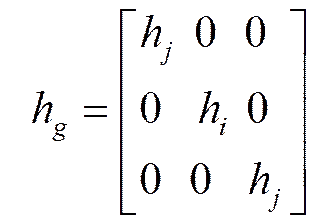 (52)
(52)
Общий алгоритм расчета
–без учета односторонней связи
 (53)
(53)
–с учетом односторонней связи
 (54)
(54)
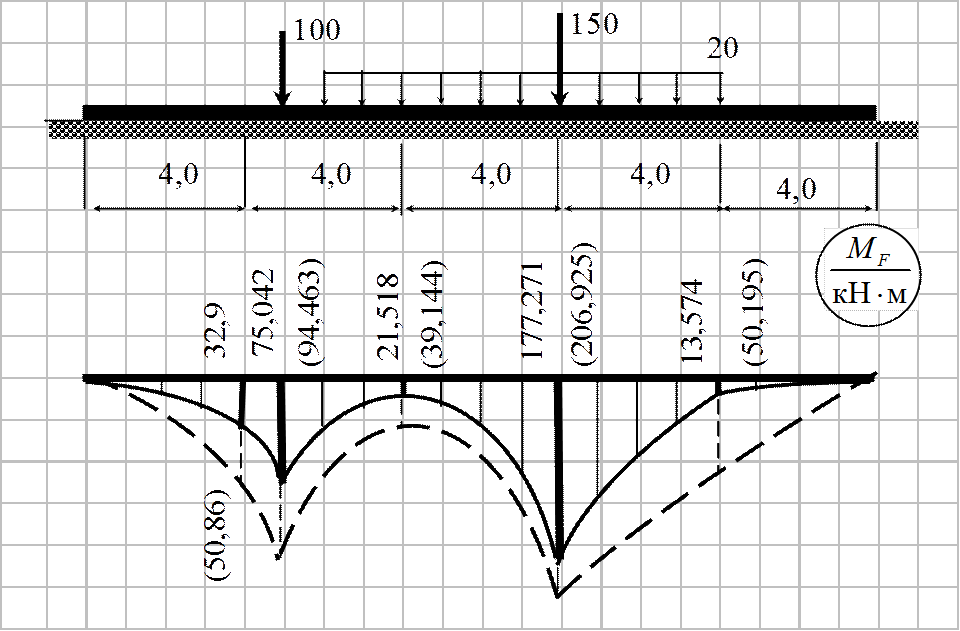
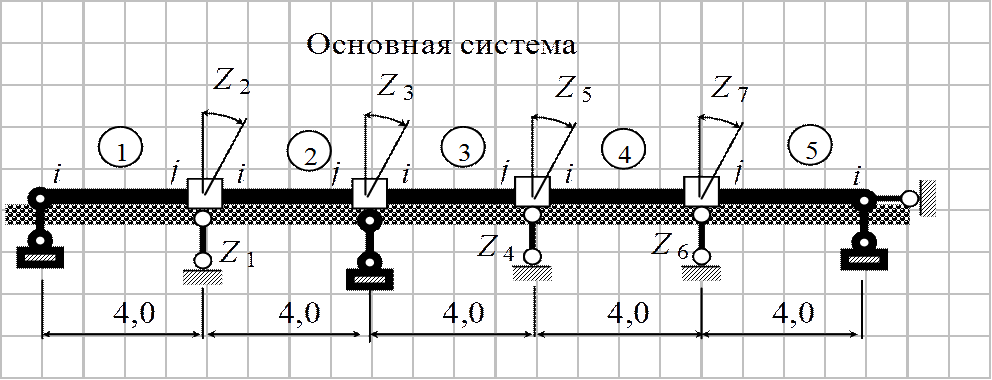
Пример 1.

k 0 = 32000 кН/м3; b = 1,25 м; EI = 2,56∙106 кН∙м2
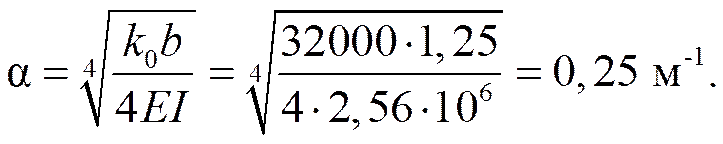
Принимаем длину конечных элементов l =4,0 м. Тогда величина α l = 0,25∙4 = 1

1. Исходные матрицы



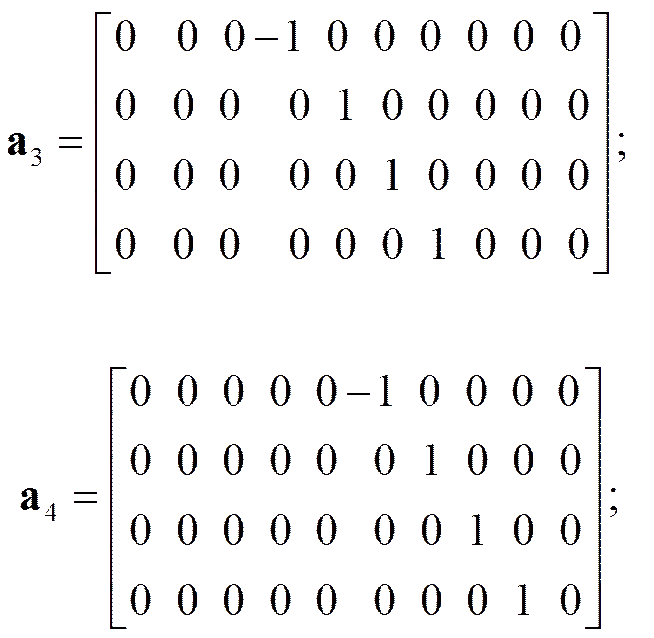


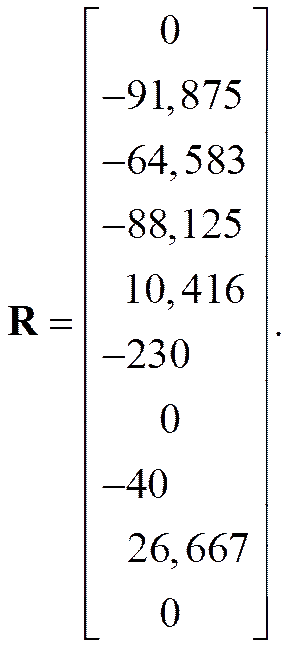
2. Решение 

3. Определим усилия в сечении k второго КЭ в точке приложения силы F =100 кН.

Реакция упругого основания
r (x) = k 0∙ b ∙ w = 19,172 +5,38 x – 0,486 x 2 + 0,028 x 3.


4. Учет односторонней связи балки с упругим основанием.




r (x) = k 0∙ b ∙ w = 14,136 +7,332– 0,639 x 2 + 0,0295 x 3.





Преобразованные матрицы жесткости




Пример 2.

k 0 = 26000 кН/м3; b = 1,0 м; EI = 0,2∙106 кН∙м2.

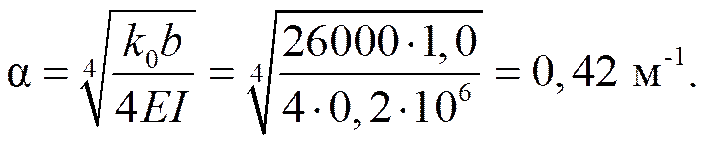
Принимаем размер КЭ l = 2,0 м.
Тогда величина α l = 0,42∙2 = 0,84 находится в допустимых пределах
1. Исходные матрицы.








2. Решение


3. Экстремальное значение изгибающего момента в пределах элемента 4.


откуда x = 0,129 м.
Тогда


Прямоугольные плиты на упругом основании
Общие положения и составление системы разрешающих
Уравнений
Железобетонные плиты на упругом основании являются одним из наиболее важных конструктивных элементов промышленного, гражданского, гидротехнического и дорожного строительства, и поэтому необходимость наиболее точно отразить их напряженно – деформированное состояние является важной задачей теории сооружений.
В данном разделе рассмотрим расчет тонких плит, для которых справедливы гипотезы Кирхгофа-Лява. Материал плит считается идеально упругим и ортотропным.
При использовании МКЭ прямоугольная плита разбивается на ряд прямоугольных КЭ (рис. 8.12, а), соединенных между собой в узлах. При использовании метода перемещений в каждый узел полученной дискретной расчетной схемы вводятся дополнительные связи, припятствующие смещениям в трех направлениях: углам поворота в направлении координатных осей и вертикальному перемещению перпендикулярно срединной поверхности плиты (рис. 8.12, б). Углом поворота в плоскости плиты пренебрегают. Следовательно, состояние любого узла n КЭ (рис. 8.13) может быть характеризовано тремя узловыми силами и темя перемещениями:
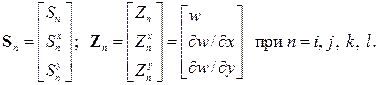 (8.57)
(8.57)
Таким образом, матрица жесткости такого элемента будет 12-го порядка, и ее удобно представить в блочной форме:
 (8.58)
(8.58)
или в краткой форме для КЭ
Sg = r g Z g. (8.59)
Представление матрицы жесткости в блочной форме позволяет отказаться от использования единого матричного алгоритма при составлении системы разрешающих уравнений. Использование матричного алгоритма не всегда удобно, так как матрицы преобразования деформаций, входящие в выражение (8.31), содержат большое число нулей (см. примеры 8.2 и 8.3), что излишне загромождает память ЭВМ при их использовании. Поэтому при составлении системы уравнений метода перемещений удобнее использовать блочный принцип.
Предположим, что все перемещения находятся в единой системе координат, которая в общем случае может не совпадать с направлениями координатных осей, принятых для отдельных элементов. Обозначим перемещения узлов и узловых сил в общей системе координат как Z n * и S n *. Для плит эти матрицы будут трехмерными [см. (8.57)]. Чтобы перейти к составлению матрицы K (8.27), для каждого элемента вводятся матрицы преобразования координат, с помощью которых матрицы Z n и S n заменяются матрицами Z n * и S n *. Например, для узла i S i = a i S i *, Z i = a i Z i *. В случае совпадения единой системы координат с системами координат отдельных элементов матрицы преобразования координат будут единичными.
Значения Z n и S n, выраженные через Z n * и S n *, подставляются в в (8.58), например, для первой строки:

или после умножения слева на  ,
,
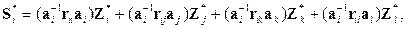 (8.60)
(8.60)
где выражения в скобках являются блоками матрицы K, составляемой для общей системы координат.
Рассмотрим часть области плиты, поделенной на прямоугольные конечные элементы (рис. 8.14), и составим уравнение равновесия для узла n:
 (8.61)
(8.61)
где R n – матрица свободных членов для узла n.
Подставив выражения для S * на основании (8.60) в (8.61), получим:
 (8.62)
(8.62)
На основании совместности деформаций в узлах дискретной схемы плиты для узла n (см. рис. 8.14)
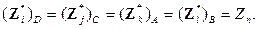 (8.63)
(8.63)
Подставив (8.63) в (8.62) получим:
 (8.64)
(8.64)
где выражения в круглых скобках
 (8.65)
(8.65)
Уравнения типа (8.64) составляются для каждого узла: результатом объединения этих уравнений является выражение (8.27).
При совпадении местных систем координат, принятых для каждого отдельного элемента, с общей системой матрицы преобразования координат будут единичными и тогда  В этом случае блоки матриц жесткости можно сразу (без преобразования) из (8.58) подставлять в (8.64).
В этом случае блоки матриц жесткости можно сразу (без преобразования) из (8.58) подставлять в (8.64).
Граничные условия для расчетной схемы учитываются при составлении блоков матриц усилий и перемещений (см. 8.57), определяемых для каждого граничного элемента.
Матрица жесткости прямоугольного элемента плиты
Для выражения поверхности прогиба примем бикубический полином, удовлетворяющий однородному дифференциальному уравнению изгибаемой плиты при отсутствии упругого основания:
 (8.66)
(8.66)
Полином (8.66) используется почти во всех работах, посвященных расчету тонких плит МКЭ. Это объясняется тем, что он дает достаточно точные результаты, особенно при решении задач прочности, хотя и допускает разрыв деформаций в углах поворота между смежными элементами.
Выражения для прогибов и углов поворота согласно (8.57) примут вид:
 (8.67)
(8.67)
Подставив в матрицу L (8.67) координаты узлов конечного элемента (см. рис. 8.13), получим матрицу А коэффициентов при f s (8.3). Обращение этой матрицы дает A -1 (табл. 8.1):
Таблица 8.1
Матрица параметров fs для прямоугольного КЭ
| A-1 | = | ||||||||||||
| –3/ a 2 | –2/ a | 3/ a 2 | –1/ a | ||||||||||
| –3/ b 2 | –2/ b | 3/ b 2 | –1/ b | ||||||||||
| –1/ ab | –1/ b | –1/ a | 1/ ab | 1/ a | –1/ ab | 1/ ab | 1/ b | ||||||
| 3/ a 2 b | 2/ ab | –3/ a 2 b | 1/ ab | 3/ a 2 b | –1/ ab | –3/ a 2 b | –2/ ab | ||||||
| 3/ ab 2 | 2/ ab | –3/ ab 2 | –2/ ab | 3/ ab 2 | –1/ ab | –3/ ab 2 | 1/ ab | ||||||
| 2/ a 3 | 1/ a 2 | –2/ a 3 | 1/ a 2 | ||||||||||
| 2/ b 3 | 1/ b 2 | –2/ b 3 | 1/ b 2 | ||||||||||
| –2/ a 3 b | –1/ a 2 b | 2/ a 3 b | –1/ a 2 b | –2/ a 3 b | 1/ a 2 b | 2/ a 3 b | 1/ a 2 b | ||||||
| –2/ ab 3 | –1/ ab 2 | 2/ ab 3 | 1/ ab 2 | –2/ ab 3 | 1/ ab 2 | 2/ ab 3 | –1/ ab 2 |
Выражения для вторых производных от w получим из (8.67):
 (8.68)
(8.68)
Матрица жесткости С (8.5) для бесконечного малого элемента в случае изгиба тонких ортотропных плит дает соотношения между изгибающими моментами и деформациями плиты:
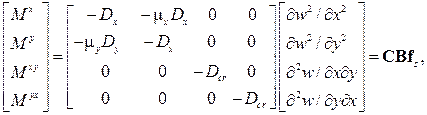 (8.69)
(8.69)
где Dx = Exh 3/(12ν) – изгибная жесткость плиты в направлении оси x;
Dy = Eyh 3/(12ν) – изгибная жесткость плиты в направлении оси y;
Dk = Gh 3/6 – жесткость при кручении; μ xDx = μ yDy = D μ; ν = 1– μ x μ y.
На основании принятой модели упругого основания [см. (8.32) и (8.33)] реакции упругого основания в матричной форме имеют вид:
 (8.70)
(8.70)
где
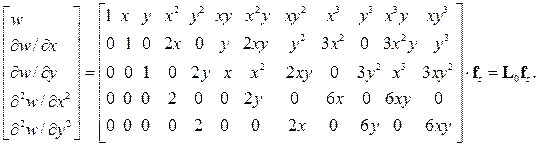 (8.71)
(8.71)
Подставляя матрицы L (8.67), A -1 (табл. 8.1), В (8.68), С (8.69), k (8.70) и L 0 (8.71) в выражения (8.19) и (8.20) и интегрируя в пределах от 0 до а в направлении оси x и от 0 до b в направлении оси y, получим в общем виде:  –матрицу жесткости собственно конечного элемента, учитывающую его упругие свойства;
–матрицу жесткости собственно конечного элемента, учитывающую его упругие свойства;  – матрицу, учитывающую свойства упругого основания.
– матрицу, учитывающую свойства упругого основания.
Матрица  представлена в виде суммы трех матриц:
представлена в виде суммы трех матриц:  , где
, где  зависит от коэффициента k 0, а
зависит от коэффициента k 0, а  и
и  – от коэффициента с 0 по направлениям координатных осей. При
– от коэффициента с 0 по направлениям координатных осей. При  =0 получаем наиболее распространенную и простую модель упругого основании – модель Винклера. При отсутствии упругого основания
=0 получаем наиболее распространенную и простую модель упругого основании – модель Винклера. При отсутствии упругого основания  = 0. Матрицы жесткости
= 0. Матрицы жесткости  ,
,  ,
,  и
и  приведены, соответственно, в таблицах 8.2, 8.3, 8.4 и 8.5.
приведены, соответственно, в таблицах 8.2, 8.3, 8.4 и 8.5.
Распределенные (погонные) усилия при расчете плиты определяются по выражению (8.30), которое в данном случае удобно записать в виде  . Матрица
. Матрица  приведена в таблице 8.6. В эту матрицу подставляются координаты узлов для изгибающих моментов и координаты середины элемента – для крутящего момента. Размер матрицы
приведена в таблице 8.6. В эту матрицу подставляются координаты узлов для изгибающих моментов и координаты середины элемента – для крутящего момента. Размер матрицы  – (9 х 12).
– (9 х 12).
Таблица 8.2
Матрица жесткости  прямоугольного КЭ плиты
прямоугольного КЭ плиты
| Si | = | r 11 | r 12 | r 13 | r 14 | r 15 | r 16 | r 17 | r 18 | r 19 | r 1,10 | r 1,11 | r 1,12 | Zi | |
| r 22 | r 23 | – r 15 | r 25 | – r 18 | r 28 | r 1,11 | r 2,11 | 
| ||||||

| r 33 | r 16 | r 36 | – r 19 | r 39 | – r 1,12 | r 3,12 | 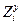
| |||||||
| Sj | r 11 | – r 12 | r 13 | r 1,10 | – r 1,11 | r 1,12 | r 17 | – r 18 | r 19 | Zj | |||||

| r 22 | – r 23 | – r 1,11 | r 2,11 | r 18 | r 28 | 
| ||||||||

| r 33 | – r 1,12 | r 3,12 | – r 19 | r 39 | 
| |||||||||
| Sk | r 11 | – r 12 | – r 13 | r 14 | – r 15 | – r 16 | Zk | ||||||||

| r 22 | r 23 | r 15 | r 25 | 
| ||||||||||

| Симметрично | r 33 | – r 16 | r 36 | 
| ||||||||||
| Sl | r 11 | r 12 | –r 13 | Zl | |||||||||||

| r 22 | – r 23 | 
| ||||||||||||

| r 33 | 
|
В таблице 8.2: 

Таблица 8.3
Матрица жесткости 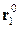 прямоугольного КЭ плиты
прямоугольного КЭ плиты
| 461 a | 461 ma | – 274 a | 199 ma | – 116 a | – 116 ma | 199 a | – 274 a | ||||
| 80 a 2 | 80 ma 2 | 274 a | – 60 a 2 | 42 ma 2 | 116 a | – 30 a 2 | – 28 ma 2 | 199 a | 40 a 2 | – 42 ma 2 | |
| 80 m 2 a 2 | 199 ma | – 42 ma 2 | 40 m 2 a 2 | 116 ma | – 28 ma 2 | – 30 m 2 a 2 | 274 ma | 42 ma 2 | – 60 m 2 a 2 | ||
| – 461 a | 461 ma | – 199 a | – 274 ma | 116 a | – 116 ma | ||||||
| 80 a 2 | – 63 ma 2 | – 199 a | 40 a 2 | 42 ma 2 | – 116 a | – 30 a 2 | 28 ma 2 | ||||
| 80 m 2 a 2 | 274 ma | – 42 ma 2 | – 60 m 2 a 2 | 116 ma | 28 ma 2 | – 30 m 2 a 2 | |||||
| Симметрично | – 461 a | – 461 ma | 274 a | – 199 ma | |||||||
Общий множитель 
| 80 a 2 | 63 ma 2 | – 274 a | – 60 a 2 | 42 ma 2 | ||||||
| 80 m 2 a 2 | – 199 ma | – 42 ma 2 | 40 m 2 a 2 | ||||||||
| 461 a | – 461 ma | ||||||||||
| 80 a 2 | – 63 ma 2 | ||||||||||
| 80 m 2 a 2 |
Таблица 8.4
Матрица жесткости  прямоугольного КЭ плиты
прямоугольного КЭ плиты
| 1266 m | 609 b | 381 mb | – 1266 m | 189 b | – 381 mb | 384 m | – 63 b | 39 mb | – 384 m | – 433 b | –39 mb |
| 532 b 2/ m | 210 b 2 | – 609 b | 77 b 2/ m | – 210 b 2 | 433 b | – 119 b 2/ m | – 433 b | – 364 b 2/ m | |||
| 12 mb 2 | – 381 mb | 105 b 2 | –12 mb 2 | 276 mb | – 105 b 2 | 9 mb 2 | – 276 mb | – 210 b 2 | – 9 mb 2 | ||
| 1266 m | – 189 b | 381 mb | – 384 m | 63 b | –39 mb | 384 m | 433 b | 39 mb | |||
| 112 b 2/ m | – 105 b 2 | 63 b | 56 b 2/ m | – 63 b | – 119 b 2/ m | ||||||
| 12 mb 2 | – 276 mb | 105 b 2 | – 9 mb 2 | 276 mb | 210 b 2 | 9 mb 2 | |||||
| Симметрично | 1266 m | – 189 b | – 66 mb | –1266 m | – 609 b | 66 mb | |||||
Общий множитель 
| 112 b 2/ m | 231 b | 77 b 2/ m | ||||||||
| 12 mb 2 | 66 mb | –12 mb 2 | |||||||||
| 1266 m | 609 b | – 66 mb | |||||||||
| 532 b 2/ m | |||||||||||
| 12 mb 2 |
Таблица 8.5
Матрица жесткости 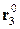 прямоугольного КЭ плиты
прямоугольного КЭ плиты
| 636/ m | 66 a/m | 84 a | 246/ m | – 39 a/m | 42 a | – 246/ m | 39 a/m | 42 a | – 636/ m | – 66 a/m | 84 a |
| 12 a 2/ m | 39 a/m | – 9 a 2/ m | – 39 a/m | 9 a 2/ m | – 66 a/m | – 12 a 2/ m | |||||
| 112 ma 2 | 42 a | 56 ma 2 | – 42 a | – 14 ma 2 | – 84 a | – 28 ma 2 | |||||
| 636/ m | – 69 a/m | 84 a | – 636/ m | 66 a/m | 84 a | – 246/ m | – 39 a/m | 42 a | |||
| 12 a 2/ m | 66 a/m | –12 a 2/ m | 39 a/m | 9 a 2/ m | |||||||
| 112 ma 2 | – 84 a | – 28 ma 2 | – 42 a | – 14 ma 2 | |||||||
| Симметрично | 636/ m | – 66 a/m | – 84 a | 246/ m | 39 a/m | – 42 a | |||||
Общий множитель 
| 12 a 2/ m | – 39 a/m | –9 a 2/ m | ||||||||
| 112 ma 2 | – 42 a | 56 ma 2 | |||||||||
| 636/ m | 66 a/m | – 84 a | |||||||||
| 12 a 2/ m | |||||||||||
| 112 ma 2 |
Таблица 8.6
Матрица усилий  прямоугольного КЭ плиты
прямоугольного КЭ плиты
| Zi | |||||||||||||||

| Dx μ | 2 Dxa | 2 D μ b | –3 Dxa/a | Dxa | –3 D μ b /b | D μ b | 
| |||||||
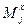
| –3 Dxa/a | – Dxa | Dx μ | –2 Dxa | 2 D μ b | –3 D μ b /b | D μ b | 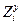
| |||||||

| –3 D μ b /b | – D μ b | Dx μ | –2 Dxa | –2 D μ b | –3 Dxa/a | – Dxa | Zj | |||||||

| –3 D μ b /b | – D μ b | –3 Dxa/a | Dxa | Dx μ | 2 Dxa | –2 D μ b | 
| |||||||

| = | Dy μ | 2 D μ a | 2 Dyb | –3 D μ a /a | D μ a | –3 Dyb/b | Dyb | 
| ||||||

| –3 D μ a /a | – D μ a | Dy μ | –2 D μ a | 2 Dyb | –3 Dyb/b | Dyb | Zk | |||||||

| –3 Dyb/b | – Dyb | Dy μ | –2 D μ a | –2 Dyb | –3 D μ a /a | – D μ a | 
| |||||||

| –3 Dyb/b | – Dyb | –3 D μ a /a | D μ a | Dy μ | 2 D μ a | –2 Dyb | 
| |||||||
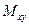
| –8 Dka/b | – Dkb | – Dka | 8 Dka/b | – Dkb | Dka | –8 Dka/b | Dkb | Dka | 8 Dka/b | Dkb | – Dka | Zl | ||

| |||||||||||||||
| В таблице 8.6: | 
|
