Как известно, далеко не всякое алгебраическое уравнение
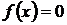
может быть решено аналитически. Это относится к большинству трансцендентных уравнений и к алгебраическим уравнениям выше четвертого порядка. Однако точное решение уравнений на практике часто и не требуется. Чтобы считать задачу решенной, достаточно бывает отыскать значения корней с требуемой степенью точности. Для получения таких решений разработаны численные методы.
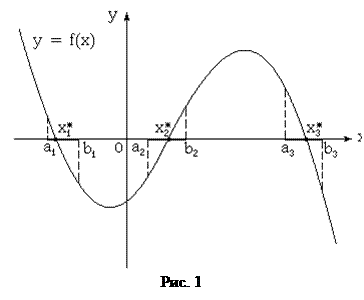Решение нелинейных уравнений осуществляется в два этапа. На первом этапе производится отделение корней, то есть поиск достаточно малых отрезков, каждый из которых содержит единственный корень уравнения. Для этого используется график функции y = f(x), точки пересечения которого с осью абсцисс являются корнями исходного уравнения. Случай, когда корнем уравнения является точка касания графика и оси абсцисс здесь не рассматривается. Это позволяет выделить отрезки [a,b], содержащие только один корень (см. рис 1). При этом для непрерывной функции f(x) будет выполняться неравенство f(a) f(b) < 0.
На втором этапе внутри выделенных отрезков вычисляются значения каждого из корней уравнения с заданной точностью. Для этого используются два основных итерационных подхода: последовательное уточнение первоначального приближения значения корня, взятого из выделенного отрезка, и сужение выделенного отрезка,содержащего корень.
Методы последовательного уточнения начального приближенного значения корня. К этим методам относятся методпростых итераций, метод Ньютона и ряд других. Ониобладают высокойэффективностью, но их применение связано с рядом ограничений, накладываемых на свойства функции f(x).
|
|
Метод простых итераций
Метод основывается на приведении исходного уравнения к форме
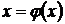
Это преобразованиеможет быть выполнено многими способами.
Например, уравнение
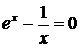
может быть преобразовано как x= e -x или x = ln | 1 / x |.
Далее процесс уточнения корня строится по следующей итерационной схеме
……………
……………
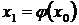
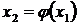
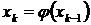
где x 0 - первоначальное приближенное значение корня на отрезке [a, b].
Если последовательностьзначений xk (k = 0, 1, 2,...) имеетконечный предел, то итерационный процесс сходится к точному значению корня x *за бесконечно большое число шагов. Поэтому итерации завершают при выполнении одного из условий:
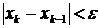или 
,
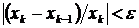где e - требуемая абсолютная или относительная погрешность определения корня, соответственно. Однако, может случиться так, что последовательность значений xk (k = 0, 1, 2,...) не имеет предела. В этом случае метод расходится, и описанная итерационная схема не может быть применена для решения уравнения.
Процесс уточнения корня уравнения методом простых итераций может быть проиллюстрирован графически.
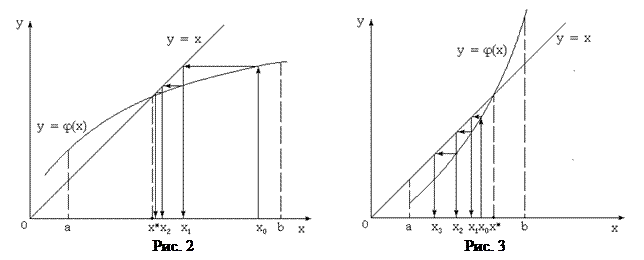
Как видно на рис.2, для выбранной на отрезке [a, b] начальной точки x 0 вычисляется значение функции j (x 0 ). Абсцисса этой точки с помощью графика функции y = x преобразуетсявновое приближение переменной x 1. Далее процесс повторяется, и находятся значения x 2, x 3,..., xk,... до тех пор, пока не будет выполнено условие завершения итерационного процесса по заданной погрешности вычисления корня e. В данном случае итерационный процесс сходится и заданная погрешность вычисления корня достижима. На рис.3 показана ситуация, когда метод итераций расходится. Каждое новое значение xk отстоит все дальше от точного решения уравнения x *и заданная погрешность вычисления недостижима. Такая ситуация характерна для неудачного преобразования уравнения f(x) = 0 к уравнению x = j (x).
|
|
В методе итераций рекомендуется преобразовывать исходное уравнение, основываясь на теореме о его сходимости, которая гласит: есливо всех точках отрезка изоляции [a,b] корня уравнения x = j (x) функция j (x) удовлетворяет условию | j¢(x) | < 1, то итерационный процесс сходится к точному значению корня x *для любого x 0 из отрезкаизоляции.
Исходя из вышесказанного, можно указать еще один способ преобразования исходного уравнениякформе, требуемой методом итераций. Исходное уравнение f(x) = 0 равносильно уравнению x = x + lf(x), где l - отличная от нуля произвольная постоянная. Эта постоянная выбирается из условия сходимости метода | j¢(x) | < 1, считая j (x) = x + l f(x).
Метод Ньютона (I.Newton, 1669)
В данном методе каждое новое приближение к значению корня уравнения f(x) = 0 ищется по следующей итерационной схеме
………………….
………………….
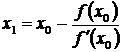
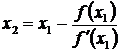
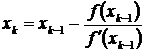
где x 0 - первоначальноеприближенноезначение корня на отрезке [a,b].
Графическая интерпретация работы метода Ньютона представлена на рис.4. Из точки на кривой y = f(x), имеющей абсциссу x 0, проводится касательная до пересечения с осью 0x и абсцисса точки пересечения принимается за новое приближение x 1 значения корня уравнения f(x) = 0. В случае сходимости последовательности вычисляемых значений x 0, x 1,..., xk,... процесс продолжается до тех пор, пока не выполнится условие его завершения по заданной погрешности определения корня e.
|
|
Чтобы последовательность приближений x 0, x 1,..., x k,... сходилась к значению корня x *, необходимо и достаточно выполнение условий следующей теоремы. Еслив окрестности корня x * функция f(x) имеет непрерывные производные f¢(x) и f¢¢(x), для которых справедливо неравенство
,
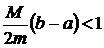тоитерационный процесс сходится к точному значению корнядля любого x 0 из [a, b].
Методы сужения отрезка [a, b], к которымотносятся метод хорд, метод половинного деления и др., не имеют ограничений на функцию f(x), присущих методам последовательного уточнения.
Метод половинного деления (метод бисекций)
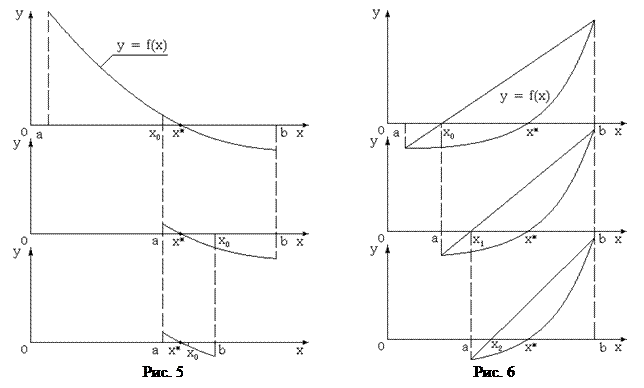
Работа метода иллюстрируется на рис.5. Отрезок изоляции [a, b] корня делится пополам x 0 = (a + b)/2 и в полученной точке вычисляется значение функции. Если f(x 0 ) = 0, то корень найден и расчеты прекращают. В противном случае выбирается новый отрезок, содержащий корень уравнения, из отрезков [a, x 0 ] и [x 0, b]. На концах искомого отрезка функция f(x) должна иметь значения разного знака. Для этого проверяется условие
f(a)f(x 0 ) < 0.
При его выполнении в качестве нового отрезка принимается отрезок [a, x 0 ], в противном случае - [x 0, b]. Процесс сужения отрезка продолжается до тех пор, пока его длина не станет меньше наперед заданного значения абсолютной погрешности e или не будет выполнено условие по относительной погрешности определения корня. При этом за значение корня принимается либо одна из границ суженного отрезка [a, b], либо его середина.
Метод хорд
Идея метода состоит в замене функции f(x) внутри отрезка [a, b] линейной функцией. Точка пересечения x 0графика линейной функции и оси абсцисс принимается за значение одной из границ нового отрезка изоляции корня, который выбирается аналогично методу половинного деления. Далее процесс повторяется и находится x 1 - точка пересечения графика линейной функции нового отрезка с осью абсцисс. Иллюстрацией этого алгоритма является рис.6.
Процесс поиска корня продолжается до тех пор, пока не будет выполнено условие, задающее погрешность его определения.
Для расчета на каждом шаге координаты точки пересечения графика линейной функции и оси абсцисс используются выражения вида:
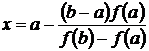
или
.
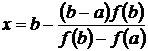