Численные методы решения систем линейных алгебраических уравнений
,
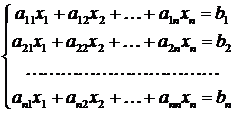записываемых в матричной форме в виде
,
где
,
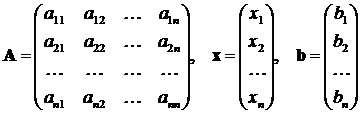делятся на точные и итерационные. Они используются для систем, у которых количество неизвестных равно количеству уравнений и матрица A - не вырождена (ее определитель не равен нулю). Точными методами условно называют методы, которые дают решение задачи посредством конечного числа арифметических операций. Итерационные методы позволяют получить решение системы как предел бесконечной последовательности его приближений. При применении итерационных методов существенным вопросом является вопрос об их сходимости.
Точные методы, к которым относятся метод Гаусса и его разновидности, не имеют дополнительных ограничений на свойства матрицы системы.
Метод Гаусса (K.F.Gau b, 1849)
В основе метода Гаусса лежит идея последовательного исключения неизвестных, приводящая исходную систему с квадратной матрицей к легко разрешимой системе с верхней треугольной матрицей
.
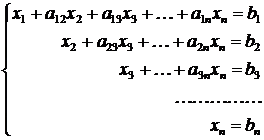Данное преобразование может быть осуществлено многими способами. Однако, все они основаны на свойстве систем, которое заключается в неизменности их решений при умножении любого уравнения на отличную от нуля постоянную или его замене на сумму с любым другим уравнением.
Один из простейших способов исключения состоит в следующем. Первое уравнение системы
,
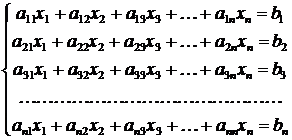которое на этом шаге считается ведущим, нормируется - делится на значение диагонального элемента a 11
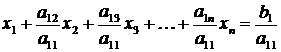
или
,
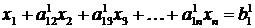где
.
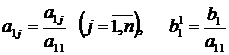Если в исходной системе a 11 = 0, то в качестве первого уравнения следует взять любое другое с ненулевым первым коэффициентом, поменяв их местами. Полученное уравнение умножается на первый коэффициент второго уравнения a 21 и вычитается из него. В результате во втором уравнении пропадает слагаемое a 21 x 1, содержащее первое неизвестное x 1. Такие же операции проводятся со всеми последующими уравнениями. В результате система уравнений принимает вид
|
|
.
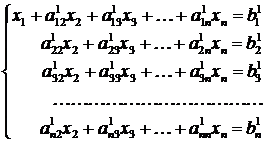Далее процесс повторяется. За ведущее берется второе уравнение и исключается неизвестное x 2 из всех уравнений, начиная с третьего:
.
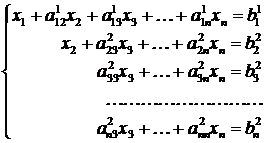Таким образом, за n шагов система уравнений последовательно сводится к треугольному виду, при этом для последнего уравнения выполняется только операция нормирования:
.
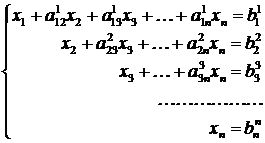Полученная система с верхней треугольной матрицей может быть легко разрешена относительно неизвестных. Последнее уравнение системы определяет значение xn, что позволяет определить xn -1из предпоследнего уравнения как
.
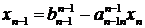Выполняя аналогичные подстановки найденных неизвестных в вышестоящие уравнения, удается определить все компоненты решения xn -2,..., x 2, x 1.
Метод Гаусса дает точное решение, если все исходные данные точны и все вычисления производятся точно. На практике, при выполнении вычислений, неизбежно проводятся округления. Ошибка округлений вносит погрешность в метод Гаусса. Таким образом, при операциях с округленными десятичными числами метод Гаусса дает не точное решение системы линейных алгебраических уравнений, а некоторое приближенное.
Метод Гаусса с выбором главного элемента
Основное накопление погрешностей решения в методе Гаусса происходит на этапе приведения системы к треугольному виду. Механизм накопления этой погрешности заключается в привнесении погрешностей вычисления коэффициентов ведущего уравнения в коэффициенты последующих уравнений при исключении каждого очередного неизвестного. Анализ соотношений метода Гаусса показывает, что погрешности вычисления коэффициентов ведущего уравнения привносятся в соответствующие коэффициенты всех последующих в долях отношений этих коэффициентов к диагональному (главному) коэффициенту ведущего. В связи с этим привносимая погрешность будет тем меньше, чем меньше доли этих отношений. Поэтому в методе Гаусса с выбором главного элемента на каждом шаге исключения i -го неизвестного в качестве ведущего используетсяуравнение (с i -го по n -ое), содержащее максимальный по модулю коэффициент - главныйэлемент. При этом в качестве него может использоваться один из коэффициентов i -го столбца, i -ой строки или всей непреобразованной части матрицы. Первый подход называется выбором главного элементапостолбцу, второй - по строке, а третий - по всейматрице. При использовании двух последних происходит перестановка столбцов матрицы системы. Это приводит к изменению порядка следования компонент вектора неизвестных и требует его восстановления.
|
|
Итерационные методы. К этим методам относятся методпростых итераций, метод Зейделя и ряд других. Методы этой группы обладают высокой эффективностью, но их применение связано с рядом ограничений, накладываемых на свойства матрицы A.
Метод простых итераций
Метод основывается на приведении исходной системы к форме
где D - квадратная матрица, полученная из матрицы A, а p - вектор-столбец, полученный из b. Это преобразованиеможет быть выполнено многими способами. Например, путем разрешения i -го уравнения относительно i -го неизвестного:
|
|
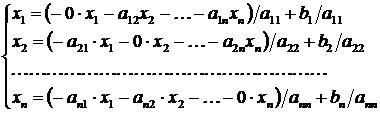
при этом
,
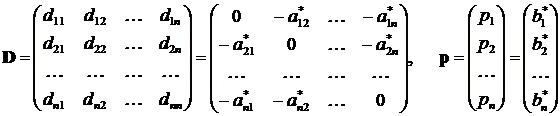где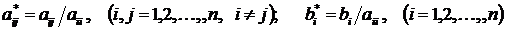 
.
Далее процесс уточнения корня строится по следующей итерационной схеме
……………….
……………….
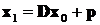
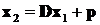
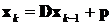
где x 0 - начальное приближение вектора решения системы. То есть
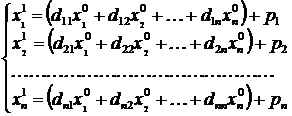
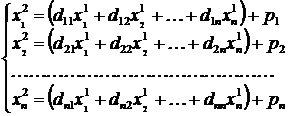
и т.д.
Если последовательность векторов x k (k =0,1,2,...) имеет конечный предел (тоже вектор), то итерационный процесс сходится к точному решению системы x *за бесконечно большое число шагов. Поэтому итерации завершают при выполнении одного из условий:
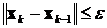или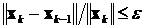 
,
где e - требуемая абсолютная или относительная погрешность определения решения, соответственно, а в качестве нормы вектора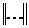 
можно использовать одно из следующих выражений
, 
.
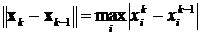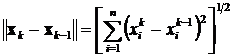Встречаются ситуации, когда из-за плохой сходимости метода приведенные выше условия могут выполниться, хотя решение системы с заданной погрешностью еще не получено. В этом случае в качестве условия завершения итерационного процесса следует использовать условие, основанное на оценке невязок системы
.
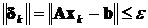Однако, может случиться так, что последовательность векторов x k (k= 0,1,2,...) не имеет предела. Вэтом случаеметод расходится и описанная итерационная схема не может быть применена для решения системы.
Для того, чтобы последовательностьвекторов x k (k =0,1,2,...) при любом начальном векторе x 0 сходилась к решению системы, надо выбрать матрицу D так, чтобы ее норма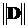 
была меньше единицы. В качестве нормы матрицы можно использовать любое из трех соотношений:
, 
, 
.
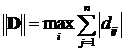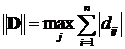Если описанный выше прием формирования итерационной схемы не позволяет получить матрицу D, которая подчиняется условию сходимости, а матрица А - симметрична и положительно определена, то можно поступить следующим образом. Исходная система линейных алгебраических уравнений
приводится к эквивалентному виду
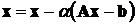
путем переноса произведения Ax в правую часть уравнения, умножения обеих частей уравнения на константу a идобавления к ним вектора x. В результате этого преобразования получается итерационная схема
,
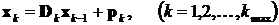где
.
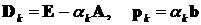Здесь под E понимается единичная матрица.
Параметр ak вычисляется с использованием выражения
,
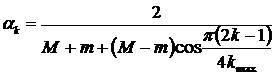где
, 
, 
.
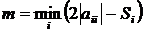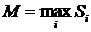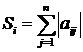Подбирая таким способом ak на каждом шаге процесса итераций, удается получить матрицу D k, подчиняющуюся условию сходимости. Описанный прием называется методом простых итераций с релаксацией.
Если система уравнений
имеет матрицу A, которая не является симметричной и положительно определенной, то надо произвести ее симметризацию. Она заключается в умножении левой и правой частей системы на транспонированную матрицу A T
,
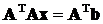что приводит исходную систему к виду
,
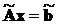где
.
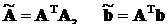Метод Зейделя (L.Seidel, 1874)
Этот метод является разновидностью метода простых итераций. Исходная система приводится к такому же виду, как и в методе простых итераций, но процесс итераций организуется иным образом. Как только на k -й итерациивычислена i -я компонента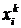 
вектора x k, ее значение используют для вычисления последующих компонент 
, 
,..., 
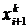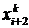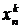этого вектора, не дожидаясь начала следующей итерации. Например
.
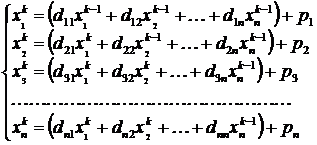Вопрос о сходимости метода Зейделя в общем виде является открытым. Однако известно, что выполнение условия сходимости метода простых итераций гарантирует сходимость метода Зейделя. При этом благодаря особенностям итерационной схемы, метод Зейделя позволяет за то же количество шагов, что и метод простых итераций, получить более точный результат.
Если при решении системы уравнений методом Зейделя итерационный процесс расходится, то могут использоваться описанные выше приемы с релаксацией и симметризацией системы уравнений.