Неравенства и их основные свойства. Доказательство неравенств
Рассмотрим методы доказательства числовых неравенств. Для этого вспомним основные понятия и определения.
Все действительные числа разбиваются на положительные числа, отрицательные числа и число нуль. Далее:
- для того чтобы указать, что число а положительно, пользуются записью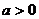 
;
- сумма и произведение положительных чисел также являются положительными числами;
- если число а отрицательно, то число – а положительно (и наоборот)
- для любого положительного числа а найдется положительное рациональное число r, что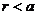 
.
Эти основные факты лежат в основе теории неравенств.
Определение. Неравенство a>b (или, что то же самое, b<a) равносильно тому, что a-b>0.
Определение. Неравенство a<0 означает, что число а отрицательно.
Определение. Неравенство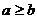 
(или, то же самое, 
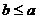) означает, что либо a>b, либо a=b.
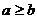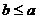Определение. Неравенства a>b и b<a называют строгими неравенствами, а неравенства и называют нестрогими неравенствами.
Наряду с неравенствами вида a>b и 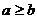определяют двойные неравенства.
Определение. Двойное неравенство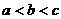 
означает, что a<b и b<c.
Аналогично определяются двойные неравенства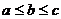 
, 
, 
.
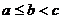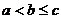Основные свойства неравенств
1. Если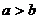 
и 
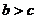, то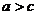 
(транзитивность).
2. Если 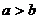, то при любом с имеет место неравенство 
.
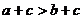3. Если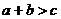 
, то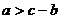 
.
4. Если 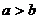и 
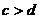, то .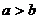
5. Если 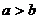, то при 
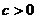верно неравенство 
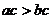, а при 
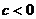верно неравенство 
.
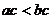6. Если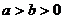 
и 
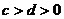, то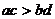 
.
7. Если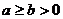 
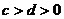и , то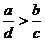 
.
Замечание: при a=b=1, если 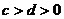, то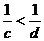 
.
8. Если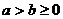 
, то 
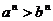, где n – натуральное число.
9. Если 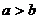, то 
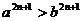, где n – натуральное число.
10. Если 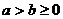, то 
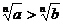, где n – натуральное число.
11. Если 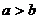, то 
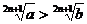, где n – натуральное число.
Следствие. Неравенство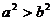 
имеет место тогда и только тогда, когда 
.
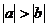Доказательство этих свойств опирается на основные определения. Докажем, например, свойство 5.
Доказательство. Если 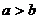, то разность 
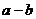, есть число положительное. Следовательно, знак разности 
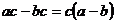совпадает со знаком числа с. При 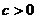эта разность положительна и поэтому 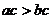, а если 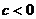, то разность отрицательна и 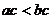, ч.т.д.
Остальные свойства доказываются аналогично.
Основные методы доказательства неравенств
I. Доказательство неравенств с помощью определения
Для доказательства неравенства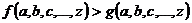 
этим способом на заданном множестве значений переменных a, b, c, …, z составляют разность 
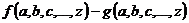и доказывают, что она положительна при всех значениях переменных.
Пример 1. (Неравенство Коши)
Доказать, что при всех 
выполняется неравенство
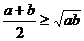- (1)
Доказательство. Составим разность 
и выясним ее знак. Имеем: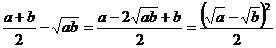 
. Выражение 
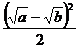неотрицательно при любых значениях (условия определяют существование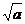 
и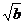 
), причем знак равенства имеет место лишь при a=b. То есть 
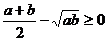, а это означает, что 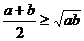, ч.т.д.
Пример 2. Доказать, что если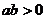 
, то
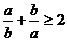(2)
Доказательство. Имеем: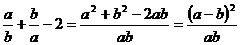 
. Так как 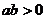, то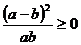 
, причем знак равенства имеет место лишь при a=b. Таким образом, разность 
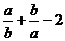неотрицательна и неравенство (2) доказано.
II. Синтетический метод доказательства неравенств
Суть этого метода заключается в том, что с помощью различных преобразований доказываемое неравенство выводят из некоторых опорных (известных) неравенств. В качестве опорных можно использовать следующие неравенства:
а)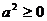 
, б) неравенство Коши (1), в) 
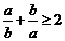, при 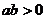, которое является следствием (2), г) 
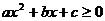при 
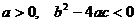, д)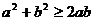 
для всех чисел a и b.
Пример 3. Доказать, что для любых чисел a, b и c имеет место неравенство
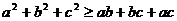(3)
Доказательство. В качестве опорных, выберем неравенства
, 
, 
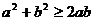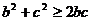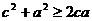
Сложим почленно эти неравенства, а затем разделим обе части полученного неравенства на два. Получим нужное нам неравенство.
Пример 4. Доказать, что для любых неотрицательных чисел a, b, c, d имеет место неравенство
.
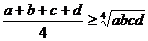Доказательство. Воспользуемся в качестве опорных неравенствами Кош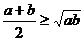и 
и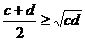 
. Тогда получим:
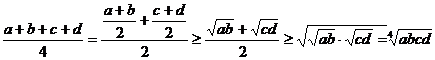, ч.т.д.