Метод доказательства «от противного» высказывания «из А следует В» применяют в следующей форме: считают истинным высказывание «не выполняется В» и пытаются вывести отсюда справедливость высказывания «не выполняется А». Если это удается, то получается противоречие, из которого следует, что предположение о неверности А – ошибочно. Покажем, как этот метод применяется при доказательстве неравенств.
Пример 5. Доказать, что для любого числа а выполняется неравенство
.
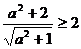Доказательство. Предположим противное, что для некоторого числа а рассматриваемое неравенство неверно, то есть имеет место неравенство:
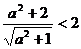. По свойству 5 можно умножить обе части неравенства на положительное число 
, при этом знак неравенства не изменится: 
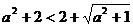. По свойству 2 можно вычесть из обеих частей неравенства выражение 
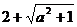. После преобразований правой части получим:
, то есть 
. Последнее неравенство не выполняется ни при каком значении а, так как правая часть неравенства не может принимать отрицательные значения. Полученное противоречие доказывает верность исходного неравенства.
IV. Доказательство неравенств методом математической индукции
Доказательство неравенств методом математической индукции проводится по следующей схеме:
1. Проверяется неравенство для некоторого начального значения n, например, для n=1.
2. Предполагается, что неравенство выполняется для n=k.
3. Доказывается, что тогда неравенство выполняется для n=k+1.
Пример 6. Доказать, что если n = 2, 3, 4,…, то 
.
Доказательство. 1. При n = 2 неравенство верно: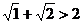 
. Это можно проверить, возведя обе части неравенства в квадрат (т.к. обе части неравенства положительны, это можно сделать по свойству 8). 2. Предположим, что неравенство выполняется для n=k, то есть 
. 3. Докажем, что тогда неравенство выполняется для n=k+1, то есть 
. Так как , то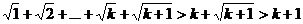 
, так как 
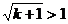для вех значений k>1.
Согласно принципу математической индукции, можно сделать вывод о том, что неравенство выполняется при всех значениях n = 2, 3, 4,….
Аналогично методом математической индукции можно доказать неравенство Коши в общем случае. Мы не будем приводить доказательство по причине его сложности.
Неравенство для среднего арифметического и среднего геометрического n неотрицательных чисел (неравенство Коши)
Если 
- любые неотрицательные числа, то
(4)
Равенство имеет место лишь при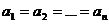 
В заключение приведем формулировку еще одного важного неравенства.
Неравенство Коши – Буняковского
Для любых действительных чисел 
выполняется неравенство:
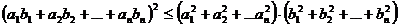(5)
Равенство в (4) имеет место тогда и только тогда, когда числа 
и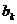 
пропорциональны, то есть существуют такие числа 
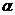и 
, что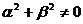 
и для всех k=1,2,…,n выполняется равенство
.
КОНТРОЛЬНЫЕ ЗАДАНИЯ
Предлагаемые ниже задачи являются контрольным заданием по математике для учащихся 10 классов. Для зачета вам рекомендуется решить не менее 6 задач. Правила оформления, адрес и другая полезная информация – в конце журнала. Желаем Вам успехов.
М.10.1.1. Докажите, что для любых действительных чисел a и b выполняется неравенство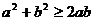 
.
Указание: Перенести все члены в левую часть, преобразовать и определить знак полученного выражения.
М.10.1.2. Доказать, что для любых действительных чисел a и b выполняется неравенство
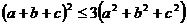
Указание: Перенести все члены в левую часть, преобразовать и определить знак полученного выражения.
М.10.1.3. Докажите, что есл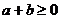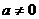и 
, 
и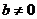 
, то выполняется неравенство
Указание: Перенести все члены в левую часть, преобразовать и определить знак полученного выражения.
М.10.1.4. Доказать, что если 
, то верно неравенство
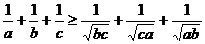
Указание: Обозначить 
и использовать в качестве опорного неравенство (3).
М.10.1.5. Доказать, что для любых положительных чисел a, b и c выполняется неравенство
Указание: Воспользоваться три раза неравенством (1), где в качестве слагаемых взять, соответственно,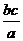 
, 
в первом неравенстве, , 
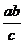во втором неравенстве и 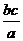, 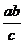в третьем неравенстве.
М.10.1.6. Доказать, что для любых положительных чисел a, b и c выполняется неравенство
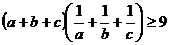
Указание: Воспользоваться в качестве опорного неравенством Коши - Буняковского.
М.10.1.7. Доказать, что если , то верно неравенство
Указание: доказательство провести методом от противного. Возвести обе части в квадрат и получить противоречие с неравенством Коши.
М.10.1.8. Доказать, что при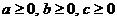 
верно неравенство
.
Указание: доказательство провести методом от противного. Возвести обе части в квадрат и после преобразований сравнить знак левой и правой частей неравенства.
М.10.1.9. Доказать, что при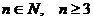 
верно неравенство
Указание: доказательство провести методом математической индукции.
М.10.1.10. Доказать, что при 
верно неравенство
Указание: доказательство провести методом математической индукции.