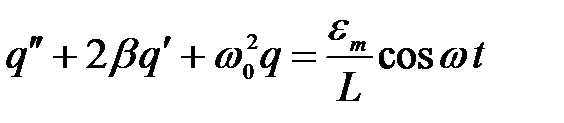. (1)
Уравнение (1) является неоднородным линейным дифференциальным уравнением второго порядка. Такого типа уравнения описывают поведение широкого класса колебательных систем (электрических, механических) под влиянием внешнего периодического воздействия (внешней ЭДС или внешней силы).
Общее решение уравнения (1) складывается из общего решения q 1 однородного дифференциального уравнения 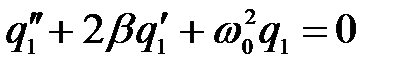(2)
(2)
и любого частного решения q 2 неоднородного уравнения (1)
.
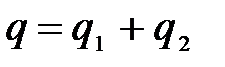Вид общего решения однородного уравнения (2) зависит от величины коэффициента затухания b. Нас будет интересовать случай слабого затухания b << w0. При этом общее решение уравнения (2) имеет вид
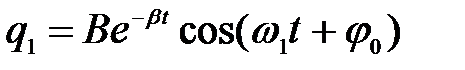, (3)
где B и j 0 – постоянные, задаваемые начальными условиями.
Решение (3) описывает затухающие колебания в контуре. Входящие в (3) величины:
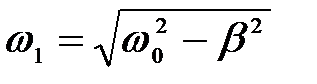– циклическая частота затухающих колебаний;
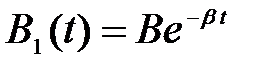– амплитуда затухающих колебаний;
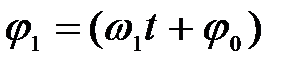– фаза затухающих колебаний.
Частное решение уравнения (1) ищем в виде гармонического колебания, происходящего с частотой, равной частоте w внешнего периодического воздействия – ЭДС, и отстающего по фазе на y от него
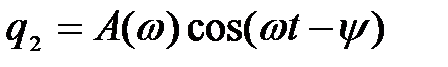, (4)
где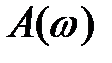 
– амплитуда вынужденных колебаний, зависящая от частоты.
Подставим (4) в (1) и получим тождество
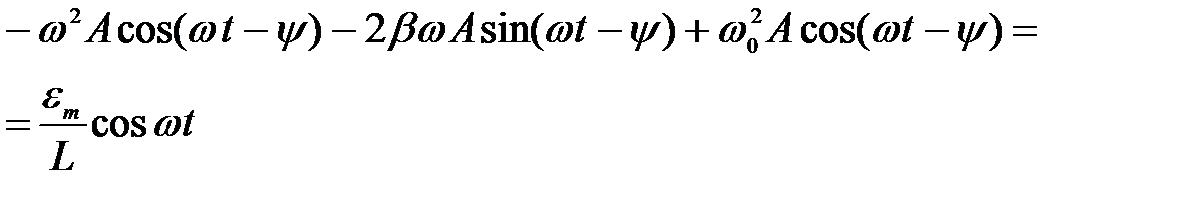
Чтобы сравнить фазы колебаний, используем тригонометрические формулы приведения
,
.
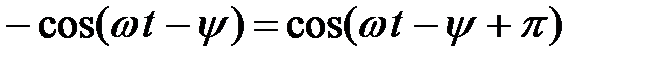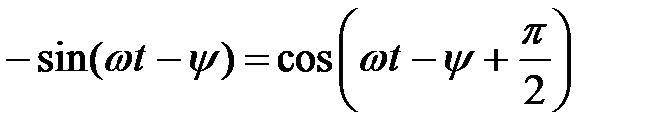Тогда наше уравнение перепишется в виде
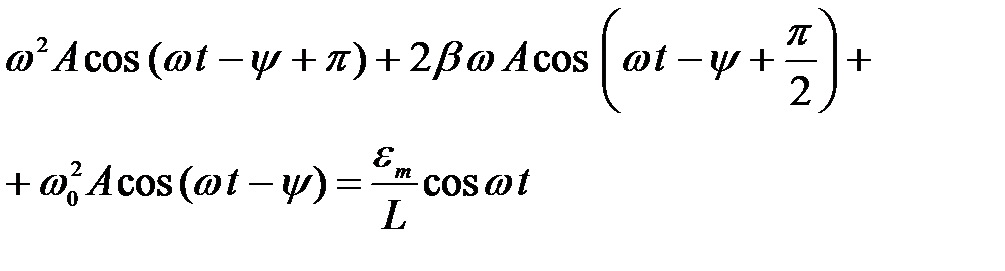
Представим колебания в левой части полученного тождества в виде векторной диаграммы (рис. 2).
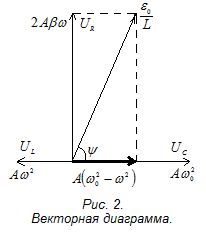Третье слагаемое, соответствующее колебаниям на емкости С, имеющее фазу (wt – y) и амплитуду 
, изобразим горизонтальным вектором, направленным вправо.
Первое слагаемое левой части, соответствующие колебаниям на индуктивности L, изобразится на векторной диаграмме вектором, направленным горизонтально влево (его амплитуда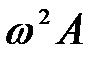 
).
Второе слагаемое, соответствующие колебаниям на сопротивлении R, изобразим вектором, направленным вертикально вверх (его амплитуда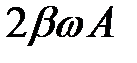 
), т. к. его фаза на p/2 отстает от фазы первого слагаемого.
Так как сумма трех колебаний слева от знака равно дает гармоническое колебание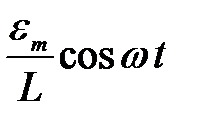 
, то векторная сумма на диаграмме (диагональ прямоугольника) изображает колебание с амплитудой 
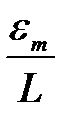и фазой wt, которая на y опережает фазу колебаний третьего слагаемого.
Из прямоугольного треугольника по теореме Пифагора можно найти амплитуду A (w)
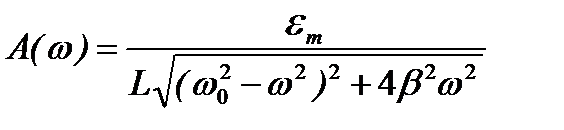(5)
и tgy как отношение противолежащего катета к прилежащему катету.
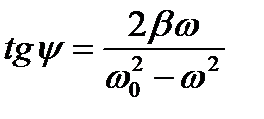. (6)
Следовательно, решение (4) с учетом (5) и (6) примет вид
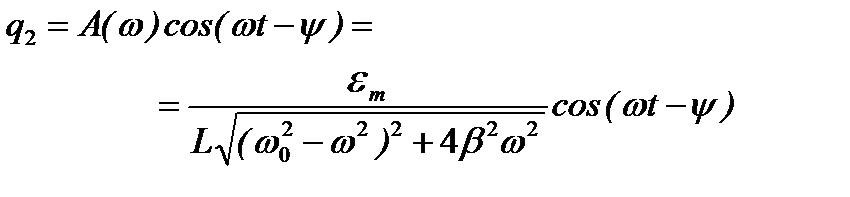. (7)
Общее решение дифференциального уравнения (1) является суммой q 1 и q 2
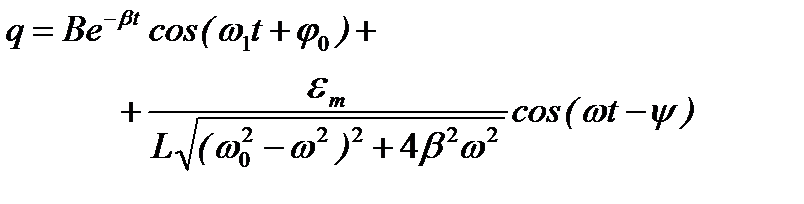. (8)
Формула (8) показывает, что при воздействии на контур периодической внешней ЭДС в нем возникают колебания двух частот, т.е. незатухающие колебания с частотой внешней ЭДС w и затухающие колебания с частотой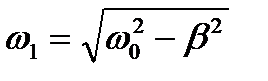 
. Амплитуда затухающих колебаний 
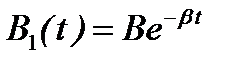со временем становится пренебрежимо малой, и в контуре остаются только вынужденные колебания, амплитуда которых не зависит от времени. Следовательно, установившиеся вынужденные колебания описываются функцией (4). То есть в контуре возникают вынужденные гармонические колебания, с частотой, равной частоте внешнего воздействия, и амплитудой 
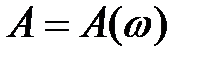, зависящей от этой частоты (рис. 3 а) по закону (5). При этом по фазе вынужденное колебание отстает на y от вынуждающего воздействия.
Продифференцировав выражение (4) по времени, найдем силу тока в контуре
,
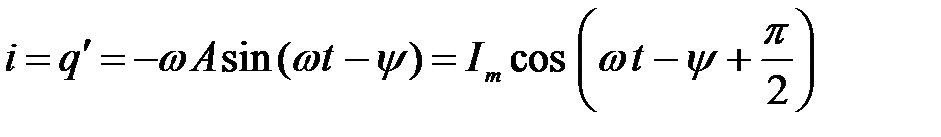где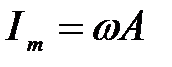 
– амплитуда силы тока.
Запишем это выражение для силы тока в виде
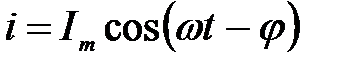, (9)
где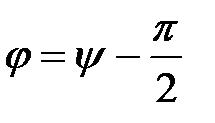 
– сдвиг по фазе между током и внешней ЭДС.
В соответствии с (6) и рис. 2
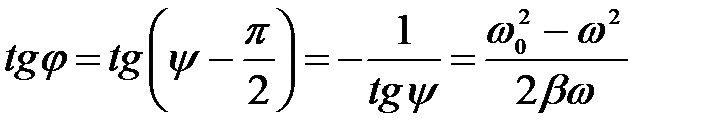. (10)
Из этой формулы следует, что сдвиг по фазе между током и внешней ЭДС зависит, при постоянном сопротивлении R, от соотношения между частотой, вынуждающей ЭДС w и собственной частотой контура w 0.
- Резонанс в RLC-контуре. Резонансная частота. Рассмотреть резонанс тока, заряда (напряжения) на контуре.
Если w = w 0 (резонансная частота), то j = 0, т. е. сила тока и ЭДС колеблются в одинаковой фазе.
| w р1 w р2 w |
| A |
| Рис. 3 а. Амплитуды колебаний заряда. |
| R 2 |
| R 1 |
| R 1 > R 2 |
| w р1 < w р2 |
| w o w |
| Im |
| Рис. 3 б. Амплитуды колебаний силы тока. |
| R 3 |
| R 2 |
| R 1 |
| R 1 > R 2 > R 3 |
Резонанс – это явление резкого возрастания амплитуды колебаний при совпадении частоты внешней, вынуждающей силы с собственной частотой колебательной системы.
Амплитуду силы тока можно преобразовать к виду
. (11)
Из (11) следует, что амплитуда силы тока в контуре зависит от частоты внешней ЭДС w. График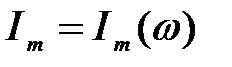 
представлен на рис. 3 б.
С возрастанием w амплитуда силы тока возрастает, затем достигает максимума и при дальнейшем увеличении w асимптотически спадает до нуля.
Очевидно, что максимальное значение сила тока достигает при
,
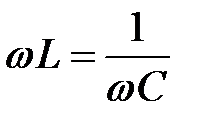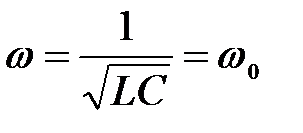
Максимальное значение силы тока при w = w 0 равно
.
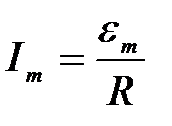Напряжение на активном сопротивлении R найдем из закона Ома
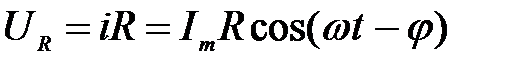. (12)
Разделив выражение для заряда (4) на емкость конденсатора С, получим напряжение на конденсаторе
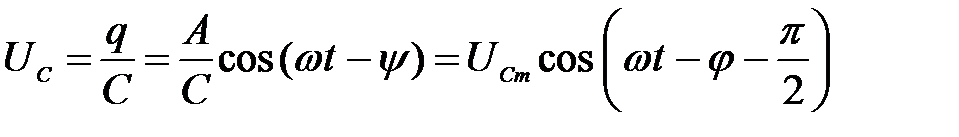, (13)
где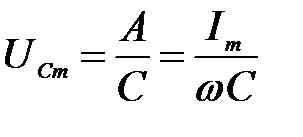 
– амплитуда напряжения на конденсаторе.
Напряжение на катушке индуктивности
,
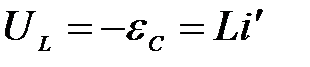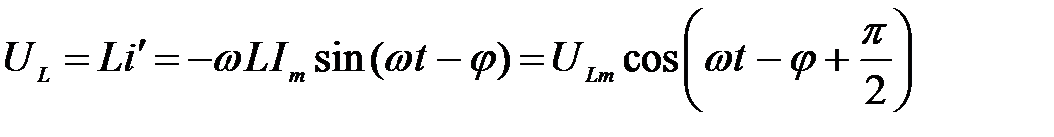, (14)
где 
– амплитуда напряжения на катушке индуктивности.
Таким образом, напряжения на катушке индуктивности (14) и на конденсаторе (13) зависят от частоты внешней ЭДС.
Если w = w 0, то
а) из (10) следует, что j = 0, т.е. сдвиг фазы между током I и внешней ЭДС при резонансе равен нулю;
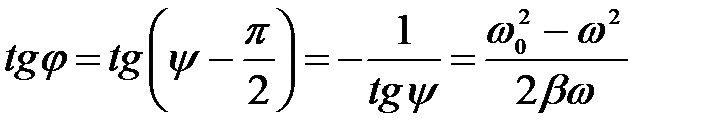. (10)
Из этой формулы следует, что сдвиг по фазе между током и внешней ЭДС зависит, при постоянном сопротивлении R, от соотношения между частотой, вынуждающей ЭДС w и собственной частотой контура w 0.
б) из (12) следует, что сдвиг фазы между током I и напряжением на активном сопротивление UR равен нулю;
в) из (13) следует, что напряжение на конденсаторе UС отстает по фазе от тока I на p /2;
г) из (14) следует, что напряжение на катушке индуктивности UL опережает по фазе ток I на p /2;
При w = w 0 возникает резонанс напряжений. При этом
UL = – UC, т.е. напряжение на емкости и индуктивности равны по величине и противоположны по фазе. Напряжение на реактивных сопротивлениях точно компенсируют друг друга и, следовательно, напряжение на активном сопротивлении равно ЭДС: UR = e.
При резонансе w = w 0 и период колебаний
.
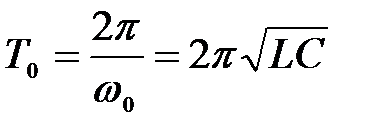22. Волны. Продольные и поперечные волны. Вывод уравнения плоской волны. Длина волны и волновое число.
Волна это процесс распространения колебаний в пространстве.
Волны бывают продольные и поперечные.
Продольная волна – это волна, где колебания происходят вдоль направления распространения волны.
Поперечная волна – это волна, где колебания происходят перпендикулярно направлению распространения волны.