Задача 9
УСТОЙЧИВОСТЬ ЦЕНТРАЛЬНО-СЖАТОГО СТЕРЖНЯ
Условие задачи
Стержень, схема которого приведена в табл. 9.1, сжат силой, приложенной в центре тяжести сечения. Длина l стержня, вид материала и параметры стержня σ а, σ b, λ0, λпред из этого материала заданы в табл. 9.2. Варианты формы и размеров поперечного сечения указаны в табл. 9.3, 9.4.
Требуется:
1. Определить допускаемую силу 
.
2. Найти критическое значение сжимающей критической силы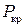 
и запас устойчивости по допускаемой силе 
Теоретические основы решения
В практике часто встречаются случаи нагружения элементов продольной силой, при которых возможна потеря устойчивости. Такие элементы рассматривается как стержень под действием сжимающей продольной силы Р или, как принято говорить, рассматривается центрально-сжатый стержень. Такая расчётная схема применяется при расчёте стоек оборудования, стержней механизмов, несущих колонн, стержней ферм др.
При определённом значении силы происходит внезапное искривление стержня и изменение первоначальной прямолинейной формы упругого равновесия, – это потеря устойчивости стержня (рис. 9.1, а). Значение силы называют критической Р кр, тогда критическое напряжение в стержне равно
,
где А ‒ площадь поперечного сечения стержня. Опасность потери устойчивости не только во внезапности, но и в том, что она происходит при критическом напряжении 
, которое может оказаться существенно меньше допускаемого: 
.
Способность стержня сохранять начальную форму упругого равновесия под нагрузкой называется устойчивостью. Стержень устойчив, если сила и напряжение не превышают определённых допускаемых значений, поэтому условие устойчивости имеет вид:
,…………………(9.1)
где n у ─ коэффициент запаса устойчивост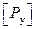и, 
и 
─ допускаемые на устойчивость сила и напряжение. Коэффициент запаса устойчивости зависит от назначения стержня и его материала. Так для стальных стержней, используемых в технике, 
, для дерева 
, для чугуна .
Необходимо заметить,что теряют устойчивость не только центрально-сжатые стержни, но и многие другие конструкции, расчётная схема которых совершенно другая, например, пластины и оболочки. Устойчивость – это большой раздел механики деформируемых тел.
Р кр
| 
|
| а | Б |
Рис. 9.1
Величина критической силы 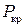для центрально сжатого стержня зависит от его важной геометрической характеристики ‒ гибкости стержня λ, значение которой определяют как
, (9.2)
где 
– коэффициент приведения длины стержня, он указан на расчётной схеме стержня; 
– минимальный радиус инерции сечения, здесь 
– минимальный момент инерции сечения, этим учитываем, что потеря устойчивости происходит в плоскости наименьшей жёсткости, А -площадь сечения.
На рис. 9.1, б дана диаграмма критических напряжений 
, на которой прослеживается три зависимости этих напряжений от гибкости стержня. По величине гибкости стержней имеем три группы стержней: III-я группа ‒ длинные стержни; II-я ‒ средние и I-я ‒ короткие. Ввиду этого формула для вычисления силы 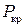выбирается в зависимости от величины гибкости λ, найденной по (9.2) для конкретного центрально-сжатого стержня.
При гибкости стержня λ, удовлетворяющей условию
λ ≥ 
,
имеем длинные стержни (III-я группа). Здесь ‒ предельная гибкость стержня, которая зависит от свойств материала стержня. Её значение определяется как
,
где Е ‒ модуль упругости материала, σпц ‒ егопредел пропорциональности.
Для длинных стержней используется формула Эйлера
. (9.3)
При гибкости стержня λ, удовлетворяющей условию
λ0 ≤ λ ≤ λпред,
имеем средние стержни (II-я группа). Критическую силу 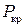для них вычисляют по эмпирической формуле Ясинского-Тетмайера
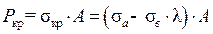. (9.4)
Значения величин Ϭ а, Ϭ в, 
и нужно взять из табл.9.2, они получены в зависимости от вида материала и гибкости стержня.
Если гибкость стержня λ≤ λ0,имеем короткие стержни (I-я группа), они не теряют устойчивости и рассчитываются на прочность.
Для расчётов сжатых стержней создано условие устойчивости, которое справедливо для всех трёх групп стержней. Считая, что в сечении площадью А напряжения равны 
, условие устойчивости записывают в виде
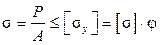, (9.5)
где 
- коэффициент уменьшения основного допускаемого напряжения 
. Коэффициент ещё называют коэффициентом продольного изгиба. Он изменяется в пределах 0 ÷ 1. Значения для некоторых материалов приведены в табл. 9.5. Условие (9.5) называют условием устойчивости по коэффициенту уменьшения основного допускаемого напряжения , или условием устойчивости по коэффициенту .
Пример решения задачи 9
Для центрально-сжатого стержня (рис. 9.2) длина стержня l = 4 м. Материал стержня ‒ сталь Ст. 5, вид поперечного сечения стержня задан схемой (рис. 9.2, б). Значение отрезка а равно а = 30 мм = 3 см.
1. Определение допускаемой силы.
Условие устойчивости по коэффициенту φ (9.5) содержит допускаемое напряжение на устойчивость 
.
Тогда значение допускаемой силы [ P у] для центрально-сжатого стержня равно
. (9.6)
Для вычисления [ P у] нужно знать площадь А поперечного сечения заданного стержня и значение коэффициента 
, которое выбирается из табл.9.6 по значению гибкости данного стержня 
, вычисляемой по формуле (9.2). Подставляем в эту формулу m=0,5 (он указан на схеме стержня); – минимальный момент инерции заданного сечения ‒ это один из двух главных моментов инерции сечения I max и I min. Главныемоменты инерции ̶ это моменты инерции относительно так называемых главных осей, в которых центробежный момент инерции равен нулю. Для выполнения расчётов найдём значения I max, I min и возьмём I min.
| 
|
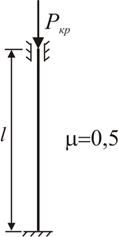
| А | Б |
Рис. 9.2
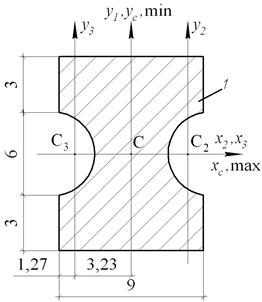
Сначала, используя заданное значение a = 3 см, вычертим сечение в масштабе и проставим числовые значения характерных размеров (рис. 9.3, б).
Рассматриваемое сечение имеет следующие особенности.
Во первых, сечение имеет две оси симметрии, поэтому центр тяжести всего сечения находится на их пересечении − в точке С 1. Через эту точку проведём центральные оси всего сечения xс и yс (рис. 9.3, б).
Во вторых, для рассматриваемого симметричного сечения центробежный момент инерции в осях xс и yс равен нулю, и это означает, что центральные оси всего сечения xс и yс есть главные оси, и центральные моменты инерции сечения 
и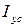 
есть искомые главные моменты инерции I max, I min.
В третьих, рассматриваемое сечение ‒ составное, и моменты инерции нужно вычислять, используя моменты инерции отдельных фигур, составляющих сечение. Сечение можно представить состоящим из следующих простых фигур: прямоугольника высотой 4 а =12мм и шириной 3 а = 9ммидвух вырезов в виде полукругов диаметром 2 а= 6мм,т. е. составное сечение разложим на отдельные элементы (или фигуры). Присвоим им индексы i = 1, 2,3.
| 
|
| а ─ Заданная схема сечения | б ─ Чертёж сечения |
|
|
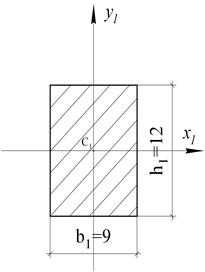
| в ─ 1-й элемент | г ─ 2-й и 3-й элементы |
Рис. 9.3
Изобразим эти элементы отдельно, нанесём их центры тяжести и через точки проведём собственные оси каждого элемента (см. рис. 9.3, в, г). Заметим, что центр тяжести полукруга удалён от диаметра (см. табл. П.6 Приложения к данному пособию) на расстояние, равное
мм.
Оси элементов перенесём на составное сечение (рис. 9.3, б).
Возьмём за вспомогательные оси координат оси (x 1, y 1). Тогда координаты центра тяжести всего сечения равны нулю: xс =0, yс =0, и координаты центра тяжести каждой фигуры следующие:
, 
, 
.
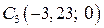Вычислим центральные моменты инерции всего сечения, используя формулы моментов инерции относительно параллельных осей:
, (9.7)
в которые входят геометрические характеристики i -элементов cечения: площадь Аi, осевые Ixi, Iyi моменты инерции относительно собственных осей элементов (xi, yi); и расстояния между осями ai = yi - y c, bi = xi - x c.
Значения площади и моментов инерции элементов cечения относительно собственных осей элементов подсчитаем по формулам, представленным в табл. П.6 Приложения. Необходимо сделать следующее примечание: для отверстий площадь и моменты инерции считаем отрицательными. В нашем примере отверстиями являются полукруги, для них площадь и моменты инерции принимаем со знаком «- ».
Для 1 -го элемента (прямоугольника) получим
см2, 
см4,
см4.
Для 2 -го и 3 -го элементов (полукруга) получим:
см2,
см4,
см4.
Теперь по (9.7) вычислим осевые моменты инерции всего сечения. Осевой момент инерции относительно оси x c равен
см4,
Осевой момент инерции относительно оси y c
см4.
Найденные центральные моменты инерции есть главные моменты инерции сечения. Укажем значения главных моментов инерции I max, I min:
см4, 
см4.
Потеря устойчивости происходит в плоскости минимального момента инерции I min = 563 мм4, поэтому при вычислении гибкости стержня радиус инерции равен
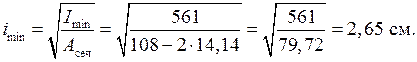
Теперь подсчитаем гибкость стержня по (9.2),
Из табл. 9.5 выписываем соотношения для 2-х ближайших значений 
(λ = 70 и λ = 80) и с помощью прямой пропорции (или интерполирования) находим нужное значение .
Имеем: при гибкости λ = 70 ̶ коэффициент φ = 0,81,
при гибкости λ = 80 ̶ коэффициент φ = 0,75.
Нужное значение коэффициента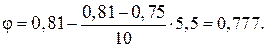 
Теперь найдём значение допускаемой силы по (9.6):
= 