Т.И. Анисимова
Сборник задач по высшей математике
(линейная алгебра и аналитическая геометрия)
Елабуга - 2005
Печатается по решению Ученого совета Елабужского государственного педагогического университета от 2005 (протокол №)
Кафедра математического анализа
Рецензенты:
Кандидат физико-математических наук,
доцент Хафизов Ш.Г.
Кандидат физико-математических наук,
Доцент Миронов Н.П.
Анисимова Т.И. Сборник задач по высшей математике(линейная алгебра и аналитическая геометрия). Учебное пособие для студентов технолого-экономического факультета.
© Елабужский государственный педагогический университет, 2005
Определители

Символ вида
Δ =  ,
,
где  некоторые действительные числа, называется определителем второго порядка.
некоторые действительные числа, называется определителем второго порядка.
Символ вида
Δ =  ,
,
где  некоторые действительные числа, называется определителем третьего порядка.
некоторые действительные числа, называется определителем третьего порядка.
Определитель второго порядка вычисляется по следующей схеме 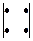 =
= 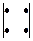 -
- 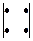 ,
,
т.е.
Δ =  =
=  .
.
При вычислении определителей третьего порядка удобно пользоваться правилом Саррюса:
Δ = 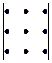 =
= 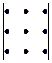 -
- 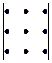 , т.е.
, т.е.
Δ =  = (
= (
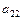
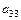 +
+ 
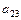
 +
+ 
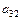
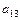 ) – - (
) – - (
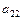
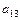 +
+ 

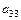 +
+ 
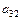
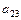 ).
).
Пример 1. Вычислить определитель  .
.
Решение.  = 2·6 - 5·(-3) = 12 – (-15) = 12 + 15 = 27.
= 2·6 - 5·(-3) = 12 – (-15) = 12 + 15 = 27.
Пример 2. Вычислить определитель  .
.
Решение.
 = (5·1· (-3) +6· (-2) · (-4) + 3·0·1) - (6·1·1+5·0· (-4) + 3· (-2) · (-3))= = (-15 + 48 +0) – (6 + 0 + 18) = 33 – 24 = 9.
= (5·1· (-3) +6· (-2) · (-4) + 3·0·1) - (6·1·1+5·0· (-4) + 3· (-2) · (-3))= = (-15 + 48 +0) – (6 + 0 + 18) = 33 – 24 = 9.
Минором некоторого элемента  , определителя п –го порядка называется определитель (п – 1) порядка, полученный из исходного путем вычеркивания строки и столбца, на пересечении которых находится выбранный элемент. Обозначается минор
, определителя п –го порядка называется определитель (п – 1) порядка, полученный из исходного путем вычеркивания строки и столбца, на пересечении которых находится выбранный элемент. Обозначается минор  .
.
Например, для определителя Δ = 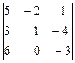
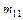 =
= 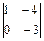 ,
,
 =
=  .
.
Алгебраическим дополнением элемента  определителя называется его минор, взятый со знаком «+», если сумма i + j
определителя называется его минор, взятый со знаком «+», если сумма i + j  четное число, и со знаком «-», если эта сумма нечетная. Обозначается
четное число, и со знаком «-», если эта сумма нечетная. Обозначается 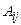 , где
, где 
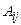 =
= 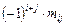 .
.
Например, для определителя Δ = 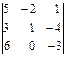
 =
=  = =
= =  = (1·3) – (0· (-4)) = 3,
= (1·3) – (0· (-4)) = 3, 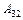 =
= 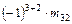 = = -1·
= = -1·  = - (5· (-4) – -3·1) = -(-20 – 3) = 23.
= - (5· (-4) – -3·1) = -(-20 – 3) = 23.
Свойства определителей:
1. Определитель не изменится, если его строки заменить столбцами и наоборот;
2. При перестановке двух параллельных строк или столбцов определитель меняет знак;
3. Определитель, имеющий две одинаковые строки или два одинаковых столбца, равен нулю;
4. Общий множитель элементов какой-либо строки или столбца определителя можно вынести за знак определителя;
5. Определитель не изменится, если к элементам одной строки или одного столбца прибавить соответствующие элементы параллельной строки или столбца, умноженные на любое число;
6. Определитель равен сумме произведений элементов некоторой строки или столбца на соответствующие им алгебраические дополнения.
Пример 3. Вычислить определитель 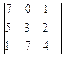 , разложив его по элементам первой строки.
, разложив его по элементам первой строки.
Решение.  = 7·
= 7·  + 0·
+ 0· 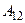 + 1·
+ 1· 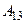 = 7·
= 7· 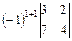 + 0 + +
+ 0 + +  = 7·(3·4 - 7·2) + (5·7 - 1·3) = 7·(-2) +32 = -14 + 32 = 18.
= 7·(3·4 - 7·2) + (5·7 - 1·3) = 7·(-2) +32 = -14 + 32 = 18.
Упражнения:
1. Вычислить определители второго порядка
а)  ; б)
; б)  ; в)
; в)  .
.
2. Вычислить определители третьего порядка
а)  ; б)
; б)  ; в)
; в)  .
.
3. Вычислить определитель третьего порядка, разложив его по элементам какой-либо строки или какого-либо столбца
а) 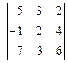 ; б)
; б) 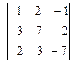 ; в)
; в)  .
.
Матрицы
Матрицей называется прямоугольная таблица чисел, содержащая т строк и п столбцов. Матрица записывается в виде
А = 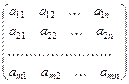 ,
,
или кратко А =  , где i – номер строки, j – номер столбца.
, где i – номер строки, j – номер столбца.
Матрицу А называют матрицей размера т × п и пишут  . Элементы матрицы, стоящие на диагонали, идущей из верхнего левого угла, образуют главную диагональ.
. Элементы матрицы, стоящие на диагонали, идущей из верхнего левого угла, образуют главную диагональ.
Матрица, у которой число строк равно числу столбцов, называется квадратной. Квадратная матрица, у которой все элементы, кроме элементов главной диагонали, равны нулю, называется диагональной. Диагональная матрица, у которой каждый элемент главной диагонали равен единице, называется единичной.
Матрица 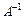 называется обратной к матрице А, если
называется обратной к матрице А, если 
 , Е – единичная матрица. Причем
, Е – единичная матрица. Причем
 ,
,
где Δ – определитель матрицы А, 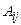 - алгебраические дополнения.
- алгебраические дополнения.
Действия над матрицами
1. Сложение. Операция сложения матриц вводится только для матриц одинаковых размеров. Суммой двух матриц 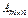 =
=  и
и  называется матрица
называется матрица 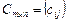 , такая, что
, такая, что 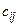 =
=  +
+ 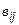 .
.
Пример1. Найти сумму матриц
 и
и 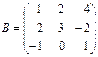 .
.
Решение. 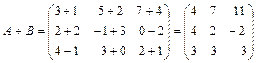 .
.
2. Умножение на число. Произведением матрицы  =
=  на число k называется матрица
на число k называется матрица 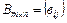 такая, что
такая, что  .
.
Пример 2. Найти 2 А + 3 В, если
 ,
, 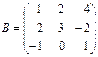 .
.
Решение. 2 А = 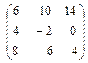 , 3 В =
, 3 В =  ,
,
2 А + 3 В =  .
.
3. Произведение матриц. Операция умножения двух матриц вводится только для случая, когда число столбцов первой матрицы равно числу строк второй матрицы. Например, произведением матрицы  на матрицу
на матрицу  является матрица
является матрица 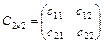 такая, что
такая, что  =
= 
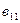 +
+ 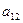
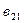 +
+ 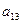
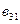 (элемент матрицы-произведения, стоящий в i -ой строке и j -ом столбце, равен сумме произведений соответственных элементов i -ой строки матрицы А и j -го столбца матрицы В);
(элемент матрицы-произведения, стоящий в i -ой строке и j -ом столбце, равен сумме произведений соответственных элементов i -ой строки матрицы А и j -го столбца матрицы В);  =
= 
 + +
+ + 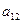
 +
+ 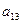
 ;
;  =
= 
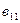 +
+
+ 
 +
+ 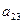
 ;
;  =
= 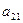
 + +
+ + 
 +
+ 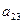
 .
.
Следует помнить, что АВ ≠ ВА.
Пример 3. Найти произведение матриц  и
и  .
.
Решение. 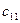 = 1·1+2·3 +3·2 = 13;
= 1·1+2·3 +3·2 = 13;  = 1·2 + 1·0 +3·0 = 2;
= 1·2 + 1·0 +3·0 = 2;  = 0·1 + +4·3 +1·2 = 14;
= 0·1 + +4·3 +1·2 = 14; 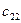 = 0·2 + 4·0 +1·0 =0. Получаем
= 0·2 + 4·0 +1·0 =0. Получаем 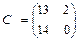 .
.
Упражнения:
1. Вычислить а) 3 А + 2 В, если
 ,
,  ;
;
б) 2 А – В, если
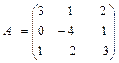 ,
,  ,
,
в)  , если
, если 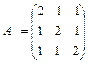 , Е – единичная матрица.
, Е – единичная матрица.
2. Умножить матрицы
а)  ,
,  ;
;
б) 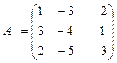 ,
, 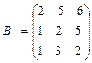 , в)
, в)  ,
,  .
.
3. Найти обратную матрицу для матриц:
а)  , б)
, б) 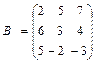 , в)
, в)  .
.
Системы линейных уравнений
Система трех линейных уравнений с тремя неизвестными х1, х2, х3 имеет вид:

где 
 - коэффициенты системы,
- коэффициенты системы,  - свободные члены.
- свободные члены.
Определитель третьего порядка Δ, составленный из коэффициентов при неизвестных, называется определителем системы. Если Δ ≠ 0, то единственное решение системы выражается формулами Крамера:

где 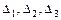 - определители третьего порядка, получаемые из определителя Δ заменой первого, второго или третьего столбца соответственно свободными членами
- определители третьего порядка, получаемые из определителя Δ заменой первого, второго или третьего столбца соответственно свободными членами  .
.
Матрица
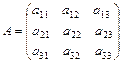
называется матрицей системы.
Расширенной матрицей системы называется матрица вида


 .
.
К элементарным преобразованиям матрицы относятся:
1) перемена местами каких-либо двух строк матрицы;
2) умножение матрицы или какой-либо отдельной ее строки на некоторое ненулевое число;
3) прибавление к элементам какой-либо строки соответствующих элементов какой-либо другой строки умноженных на некоторое число.
Чтобы решить систему линейных уравнений методом Гаусса, надо, применяя элементарные преобразования матриц, преобразовать матрицу  так, чтобы все элементы под главной диагональю были нулевыми.
так, чтобы все элементы под главной диагональю были нулевыми.
Пример 1. Решить систему уравнений  методом Крамера.
методом Крамера.
Решение. Найдем последовательно  .
.
 = -4 + 8 + 9 – 8 – 3 + 12 = 14,
= -4 + 8 + 9 – 8 – 3 + 12 = 14,
 = - 32 + 8 + 30 – 8 – 24 + 40 = 14,
= - 32 + 8 + 30 – 8 – 24 + 40 = 14,
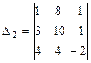 = -20 + 32 + 12 – 40 – 4 + 48 = 28,
= -20 + 32 + 12 – 40 – 4 + 48 = 28,
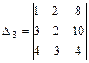 = 8 + 80 + 72 – 64 – 30 – 24 = 42.
= 8 + 80 + 72 – 64 – 30 – 24 = 42.
Получаем  .
.
Пример 2. Решить систему уравнений
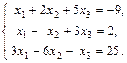 методом Гаусса.
методом Гаусса.
Решение. Запишем расширенную матрицу 
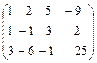 .
.
Сначала получим нули под главной диагональю в первом столбце  . Для этого из 2-й строки вычтем 1-ю, затем из 3-й строки вычтем 1-ю, умноженную на 3:
. Для этого из 2-й строки вычтем 1-ю, затем из 3-й строки вычтем 1-ю, умноженную на 3: 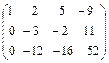 .
.
Получим нули под главной диагональю во втором столбце  . Для этого из 3-й строки вычитаем 2-ю строку, умноженную на 4:
. Для этого из 3-й строки вычитаем 2-ю строку, умноженную на 4:  . Последней матрице соответствует система уравнений:
. Последней матрице соответствует система уравнений:
 , которая решается элементарно методом последова-
, которая решается элементарно методом последова-
тельных исключений: сначала из 3-го уравнения определяется 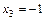 , затем из 2-го -
, затем из 2-го -  , затем из 1-го -
, затем из 1-го - 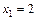 .
.
Упражнения:
1. Решить системы уравнений с помощью правила Крамера:
а)  ; б)
; б)  ;
;
в)  ; г)
; г) 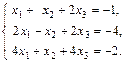 .
.
2. Решить системы уравнений методом Гаусса:
а)  ; б)
; б) 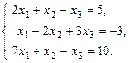 ;
;
в)  .
.
Векторы
Вектор – это отрезок, имеющий определенную длину и направление. Если А – начало вектора, В – его конец, то вектор обозначается символом  или
или  .
.
Длиной или модулем вектора  называется длина отрезка и обозначается
называется длина отрезка и обозначается 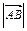 или
или  . Вектор, длина которого равна нулю, называется нулевым вектором и обозначается
. Вектор, длина которого равна нулю, называется нулевым вектором и обозначается  . Вектор, длина которого равна единице, называется единичным вектором и обозначается через
. Вектор, длина которого равна единице, называется единичным вектором и обозначается через 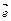 .
.
Векторы  и
и 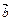 называются коллинеарными, если они лежат на одной прямой или на параллельных прямых.
называются коллинеарными, если они лежат на одной прямой или на параллельных прямых.
Три вектора в пространстве называются компланарными, если они лежат в одной плоскости или в параллельных плоскостях.
Вектор 
 , заданный в координатном пространстве Оxyz, может быть представлен в виде
, заданный в координатном пространстве Оxyz, может быть представлен в виде 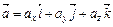 . Здесь
. Здесь 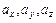 - проекции вектора
- проекции вектора  но соответствующие оси координат. Пишут
но соответствующие оси координат. Пишут  = (
= ( ).
).
Если  = (
= ( ),
), 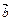 = (
= (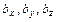 ), то
), то
1.  ;
;
2.  = (
= ( );
);
3.  ;
;
4.  =
= 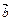
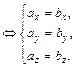
5. Вектор  коллинеарен вектору
коллинеарен вектору 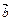 тогда и только тогда, когда выполняется условие
тогда и только тогда, когда выполняется условие 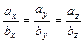 .
.
Если известны координаты точек  , то
, то  .
.
Пример 1. В Δ АВС сторона АВ точками M и N разделена на три равные части: 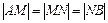 . Найти вектор
. Найти вектор 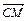 , если
, если  .
.
Решение.
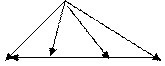 Имеем
Имеем 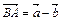 . Тогда
. Тогда  .
.
Получаем 
Пример 2. Даны координаты вершин Δ АВС: А (1;2;3), В (3;2;1), С (1;4;1). Показать, что Δ АВС – равносторонний.
Решение. Найдем координаты векторов  ,
, 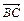 ,
,  . Получим
. Получим
 = (3-1, 2-2, 1-3) = (2, 0, -2),
= (3-1, 2-2, 1-3) = (2, 0, -2), 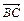 = (-2, 2, 0),
= (-2, 2, 0),  = (0, 2, -2). Вычислим длины данных векторов. Имеем
= (0, 2, -2). Вычислим длины данных векторов. Имеем 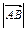 =
=  ,
, 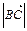 =
=  ,
,  =
=  . Так как
. Так как 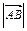 =
= 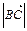 =
=  , то Δ АВС – равносторонний.
, то Δ АВС – равносторонний.
Пример 3. Вычислить длины медиан Δ АВС, если известны координаты его вершин: А (3;-2), В (5;2), С (-1;4).
Решение.
 |
Пусть А 1(x;y) – середина стороны ВС. Найдем ее координаты. Получим  , т.е. А 1(2;3). Координаты вектора
, т.е. А 1(2;3). Координаты вектора 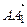 =(-1,5). Тогда
=(-1,5). Тогда 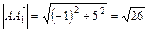 . Аналогично находятся длины остальных медиан.
. Аналогично находятся длины остальных медиан.
Упражнения:
1. Дан вектор  . Найти координаты вектора
. Найти координаты вектора  , если
, если  .
.
2. Дано 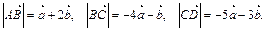 Доказать, что АВСD – трапеция.
Доказать, что АВСD – трапеция.
3. Векторы  служат диагоналями параллелограмма АВСD. Выразить векторы
служат диагоналями параллелограмма АВСD. Выразить векторы 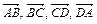 через векторы
через векторы  и
и 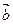 .
.
4. В Δ АВС дано  , точка М – середина стороны ВС. Выразить вектор
, точка М – середина стороны ВС. Выразить вектор  через векторы
через векторы  и
и  .
.
5. В Δ АВС проведены медианы 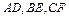 . Представить векторы
. Представить векторы  через векторы
через векторы 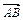 и
и  . Найти сумму векторов
. Найти сумму векторов  .
.