Уравнение
Ах + Ву + Сz + D = 0 (1)
(где А,В,C и D – постоянные коэффициенты, причем А2 + В2 +C2¹ 0) называется общим уравнением плоскости. Вектор 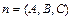 называется нормальным вектором плоскости.
называется нормальным вектором плоскости.
Если D ≠ 0, то разделив все члены уравнения (1) на (– D), получим уравнение плоскости в отрезках
 ,
,  (2)
(2)
где 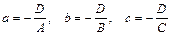 есть соответственно абсцисса, ордината и аппликата точек пересечения плоскости с осями Ох, Оу,Оz.
есть соответственно абсцисса, ордината и аппликата точек пересечения плоскости с осями Ох, Оу,Оz.
Уравнение плоскости, проходящей через точку М0(х0,у0,z0) и перпендикулярной вектору 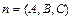 , имеет вид
, имеет вид
А(х-х0) + В(у-у0) + С(z-z0) = 0. (3)
Уравнение плоскости, проходящей через три заданные точки М1(х1,у1,z1), М2(х2,у2,z2), М3(х3,у3,z3) имеет вид
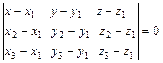 . (4)
. (4)
Угол между плоскостями А1 х + В1 у + С1 z + D1 = 0 и А2 х + В2 у + + С2 z +D2 = 0 определяется по формуле
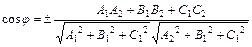 . (5)
. (5)
Условие параллельности плоскостей:
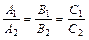 . (6)
. (6)
Условие перпендикулярности плоскостей:
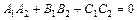 . (7)
. (7)
Расстояние от точкиМ0(х0,у0,z0) до плоскости, определяемой уравнением Ах + Ву + Сz + D = 0, находится по формуле
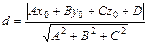 . (8)
. (8)
Пример 1. Составить уравнение плоскости, проходящей через точку А (5;4;3) и отсекающей равные отрезки на осях координат.
Решение. Используя уравнение (2) плоскости в отрезках, в котором а=в=с, имеем 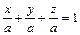 . Координаты точки А удовлетворяют уравнению искомой плоскости, поэтому выполняется равенство
. Координаты точки А удовлетворяют уравнению искомой плоскости, поэтому выполняется равенство 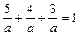 , откуда а = 12. итак, получаем уравнение x + y + z - 12 = 0.
, откуда а = 12. итак, получаем уравнение x + y + z - 12 = 0.
Пример 2. Найти уравнение плоскости, проходящей через точки А (2;-1;4) и В (3; 2; -1) перпендикулярно плоскости x + y + 2 z - 3 = 0.
Решение. В качестве нормального вектора 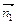 искомой плоскости можно взять вектор, перпендикулярный вектору
искомой плоскости можно взять вектор, перпендикулярный вектору 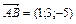 и нормальному вектору
и нормальному вектору 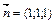 данной плоскости. Поэтому за
данной плоскости. Поэтому за 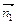 примем векторное произведение
примем векторное произведение 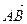 и
и 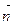 :
:
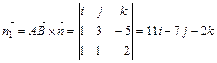 .
.
Остается воспользоваться уравнением плоскости (3), проходящей через данную точку (например, А) перпендикулярно заданному вектору 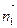 =(11; -7; -2):
=(11; -7; -2):
11(х -2) –7(у +1) –2(z -4) = 0, или 11 x - 7 y - 2 z - 21 = 0.
Уравнение прямой, проходящей через две точки М1(х1,у1,z1) и М2(х2,у2,z2), имеет вид
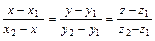 . (9)
. (9)
Уравнение прямой проходящей через точку М1(х1,у1,z1) параллельно направляющему вектору 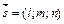 имеет вид
имеет вид
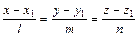 . (10)
. (10)
Уравнение (10) называется каноническим уравнением прямой. Из уравнения (10), введя параметр t, нетрудно перейти к параметрическим уравнениям:
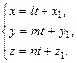 (11)
(11)
Угол между двумя прямыми, заданными их каноническими уравнениями 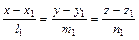 и
и 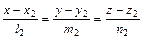 , определяется по формуле
, определяется по формуле
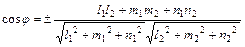 ; (12)
; (12)
условие параллельности двух прямых:
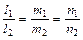 ; (13)
; (13)
условие перпендикулярности двух прямых:
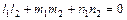 . (14)
. (14)
Угол между прямой 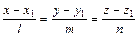 и плоскостью Ах + Ву + Сz + + D = 0определяется по формуле
и плоскостью Ах + Ву + Сz + + D = 0определяется по формуле

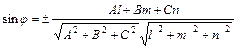 ; (15)
; (15)
условие параллельности прямой и плоскости:
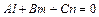 ; (16)
; (16)
условие перпендикулярности прямой и плоскости:
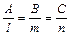 . (17)
. (17)
Пример 3. Из начала координат опустить перпендикуляр на прямую 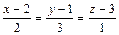 .
.
Решение. Используя условие (17) перпендикулярности прямой и плоскости и полагая A=l, B=m, C=n, D=0, составим уравнение плоскости, проходящей через начало координат и перпендикулярной заданной прямой. Это уравнение имеет вид 2 х +3 у + z =0.
Найдем точку пересечения этой плоскости и данной прямой. Параметрические уравнения прямой запишутся так: x =2 t +2, y =3 t +1, z = t +3. Для определения t имеем уравнение 2(2 t +3)+3(3 t +1)+ t +3=0, откуда 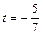 . Координаты точки пересечения
. Координаты точки пересечения 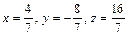 , т.е.
, т.е. 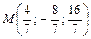 .
.
Остается составить уравнение прямой, проходящей через точку М; используя соотношение (9), получим 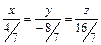 , или
, или 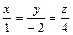 .
.
Пример 4. Составить уравнение прямой, проходящей через точку М (1;1;1) и перпендикулярной векторам s1 = 2 i + 3 j + k и s2 = 3 i + j + 2 k.
Решение. Данная прямая параллельна вектору s1 ´ s2 = 5 i – j - 7 k, поэтому она определяется уравнением 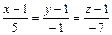 .
.
Упражнения:
1. Написать уравнение плоскости, проходящей через заданные точки М1 и М2 перпендикулярно заданной плоскости Q:
а) Q: - x + y – 1 = 0, M 1(1, 2, 0), M 2(2, 1, 1);
б) Q: 2 x – y + z + 1 = 0, M 1(0, 1, 1), M 2(2, 0, 1).
2. Написать уравнение плоскости, проходящей через заданные точки М 1, М 2, М 3, если:
а) М 1(1, 2, 0), М 2(2, 1, 1), М 3(3, 0, 1);
б) М 1(1, 1,1), М 2(0, -1, 2), М 3(2, 3, -1).
3. Вычислить углы между следующими плоскостями:
а) 4 x – 5 y + 3 z - 1 = 0 и x – 4 y - z + 9 = 0;
б) 3 x – y + 2 z + 15 = 0 и 5 x + 9 y - 3 z - 1 = 0;
в) 6 x + 2 y - 4 z + 17 = 0 и 9 x + 3 y - 6 z - 4 = 0.
4. Вычислить расстояние:
а) точки (3; 1; -1) от плоскости 22 x + 4 y - 20 z - 45 = 0,
б) точки (4; 3; -2) от плоскости 3 x – y + 5 z + 1 = 0.
5. Написать уравнение прямой, проходящей через две заданные точки М 1 и М 2, если:
а) М 1(1, -2, 1), М 2(3, 1, -1);
б) М 1(3, -1, 0), М 2(1, 0, -3).
6. Прямая задана общими уравнениями. Написать канонические уравнения данных прямых, если:
а) 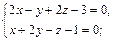 б)
б) 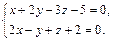
7. Даны три последовательные вершины параллелограмма: А (3; 0; -1), В (1; 2; -4) и С (0; 7; -2). Найти уравнения сторон АD и CD.