Заданий движения точки
Рассмотрим движение точки в плоскости. Уравнения движение точки заданы координатным способом
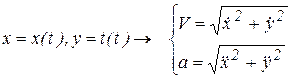 .
.
Уравнение движения точки, заданной в естественной форме связано с координатным способом соотношением
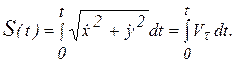
Скорость при естественном задании тогда равна
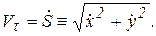
Для касательной составляющей ускорения имеем
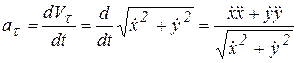 .
.
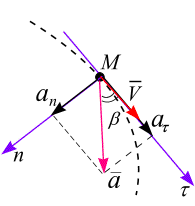
Нормальная составляющая ускорения 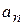 связана с модулем ускорения
связана с модулем ускорения  и углом
и углом 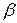 (угол
(угол 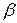 – угол между вектором ускорения
– угол между вектором ускорения 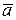 и вектором скорости
и вектором скорости 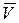 , рис. 3..10, соотношением:
, рис. 3..10, соотношением:
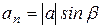 .
.
Модуль векторного произведения векторов 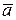 и
и 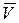
Рис. 3.10 также связывает  ,
, 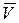 и углом
и углом 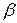 :
:
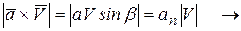
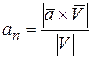 .
.
Тогда:
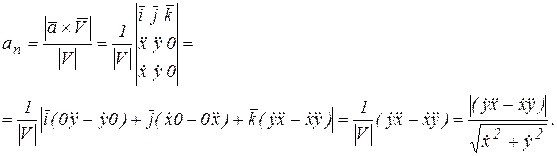
Связь координатного и естественного способов заданий движения точки
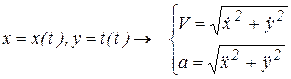 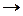 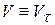 , , 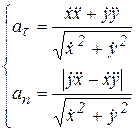
|
Пример 3.1. Движение точки в плоскости  задано координатным способом уравнениями
задано координатным способом уравнениями 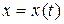 ,
, 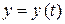 :
:
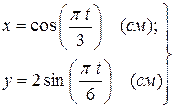
| (а) |
| (б) |
где 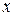 и
и 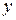 выражены в см,
выражены в см, 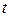 - в с.
- в с.
Требуется задать движение точки в явном виде; вычислить скорость, нормальную и касательную составляющие ускорения, радиус кривизны траектории в соответствующей точке для момента времени 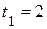 с.
с.
Решение. Дляпостроения траектории в декартовой системе координат определим область значений 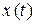 и
и 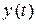 . Функции
. Функции 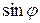 и
и 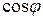 - ограничены, тогда область значений
- ограничены, тогда область значений 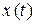 и
и 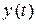 определяется неравенствами:
определяется неравенствами:
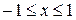 ;
; 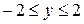 .
.
Получим зависимость 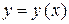 . Для этого из (а)–(б) исключим параметр
. Для этого из (а)–(б) исключим параметр  . Введём обозначение
. Введём обозначение 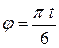 , тогда уравнения (а) и (б) перепишутся в виде:
, тогда уравнения (а) и (б) перепишутся в виде:
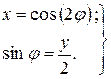
Распишем первое уравнение полученной системы, используя формулу двойного угла (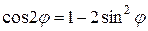 ), приведем подобные члены и выразим
), приведем подобные члены и выразим 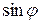 через
через 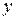 :
:
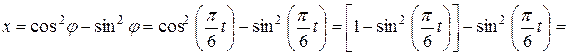
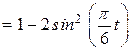 .
.
Из второго уравнения выразим 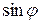 через
через 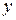 , получим:
, получим:
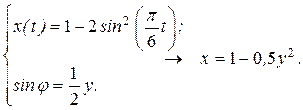 (с)
(с)
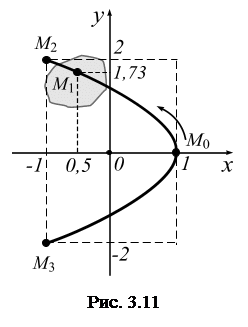 Итак, траекторией точки является парабола с координатой вершины
Итак, траекторией точки является парабола с координатой вершины 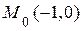 , ветви параболы вытянуты вдоль оси
, ветви параболы вытянуты вдоль оси 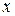 слева от вершины (рис. 3.11).
слева от вершины (рис. 3.11).
При 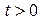 функция
функция 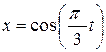 убывает, а
убывает, а 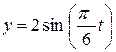 - возрастает (рис.1.18); следовательно, точка из положения
- возрастает (рис.1.18); следовательно, точка из положения 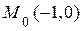 начинает движение по верхней ветви параболы до точки
начинает движение по верхней ветви параболы до точки 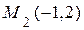 , далее точка движется обратно по верхней ветви траектории и через точку с координатами
, далее точка движется обратно по верхней ветви траектории и через точку с координатами 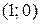 движется по нижней ветви параболы до точки
движется по нижней ветви параболы до точки 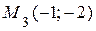 – и т.д.
– и т.д.
В целом точка М совершает колебательные движения по построенной параболе в ограниченной пунктиром области. Направление движения в первые 2 с указано стрелкой на рис. 3.11.
Вычислим положение точки 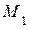 на траектории при
на траектории при 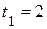 с:
с:
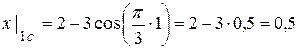 (см);
(см);
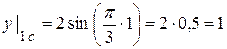 (см).
(см).
2.Вычислим скорость точки 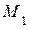 при
при 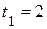 с.
с.
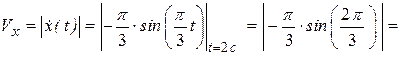
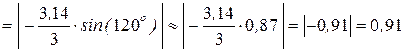 (см/с);
(см/с);
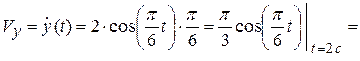
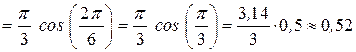 (см/с);
(см/с);
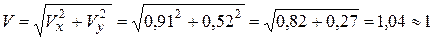 (см/с).
(см/с).
Cправка. Формулы приведения:
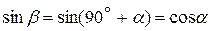 ; ; 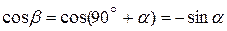 . .
|
Значения 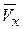 и
и 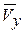 отложим в масштабе на графике (рис. 3.12, а).
отложим в масштабе на графике (рис. 3.12, а).
| а | 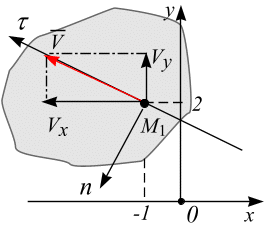
| б | 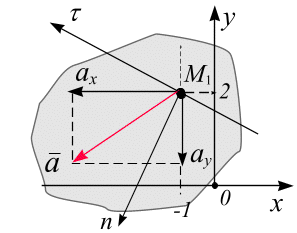
|
Рис. 3.12
Вектор скорости точки  является диагональю параллелограмма, достроенного на этих векторах, и определяет направление движения точки, а также определяет направление и положение касательной оси
является диагональю параллелограмма, достроенного на этих векторах, и определяет направление движения точки, а также определяет направление и положение касательной оси  .
.
Вычислим ускорение точки  при
при 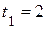 с:
с:
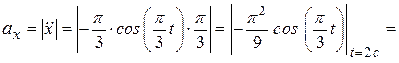
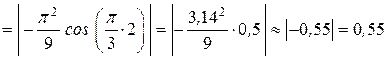 (см/с2);
(см/с2);
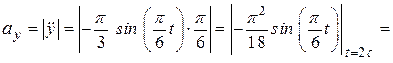
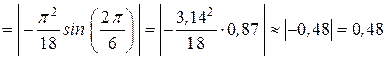 (см/с2);
(см/с2);
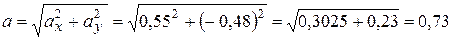 (см/с2).
(см/с2).
Вектор ускорения точки 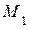 –
– 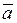 - получаем построением параллелограмма на проекциях ускорений
- получаем построением параллелограмма на проекциях ускорений 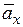 и
и 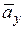 в выбранном масштабе (рис. 3.12, б).
в выбранном масштабе (рис. 3.12, б).
Как видно из рис. 3.12, в вектор полного ускорения точки 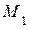 направлен внутрь вогнутости траектории движения точки.
направлен внутрь вогнутости траектории движения точки.
Касательная и нормальная составляющие ускорения точки (рис. 3.13). При координатном способе задания движения указанные составляющие ускорения рассчитываются по формулам:
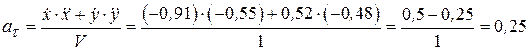 (см/с2);
(см/с2);
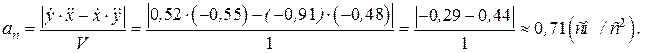
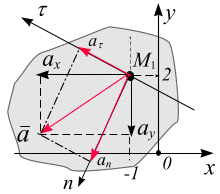 Рис. 3.13
Рис. 3.13
| Касательное и нормальное ускорения точки можно вычислить геометрически. Для этого в точке  необходимо построить оси естественного трехгранника необходимо построить оси естественного трехгранника  и и 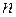 . Положение и направление оси . Положение и направление оси 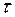 определили ранее - по построенному вектору скорости точки определили ранее - по построенному вектору скорости точки 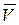 .
Перпендикулярно этой оси, в сторону .
Перпендикулярно этой оси, в сторону
|
вогнутости траектории, проведём главную нормаль 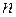 (полуось). Отложим в масштабе проекции
(полуось). Отложим в масштабе проекции 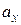 и
и 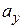 и построим вектор
и построим вектор 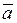 (рис. 3.13). Проекция вектора ускорения
(рис. 3.13). Проекция вектора ускорения 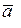 на ось
на ось 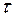 будет соответствовать касательной составляющей ускорения
будет соответствовать касательной составляющей ускорения 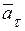 . Измеряя длину указанного вектора и умножая на масштаб, получим значение
. Измеряя длину указанного вектора и умножая на масштаб, получим значение 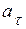 ; в данном случае
; в данном случае 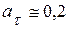 (см/с2). Вектор
(см/с2). Вектор 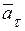 совпадает по направлению с вектором скорости точки
совпадает по направлению с вектором скорости точки 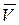 , следовательно, движение точки по параболе в данный момент времени – ускоренное.
, следовательно, движение точки по параболе в данный момент времени – ускоренное.
Соответственно, проекция 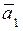 на ось
на ось 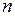 будет определять нормальное ускорение
будет определять нормальное ускорение 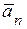 . Измеряя длину полученной проекции и умножая на масштаб, получим значение
. Измеряя длину полученной проекции и умножая на масштаб, получим значение 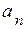 ; в данном случае
; в данном случае 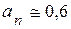 (см/с2).
(см/с2).
Получено достаточно хорошее соответствие значений 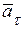 и
и 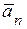 , рассчитанных разными способами.
, рассчитанных разными способами.
Радиус кривизны траектории.
Имеем:
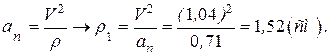
Вычислим уравнение движения точки 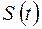 , заданное естественном способом.
, заданное естественном способом.
Имеем:
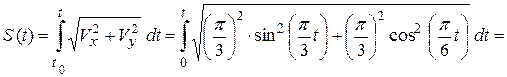
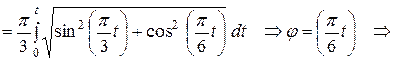
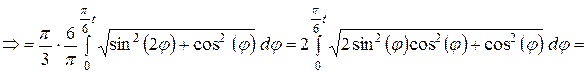
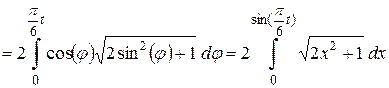 .
.
Получили уравнение движения точки, заданное естественным способом в интегральном виде.