Обозначим через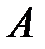 
– матрицу, элементы которой являются коэффициентами при неизвестных;
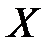– матрицу-столбец неизвестных; 
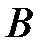– матрицу-столбец свободных членов:
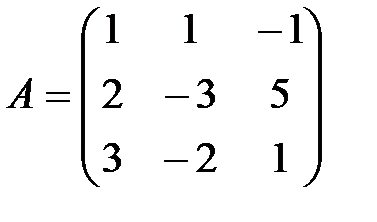
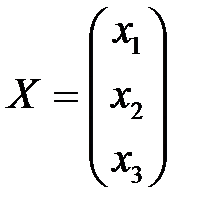
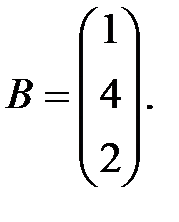
С учетом этих обозначений данная система уравнений принимает следующую матричную форму: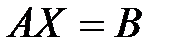 
.
Если матрица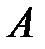 
– невырожденная (определитель матрицы отличен от нуля), то она имеет обратную матрицу 
.
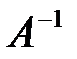Умножив обе части уравнения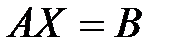 
на матрицу 
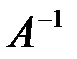справа, получим: 
.
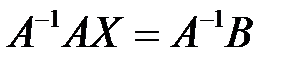Учитывая, что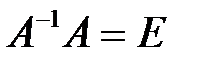 
и 
, и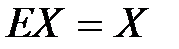меем
.
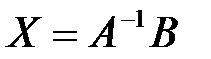Это равенство называется матричной записью решения системы линейных уравнений. Для нахождения решения системы уравнений необходимо вычислить обратную матрицу.
Система будет иметь решение, если определитель матрицы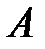 
отличен от нуля.
В нашем случае определитель матрицы совпадает с главным определителем системы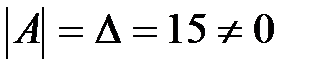 
, а значит, матрица невырожденная и имеет обратную матрицу.
Найдем обратную матрицу через алгебраические дополнения.
Пусть имеем невырожденную матрицу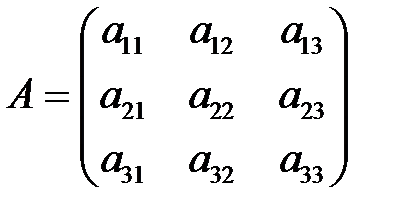 
.
Тогда:
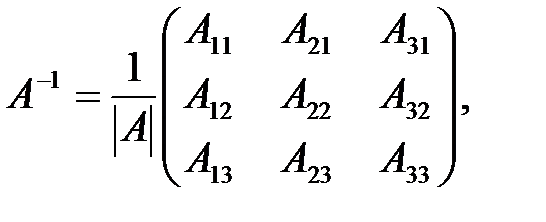где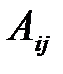 
– алгебраическое дополнение элемента 
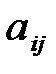в определителе матрицы А.
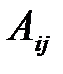определяется формулой: 
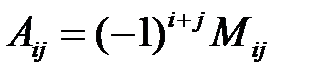, где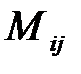 
– минор (определитель) 
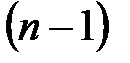-го порядка, полученный вычеркиванием i- й строки и j- го столбца в определителе матрицы А.
Вычисляем алгебраические дополнения.
| 
|
| 
|
| 
|
| 
|
|
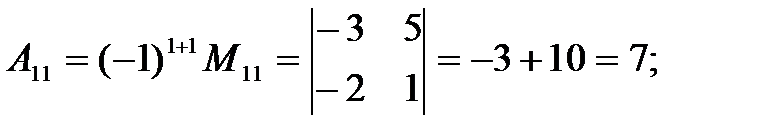
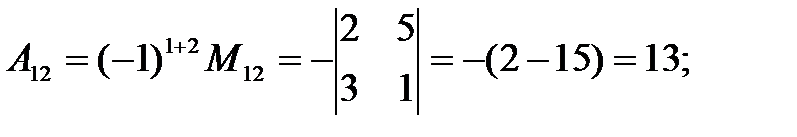
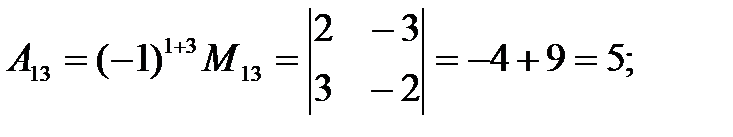
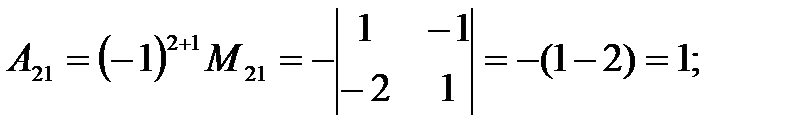
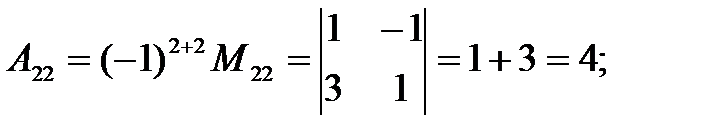
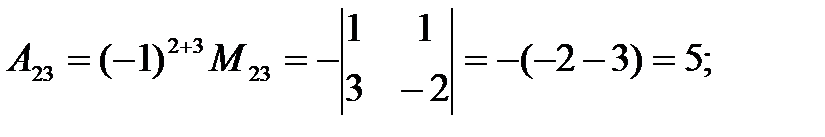
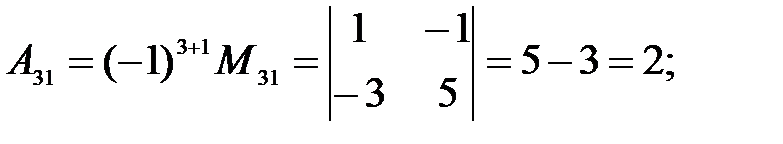
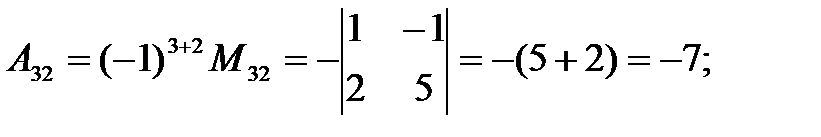
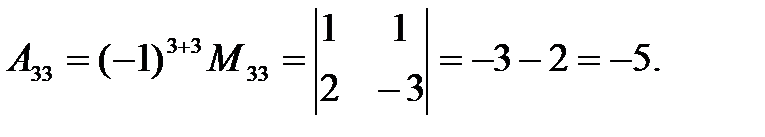
Транспонируя полученные алгебраические дополнения, составим присоединенную матрицу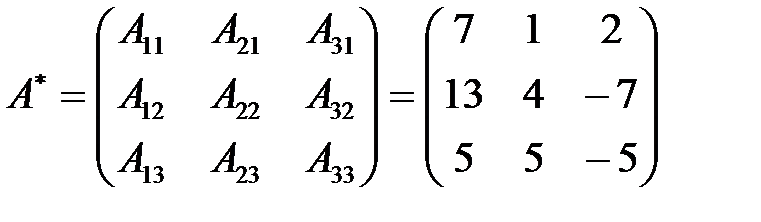 
Находим обратную матрицу: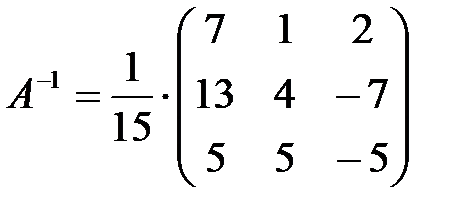 
.
Тогда,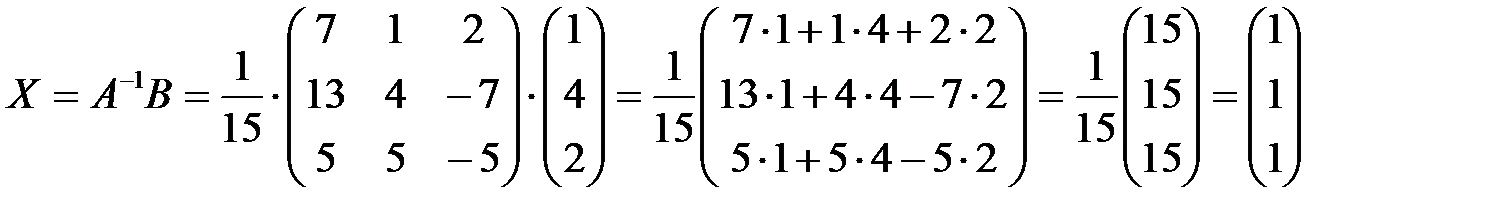 
.
Ответ: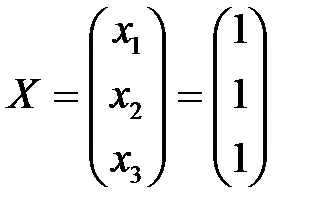 
.
#
в) Метод Жордана-Гаусса.
Запишем расширенную матрицу системы:
.
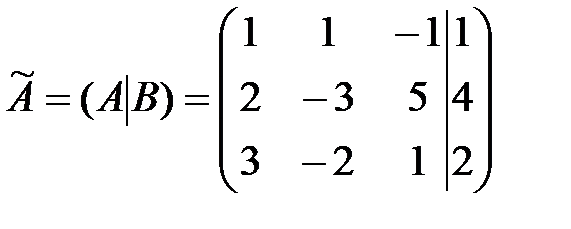Идея метода заключается в переходе от расширенной матрицы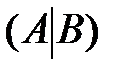 
к матрице вида 
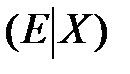, то есть, используя элементарные преобразования со строками расширенной матрицы, получаем на месте матрицы 
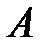единичную матрицу 
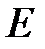, при этом на месте матрицы 
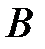получим матрицу неизвестных 
.
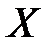Итак:
Переход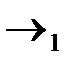 
: получаем нули в первом столбце (вводим переменную 
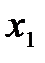в базис).
К элементам второй строки прибавляем элементы первой строки, умноженные на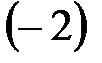 
, к элементам третьей строки прибавляем элементы первой строки, умноженные на 
;
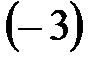Переход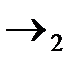 
: элементы третьей строки умножаем на (2) и вычитаем из них элементы второй строки, чтобы получить единицу в третьей строке третьего столбца;
Переход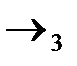 
: получаем нули в третьем столбце (вводим переменную 
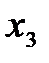в базис).
К элементам второй строки прибавляем элементы третьей строки, умноженные на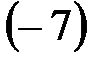 
, к элементам первой строки прибавляем элементы третьей строки;
Переход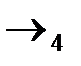 
: делим элементы второй строки на 30, чтобы получить единицу во второй строке второго столбца;
Переход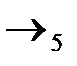 
: получаем нули во втором столбце (вводим переменную 
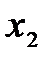в базис).
К элементам первой строки прибавляем элементы второй строки, умноженные на (4), к элементам третьей строки прибавляем элементы второй строки, умноженные на (5).
Имеем: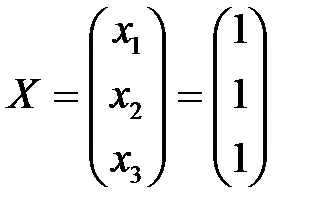
.
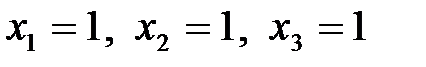Ответ: .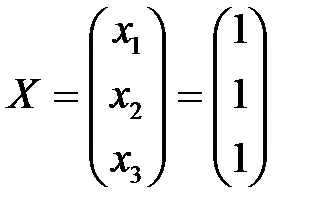
Задание 2.1. Найти объем треугольной пирамиды и длину высоты, опущенной из вершины А на грань BCD, если вершины имеют координаты A (0; 0; 1), B (2; 3; 5), C (6; 2; 3), D (3; 7; 2).
Решение. Найдем координаты векторов, на которых построена пирамида.
.
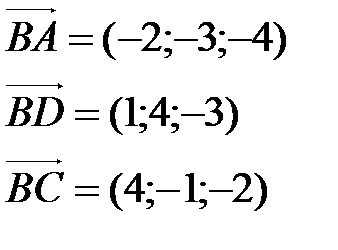Тогда объем пирамиды
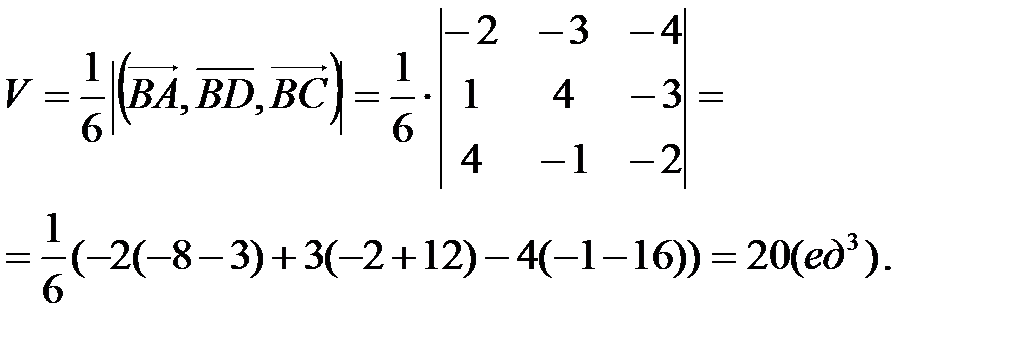
Для нахождения длины высоты пирамиды найдем сначала площадь основания BCD. В основании пирамиды лежит треугольник BCD, площадь которого численно равна половине площади параллелограмма, построенного на векторах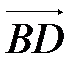 
и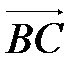 
. Площадь параллелограмма определяется как модуль векторного произведения.
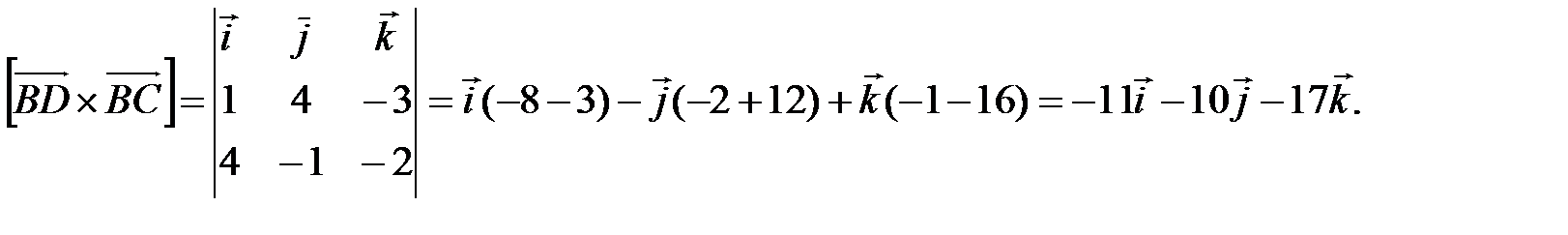
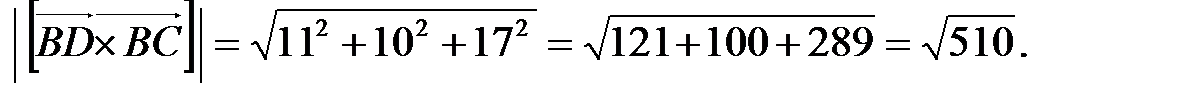
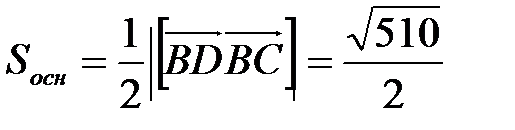(ед2).
Т.к.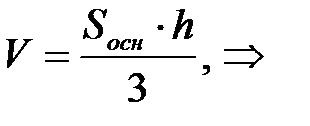 
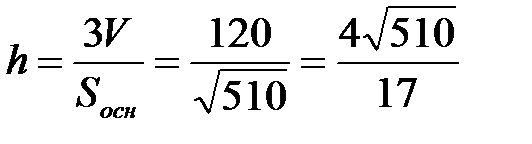(ед).
Ответ: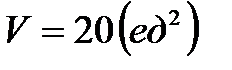 
, 
.
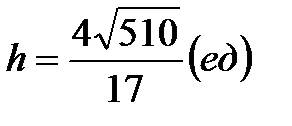Задание 2.2. Построить кривую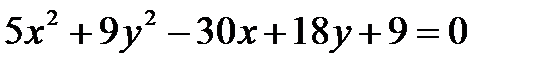 
. Указать координаты нового центра системы координат, полуоси кривой.
Решение. Выделим в уравнении полные квадраты по х и у:
,
.
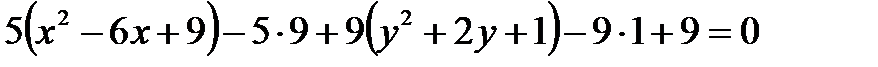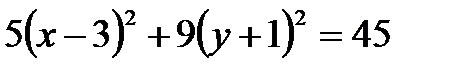Разделим обе части на свободный член: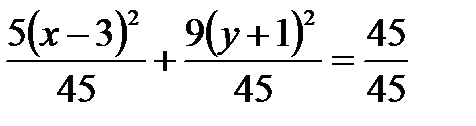 
.
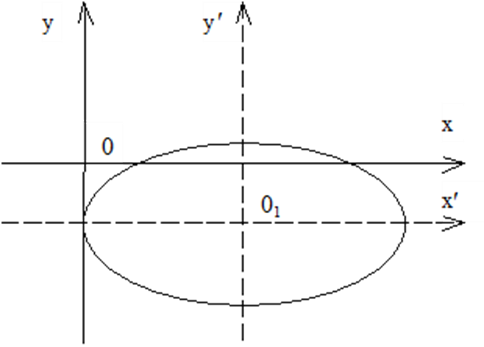
Получим уравнение эллипса со смещенным центром:
.
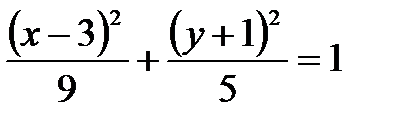Теперь используем формулы параллельного переноса координатных осей:
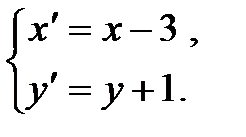
Получим каноническое уравнение эллипса в новой системе координат:
.
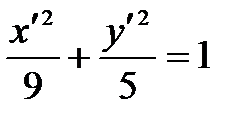Центр новой системы координат: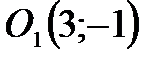 
, полуоси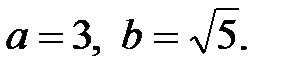 
Задание 3.1. Исследовать функцию на непрерывность и определить тип точек разрыва, если они есть.
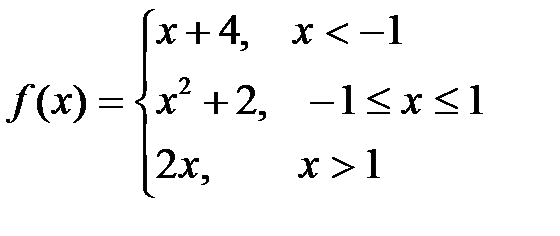
Решение. Так как функция определена при всех значениях аргумента и состоит из нескольких аналитических выражений, представляющих собой многочлены (непрерывные функции), то для исследования достаточно рассмотреть, так называемые точки стыка, то есть точки, при переходе через которые функция меняет одно аналитическое выражение на другое.
Для исследования нам необходимо найти значение функции и односторонние пределы в этих точках.
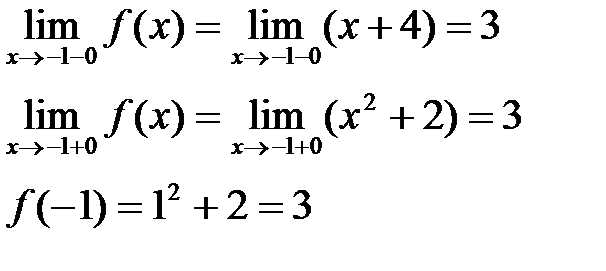
Следовательно,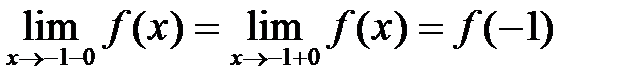 
, а значит, в точке 
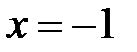функция непрерывна.
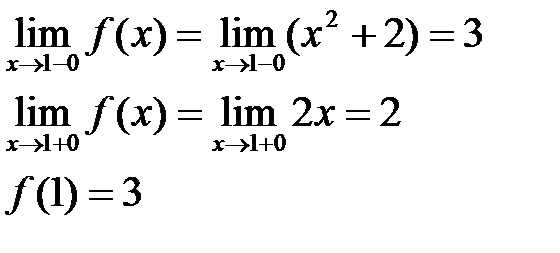
Точка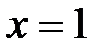 
является точкой разрыва первого рода, типа скачок, так как односторонние пределы различны 
.
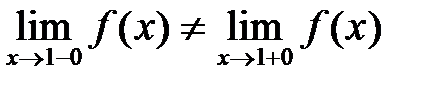у
-4 -1 0 1 х
Задание 3.2.
Исследовать функцию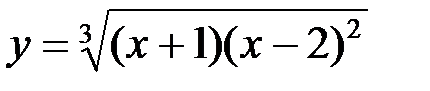 
и построить ее график.
При выполнении данного задания используем схему, указанную ниже.