Дробно-рациональная функция

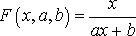
. (27)

Перепишем (27) следующим образом:

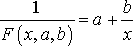
. (28)

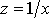
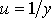
Из (28) видно, что задача сводится к задаче, рассмотренной в предыдущем пункте. Действительно, если в исходной таблице заменить значения x, y их обратными величинами по формулам , и искать для новой таблицы приближающую функцию вида 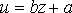, то найденные значения будут искомыми для функции (27).

Аппроксимация линейной комбинацией функций

Будем искать аппроксимирующую функцию 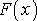в виде линейной комбинации известных функций , , :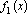

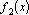
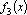
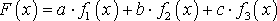
. (29)

Подставив (29) в (8) и выполнив очевидные алгебраические преобразования, получаем систему линейных уравнений, относительно неизвестных коэффициентов a, b, c:

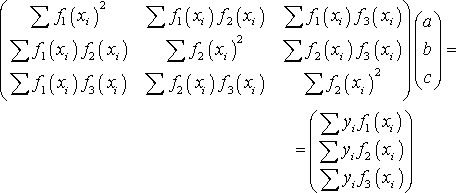
(30)

Решив систему линейных уравнений (30) любым известным способом, находим значение коэффициентов a, b, c и тем самым аналитическое выражение для аппроксимирующей функции.

Аппроксимация функцией произвольного вида

Для решения задачи обобщенной нелинейной регрессии в пакете MATLAB имеется функция lsqnonlin(), возвращающая решение задачи нахождения точки минимума функции f (x)

,

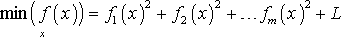
где в общем случае f (x) −вектор-функция, x − вектор-столбец искомых переменных, L − некоторая константа.

Синтаксис функции lsqnonlin():

x = lsqnonlin(fun,x0)

...

 

аналогичен синтаксису функции fsolve(), обсуждавшемся нами в ранее. Поэтому далее мы ограничимся только примером, демонстрирующим использование данной функции для нахождения параметров функции

.

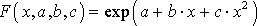
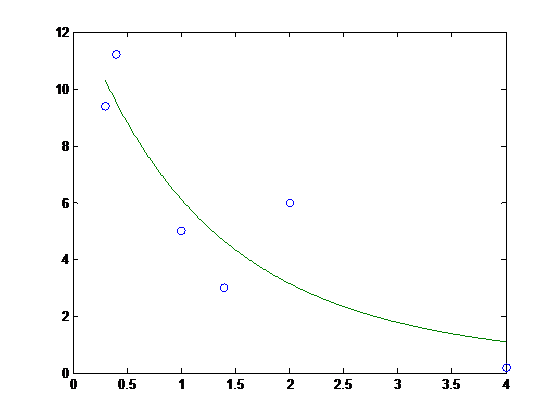
Для решения данной задачи в пакете MATLAB необходимо выполнить следующую последовательность действий:

 

1. Создать m - файл функцию F.m

 

function z=F(c,x,y)

z=y-exp(c(1)+c(2)*x+c(3)*x.^2);

end

 

2. Создать m - файл сценарий

 

% задание исходных данных

x=[0.3;0.4;1;1.4;2;4]

y=[9.4;11.2;5;3;6;0.2]

z=[1 0 -1] % начальное приближения

% вычисление коэффициентов аппроксимирующей функции

c = lsqnonlin('F',z',[],[],[],x,y)

% задание аппроксимирующей функции

f=inline('exp(a+b*x+c*x.^2)','x','a','b','c');

% координаты, в которых будут вычисляться значения аппр. функции

X=x(1):0.01:x(end);

% вычисление значений аппроксимирующей функции

Y=f(X,c(1),c(2),c(3));

Plot(x,y,'o',X,Y)

 

c =

2.5696

-0.8037

0.0462

Математическая оптимизация и ее методы

Оптимизация — в математике, информатике и исследовании операций задача нахождения экстремума (минимума или максимума) целевой функции в некоторой области конечномерного векторного пространства, ограниченной набором линейных и/или нелинейных равенств и/или неравенств.

Теорию и методы решения задачи оптимизации изучает математическое программирование.

Математическое программирование — это область математики, разрабатывающая теорию, численные методы решения многомерных задач с ограничениями. В отличие от классической математики, математическое программирование занимается математическими методами решения задач нахождения наилучших вариантов из всех возможных.

В процессе проектирования ставится обычно задача определения наилучших, в некотором смысле, структуры или значений параметров объектов. Такая задача называется оптимизационной. Если оптимизация связана с расчётом оптимальных значений параметров при заданной структуре объекта, то она называется параметрической оптимизацией. Задача выбора оптимальной структуры является структурной оптимизацией.

Стандартная математическая задача оптимизации формулируется таким образом. Среди элементов χ, образующих множества Χ, найти такой элемент χ^*, который доставляет минимальное значение f(χ^*) заданной функции f(χ). Для того, чтобы корректно поставить задачу оптимизации, необходимо задать:

1. Допустимое множество — множество X = { x → | g i (x →) ≤ 0, i = 1, …, m } ⊂ R n {\displaystyle \mathbb {X} =\{{\vec {x}}|\;g_{i}({\vec {x}})\leq 0,\;i=1,\ldots,m\}\subset \mathbb {R} ^{n}};

2. Целевую функцию — отображение 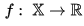f: X → R {\displaystyle f:\;\mathbb {X} \to \mathbb {R} };

3. Критерий поиска (max или min).

Тогда решить задачу 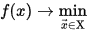f (x) → min x → ∈ X {\displaystyle f(x)\to \min _{{\vec {x}}\in \mathrm {X} }} означает одно из:

1. Показать, что 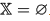X = ∅ {\displaystyle \mathbb {X} =\varnothing }

2. Показать, что целевая функция 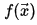f (x →) {\displaystyle f({\vec {x}})} не ограничена снизу.

3. Найти 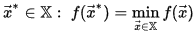x → ∗ ∈ X: f (x → ∗) = min x → ∈ X f (x →) {\displaystyle {\vec {x}}^{*}\in \mathbb {X}:\;f({\vec {x}}^{*})=\min _{{\vec {x}}\in \mathbb {X} }f({\vec {x}})}.

4. Если 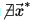∄ x → ∗ {\displaystyle \nexists {\vec {x}}^{*}}, то найти 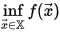inf x → ∈ X f (x →) {\displaystyle \inf _{{\vec {x}}\in \mathbb {X} }f({\vec {x}})}.

Если минимизируемая функция не является выпуклой, то часто ограничиваются поиском локальных минимумов и максимумов: точек 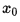x 0 {\displaystyle x_{0}} таких, что всюду в некоторой их окрестности 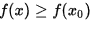f (x) ≥ f (x 0) {\displaystyle f(x)\geq f(x_{0})} для минимума и 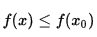f (x) ≤ f (x 0) {\displaystyle f(x)\leq f(x_{0})} для максимума.

Если допустимое множество 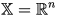X = R n {\displaystyle \mathbb {X} =\mathbb {R} ^{n}}, то такая задача называется задачей безусловной оптимизации, в противном случае — задачей условной оптимизации.

Задачи линейного программирования были первыми подробно изученными задачами поиска экстремума функций при наличии ограничений типа неравенств. В 1820 году Фурье и затем в 1947 году Данциг предложил метод направленного перебора смежных вершин в направлении возрастания целевой функции — симплекс-метод, ставший основным при решении задач линейного программирования.

Присутствие в названии дисциплины термина «программирование» объясняется тем, что первые исследования и первые приложения линейных оптимизационных задач были в сфере экономики, так как в английском языке слово «programming» означает планирование, составление планов или программ. Вполне естественно, что терминология отражает тесную связь, существующую между математической постановкой задачи и её экономической интерпретацией (изучение оптимальной экономической программы). Термин «линейное программирование» был предложен Данцигом в 1949 году для изучения теоретических и алгоритмических задач, связанных с оптимизацией линейных функций при линейных ограничениях.

Поэтому наименование «математическое программирование» связано с тем, что целью решения задач является выбор оптимальной программы действий.

Выделение класса экстремальных задач, определяемых линейным функционалом на множестве, задаваемом линейными ограничениями, следует отнести к 1930-м годам. Одними из первых, исследовавшими в общей форме задачи линейного программирования, были: Джон фон Нейман — математик и физик, доказавший основную теорему о матричных играх и изучивший экономическую модель, носящую его имя, и Канторович — советский академик, лауреат Нобелевской премии (1975), сформулировавший ряд задач линейного программирования и предложивший в 1939 году метод их решения (метод разрешающих множителей), незначительно отличающийся от симплекс-метода.

В 1931 году венгерский математик Б. Эгервари рассмотрел математическую постановку и решил задачу линейного программирования, имеющую название «проблема выбора», метод решения получил название «венгерского метода».

Канторовичем совместно с М. К. Гавуриным в 1949 году разработан метод потенциалов, который применяется при решении транспортных задач. В последующих работах Канторовича, Немчинова, В. В. Новожилова, А. Л. Лурье, А. Брудно, Аганбегяна, Д. Б. Юдина, Е. Г. Гольштейна и других математиков и экономистов получили дальнейшее развитие как математическая теория линейного и нелинейного программирования, так и приложение её методов к исследованию различных экономических проблем.

Методам линейного программирования посвящено много работ зарубежных учёных. В 1941 году Ф. Л. Хитчкок поставил транспортную задачу. Основной метод решения задач линейного программирования — симплекс-метод — был опубликован в 1949 году Данцигом. Дальнейшее развитие методы линейного и нелинейного программирования получили в работах Куна, А. Таккера, Гасса, Чарнеса, Била и др.

Одновременно с развитием линейного программирования большое внимание уделялось задачам нелинейного программирования, в которых либо целевая функция, либо ограничения, либо то и другое нелинейны. В 1951 году была опубликована работа Куна и Таккера, в которой приведены необходимые и достаточные условия оптимальности для решения задач нелинейного программирования. Эта работа послужила основой для последующих исследований в этой области.

Начиная с 1955 году опубликовано много работ, посвященных квадратическому программированию (работы Била, Баранкина и Дорфмана, Франка и Вольфа, Марковица и др.). В работах Денниса, Розена и Зонтендейка разработаны градиентные методы решения задач нелинейного программирования.

В настоящее время для эффективного применения методов математического программирования и решения задач на компьютерах разработаны алгебраические языки моделирования, представителями которыми являются AMPL и LINGO.

Общая запись задач оптимизации задаёт большое разнообразие их классов. От класса задачи зависит подбор метода (эффективность её решения). Классификацию задач определяют: целевая функция и допустимая область (задаётся системой неравенств и равенств или более сложным алгоритмом).

Методы оптимизации классифицируют в соответствии с задачами оптимизации:

• Локальные методы: сходятся к какому-нибудь локальному экстремуму целевой функции. В случае унимодальной целевой функции, этот экстремум единственен, и будет глобальным максимумом/минимумом.
• Глобальные методы: имеют дело с многоэкстремальными целевыми функциями. При глобальном поиске основной задачей является выявление тенденций глобального поведения целевой функции.

Существующие в настоящее время методы поиска можно разбить на три большие группы:

1. детерминированные;

2. случайные (стохастические);

3. комбинированные.

По критерию размерности допустимого множества, методы оптимизации делят на методы одномерной оптимизации и методы многомерной оптимизации.

По виду целевой функции и допустимого множества, задачи оптимизации и методы их решения можно разделить на следующие классы:

• Задачи оптимизации, в которых целевая функция 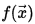f (x →) {\displaystyle f({\vec {x}})} и ограничения 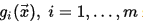g i (x →), i = 1, …, m {\displaystyle g_{i}({\vec {x}}),\;i=1,\ldots,m} являются линейными функциями, разрешаются так называемыми методами линейного программирования.
• В противном случае имеют дело с задачей нелинейного программирования и применяют соответствующие методы. В свою очередь из них выделяют две частные задачи:
• если 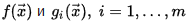f (x →) {\displaystyle f({\vec {x}})} g i (x →), i = 1, …, m {\displaystyle g_{i}({\vec {x}}),\;i=1,\ldots,m} — выпуклые функции, то такую задачу называют задачей выпуклого программирования;
• если 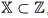X ⊂ Z {\displaystyle \mathbb {X} \subset \mathbb {Z} }, то имеют дело с задачей целочисленного (дискретного) программирования.

По требованиям к гладкости и наличию у целевой функции частных производных, их также можно разделить на:

• прямые методы, требующие только вычислений целевой функции в точках приближений;
• методы первого порядка: требуют вычисления первых частных производных функции;
• методы второго порядка: требуют вычисления вторых частных производных, то есть гессиана целевой функции.

Помимо того, оптимизационные методы делятся на следующие группы:

• аналитические методы (например, метод множителей Лагранжа и условия Каруша-Куна-Таккера);
• численные методы;
• графические методы.

В зависимости от природы множества X задачи математического программирования классифицируются как:

• задачи дискретного программирования (или комбинаторной оптимизации) — если X конечно или счётно;
• задачи целочисленного программирования — если X является подмножеством множества целых чисел;
• задачи нелинейного программирования, если ограничения или целевая функция содержат нелинейные функции и X является подмножеством конечномерного векторного пространства.
• Если же все ограничения и целевая функция содержат лишь линейные функции, то это — задача линейного программирования.

Кроме того, разделами математического программирования являются параметрическое программирование, динамическое программирование и стохастическое программирование.

Математическое программирование используется при решении оптимизационных задач исследования операций.

Способ нахождения экстремума полностью определяется классом задачи. Но перед тем, как получить математическую модель, нужно выполнить 4 этапа моделирования:

• Определение границ системы оптимизации
• Отбрасываем те связи объекта оптимизации с внешним миром, которые не могут сильно повлиять на результат оптимизации, а, точнее, те, без которых решение упрощается
• Выбор управляемых переменных
• «Замораживаем» значения некоторых переменных (неуправляемые переменные). Другие оставляем принимать любые значения из области допустимых решений (управляемые переменные)
• Определение ограничений на управляемые переменные
• … (равенства и/или неравенства)
• Выбор числового критерия оптимизации (например, показателя эффективности)
• Создаём целевую функцию

Метод Монте-Карло

Анализ риска — необъемлемая часть любого решения, которое мы принимаем. Мы постоянно сталкиваемся с неопределенностью, неоднозначностью и изменчивостью. И даже несмотря на беспрецедентно широкий доступ к информации, мы не можем точно предсказать будущее. Моделирование по методу Монте-Карло (также известное как метод Монте-Карло) позволяет рассмотреть все возможные последствия ваших решений и оценить воздействие риска, что обеспечивает более высокую эффективность принятия решений в условиях неопределенности.

Моделирование по методу Монте-Карло представляет собой автоматизированную математическую методику, предназначенную для учета риска в процессе количественного анализа и принятия решений. Эта методика применяется профессионалами в разных областях, таких как финансы, управление проектами, энергетика, производство, проектирование, НИОКР, страхование, нефтегазовая отрасль, транспорт и охрана окружающей среды.

Каждый раз в процессе выбора направления дальнейших действий моделирование по методу Монте-Карло позволяет специалисту, принимающему решения, рассматривать целый спектр возможных последствий и оценивать вероятность их наступления. Этот метод демонстрирует возможности, лежащие на противоположных концах спектра (результаты игры ва-банк и принятия наиболее консервативных мер), а также вероятные последствия умеренных решений.

Впервые этим методом воспользовалась ученые, занимавшиеся разработкой атомной бомбы; его назвали в честь Монте-Карло — курорта в Монако, известного своими казино. Получив распространение в годы Второй мировой войны, метод Монте-Карло стал применяться для моделирования всевозможных физических и теоретических систем.

В рамках метода Монте-Карло анализ риска выполняется с помощью моделей возможных результатов. При создании таких моделей любой фактор, которому свойственна неопределенность, заменяется диапазоном значений — распределением вероятностей. Затем выполняются многократные расчеты результатов, причем каждый раз используется другой набор случайных значений функций вероятности. Порой для завершения моделирования бывает необходимо произвести тысячи и даже десятки тысяч перерасчетов — в зависимости от количества неопределенностей и установленных для них диапазонов. Моделирование по методу Монте-Карло позволяет получить распределения значений возможных последствий.

При использовании распределений вероятностей переменные могут иметь разные вероятности наступления разных последствий. Распределения вероятностей представляют собой гораздо более реалистичный способ описания неопределенности переменных в процессе анализа риска. Ниже перечислены наиболее распространенные распределения вероятностей.

Нормальное распределение (или «гауссова кривая»). Чтобы описать отклонение от среднего, пользователь определяет среднее или ожидаемое значение и стандартное отклонение. Значения, расположенные посредине, рядом со средним, характеризуются наиболее высокой вероятностью. Нормальное распределение симметрично и описывает множество обычных явлений — например, рост людей. К примерам переменных, которые описываются нормальными распределениями, относятся темпы инфляции и цены на энергоносители.

Логнормальное распределение. Значения имеют положительную асимметрию и в отличие от нормального распределения несимметричны. Такое распределение используется для отражения величин, которые не опускаются ниже нуля, но могут принимать неограниченные положительные значения. Примеры переменных, описываемых логнормальными распределениями, включают стоимость недвижимого имущества, цены на акции и нефтяные запасы.

Равномерное распределение. Все величины могут с равной вероятностью принимать то или иное значение, пользователь просто определяет минимум и максимум. К примерам переменных, которые могут иметь равномерное распределение, относятся производственные издержки или доходы от будущих продаж нового продукта.

Треугольное распределение. Пользователь определяет минимальное, наиболее вероятное и максимальное значения. Наибольшую вероятность имеют значения, расположенные возле точки максимальной вероятности. В число переменных, которые могут быть описаны треугольным распределением, входят продажи за минувший период в единицу времени и уровни запасов материальных оборотных средств.

PERT-распределение. Пользователь определяет минимальное, наиболее вероятное и максимальное значения — так же, как при треугольном распределении. Наибольшую вероятность имеют значения, расположенные возле точки максимальной вероятности. Однако величины в диапазоне между наиболее вероятным и предельными значениями проявляются с большей вероятностью, чем при треугольном распределении, то есть отсутствует акцент на предельных значениях. Пример использования PERT-распределения — описание продолжительности выполнения задачи в рамках модели управления проектом.

Дискретное распределение. Пользователь определяет конкретные значения из числа возможных, а также вероятность получения каждого из них. Примером может служить результат судебного процесса: 20% вероятность положительного решения, 30% вероятность отрицательного решения, 40% вероятность соглашения сторон и 10% вероятность аннулирования судебного процесса.

При моделировании по методу Монте-Карло значения выбираются случайным образом из исходных распределений вероятности. Каждая выборка значений называется итерацией; полученный из выборки результат фиксируется. В процессе моделирования такая процедура выполняется сотни или тысячи раз, а итогом становится распределение вероятностей возможных последствий. Таким образом, моделирование по методу Монте-Карло дает гораздо более полное представление о возможных событиях. Оно позволяет судить не только о том, что может произойти, но и о том, какова вероятность такого исхода.

Моделирование по методу Монте-Карло имеет ряд преимуществ по сравнению с детерминистским анализом, или анализом «по точечным оценкам»:

• Вероятностные результаты. Результаты демонстрируют не только возможные события, но и вероятность их наступления.
• Графическое представление результатов. Характер данных, получаемых при использовании метода Монте-Карло, позволяет создавать графики различных последствий, а также вероятностей их наступления. Это важно при передаче результатов другим заинтересованным лицам.
• Анализ чувствительности. За редким исключением детерминистский анализ затрудняет определение того, какая из переменных в наибольшей степени влияет на результаты. При проведении моделирования по методу Монте-Карло несложно увидеть, какие исходные данные оказывают наибольшее воздействие на конечные результаты.
• Анализ сценариев. В детерминистских моделях очень сложно моделировать различные сочетания величин для различных исходных значений, и, следовательно, оценить воздействие по-настоящему отличающихся сценариев. Применяя метод Монте-Карло, аналитики могут точно определить, какие исходные данные приводят к тем или иным значениям, и проследить наступление определенных последствий. Это очень важно для проведения дальнейшего анализа.
• Корреляция исходных данных. Метод Монте-Карло позволяет моделировать взаимозависимые отношения между исходными переменными. Для получения достоверных сведений необходимо представлять себе, в каких случаях при увеличении некоторых факторов соответствующим образом возрастают или снижаются другие.

«Делать сложно — очень просто.

А вот сделать просто — это очень сложно»

Г. С. Шпагин

Теория Решения Изобретательских Задач