Введение
Способ нахождения корней линейных и квадратичных многочленов, то есть способ решения линейных и квадратных уравнений, был известен ещё в древнем мире. Поиски формулы для точного решения общего уравнения третьей степени продолжались долгое время, пока не увенчались успехом в первой половине XVI века в трудах Сципионадель Ферро, Никколо Тарталья и ДжероламоКардано. Формулы для корней квадратных и кубических уравнений позволили сравнительно легко получить формулы для корней уравнения четвертой степени.
То, что корни общего уравнения пятой степени и выше не выражаются при помощи рациональных функций и радикалов от коэффициентов, было доказано норвежским математиком Нильсом Абелем в 1826 году.Это совсем не означает, что корни такого уравнения не могут быть найдены. Во-первых, в частных случаях, при некоторых комбинациях коэффициентов, корни уравнения всё же могут быть определены. Во-вторых, существуют формулы для корней уравнений 5-й степени и выше, использующие специальные функции — эллиптические или гипергеометрические.([1],с.192)
В случае, если все коэффициенты многочлена рациональны, то нахождение его корней приводится к нахождению корней многочлена с целыми коэффициентами. Для рациональных корней таких многочленов существуют алгоритмы нахождения перебором кандидатов с использованием схемы Горнера.
Актуальность данной курсовой работы заключается в том, что решение квадратных уравнений с помощью дискриминанта, нахождение корней уравнений с помощью схемы Горнера находит широкое применение в школе.
Объектом данной курсовой работы являются понятия «дискриминант, результант и кратные корни».
Предмет исследования – анализ теоретического материала.
Цель курсовой работы – исследование и анализ нахождения корней многочленов.
Задачи:
- раскрыть сущность понятий «дискриминант, результант и кратные корни»;
- рассмотреть свойства и способы вычисления дискриминантов и результантов;
- выявить связь между понятиями «дискриминант, результант и кратные корни многочленов»;
- рассмотреть способ нахождения кратных корней.
Глава 1. Дискриминанты и результанты многочленов
Результант.
Рассмотрим многочлены 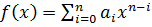 и
и 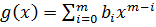 , где
, где 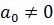 и
и 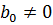 . Над алгебраически замкнутым полем многочлены
. Над алгебраически замкнутым полем многочлены 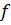 и
и 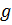 имеют общий делитель тогда и только тогда, когда они имеют общий корень. Если же поле не алгебраически замкнуто, то общий делитель может быть многочленом, не имеющим корней.([3],с.30)
имеют общий делитель тогда и только тогда, когда они имеют общий корень. Если же поле не алгебраически замкнуто, то общий делитель может быть многочленом, не имеющим корней.([3],с.30)
Наличие у 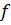 и
и 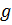 общего делителя эквивалентно тому, что существуют такие многочлены
общего делителя эквивалентно тому, что существуют такие многочлены 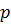 и
и 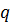 , что
, что 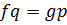 , причём
, причём 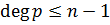 и
и 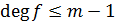 . Пусть
. Пусть 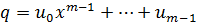 и
и 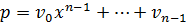 . Равенство
. Равенство 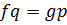 можно записать в виде системы уравнений
можно записать в виде системы уравнений
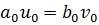 ,
,
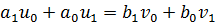 ,
,
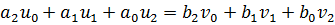 ,
,
………………………………………………..
Многочлены 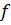 и
и 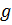 имеют общий корень тогда и только тогда, когда эта система имеет ненулевое решение
имеют общий корень тогда и только тогда, когда эта система имеет ненулевое решение 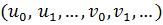 . Если, например,
. Если, например, 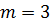 и
и 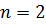 , то определитель этой системы уравнений имеют вид
, то определитель этой системы уравнений имеют вид
 .
.
Матрицу 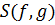 называют матрицей Сильвестра многочленов
называют матрицей Сильвестра многочленов 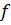 и
и 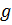 . Определитель матрицы
. Определитель матрицы 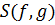 называют результантом многочленов
называют результантом многочленов 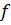 и
и 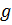 ; результант многочленов
; результант многочленов 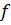 и
и 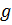 обозначают
обозначают 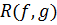 . Ясно, что
. Ясно, что 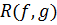 – однородный многочлен степени
– однородный многочлен степени 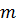 по переменным
по переменным 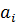 и степени
и степени 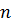 по переменным
по переменным 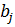 . Многочлены
. Многочлены 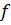 и
и 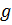 имеют общий делитель тогда и только тогда, когда определитель рассматриваемой системы равен нулю, т. е.
имеют общий делитель тогда и только тогда, когда определитель рассматриваемой системы равен нулю, т. е. 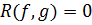 .
.
Результант имеет много разных приложений. Например, если заданы полиномиальные соотношения 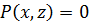 и
и 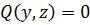 , то с помощью результанта можно получить полиномиальное соотношение
, то с помощью результанта можно получить полиномиальное соотношение 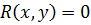 . В самом деле, рассмотрим данные полиномы
. В самом деле, рассмотрим данные полиномы 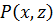 и
и 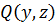 как полиномы от
как полиномы от 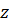 , считая
, считая 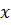 и
и 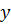 постоянными. Тогда результант
постоянными. Тогда результант 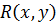 этих полиномов даст требуемое соотношение
этих полиномов даст требуемое соотношение 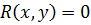 .
.
Результант позволяет также сводить решение системы алгебраических уравнений к нахождению корней многочленов. В самом деле, пусть 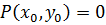 и
и 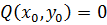 . Рассмотрим
. Рассмотрим 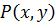 и
и 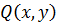 как многочлены от
как многочлены от 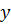 . При
. При 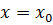 они имеют общий корень
они имеют общий корень 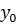 . Следовательно, их результант
. Следовательно, их результант 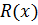 равен нулю при
равен нулю при 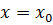 .([3],с.31)
.([3],с.31)
Теорема 1. Пусть 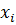 – корни многочлена
– корни многочлена 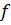 , а
, а 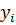 – корни многочлена
– корни многочлена 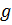 . Тогда
. Тогда
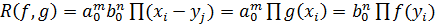 .
.
Доказательство. Так как 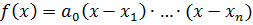 , то
, то 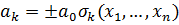 , где
, где 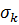 – элементарная симметрическая функция. Аналогично
– элементарная симметрическая функция. Аналогично 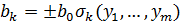 . Результант является однородным многочленом степени
. Результант является однородным многочленом степени 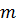 по переменным
по переменным 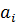 и степени
и степени 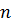 по переменным
по переменным 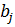 , поэтому
, поэтому
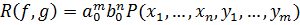 ,
,
где 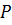 – симметрический многочлен от
– симметрический многочлен от  и
и 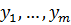 , обращающийся в нуль при
, обращающийся в нуль при 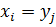 . Формула
. Формула
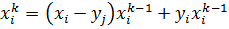
показывает, что
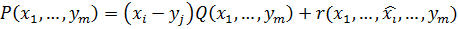 .
.
Подставив в это равенство 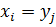 , получим, что
, получим, что 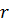 – нулевой многочлен. Аналогичные рассуждения показывают, что многочлен
– нулевой многочлен. Аналогичные рассуждения показывают, что многочлен 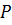 делится на
делится на 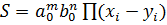 .
.
Так как 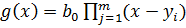 , то
, то 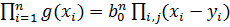 , а значит,
, а значит,
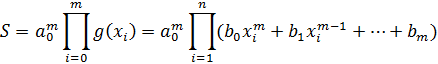
-однородный многочлен степени 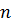 по переменным
по переменным 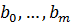 . Для переменных
. Для переменных  рассуждения аналогичны. Ясно также, что симметрический многочлен
рассуждения аналогичны. Ясно также, что симметрический многочлен 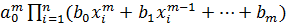 является многочленом от
является многочленом от 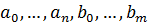 . Следовательно,
. Следовательно, 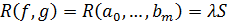 , где
, где 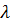 – некоторое число. С другой стороны, коэффициент при
– некоторое число. С другой стороны, коэффициент при 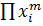 у многочленов
у многочленов 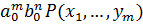 и
и 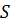 равен
равен  , поэтому
, поэтому 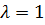 .
. 
Следствие 1. 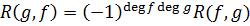 .([3],с.32)
.([3],с.32)
Следствие 2. Если 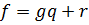 , то
, то
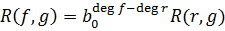 ,
,
где 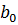 - старший коэффициент многочлена
- старший коэффициент многочлена 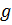 .
.
Доказательство. Пусть 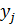 - корни многочлена
- корни многочлена 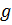 . Тогда
. Тогда 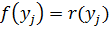 .Остаётся воспользоваться тем, что
.Остаётся воспользоваться тем, что 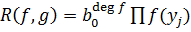 и
и 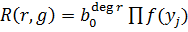 .
. 
Следствие 3. 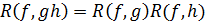 .
.
Доказательство. Пусть 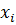 - корни многочлена
- корни многочлена 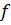 , а
, а  - его старший коэффициент. Тогда
- его старший коэффициент. Тогда
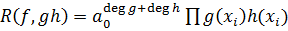 ,
,
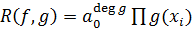 ,
,
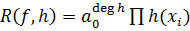 .
. 
Теорема 2. Пусть 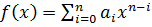 и
и 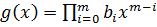 . Тогда существуют многочлены
. Тогда существуют многочлены 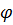 и
и 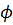 с целыми коэффициентами от переменных
с целыми коэффициентами от переменных 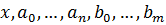 , для которых выполняется равенство
, для которых выполняется равенство
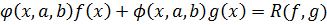 .
.
Доказательство. Пусть 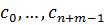 - столбцы матрицы Сильвестра
- столбцы матрицы Сильвестра 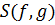 и
и 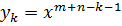 . Тогда
. Тогда 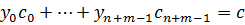 , где
, где 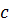 – столбец (
– столбец ( . Рассмотрим это равенство как систему линейных уравнений относительно
. Рассмотрим это равенство как систему линейных уравнений относительно 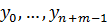 и воспользуемся правилом Крамера, чтобы найти
и воспользуемся правилом Крамера, чтобы найти 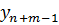 . В результате получим
. В результате получим
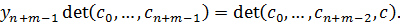 (1)
(1)
Остаётся заметить, что 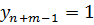 ,
, 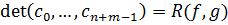 , а определитель, стоящий в правой части равенства (1), можно представить в требуемом виде.
, а определитель, стоящий в правой части равенства (1), можно представить в требуемом виде.  ([3],с.33)
([3],с.33)
Дискриминант.
Пусть  - корни многочлена
- корни многочлена 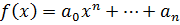 , причём
, причём 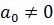 . Величину
. Величину 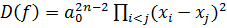 называют дискриминантом многочлена
называют дискриминантом многочлена 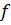 .
.
Теорема 1. 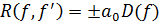 .
.
Доказательство. По теореме 1 пункта 1.1 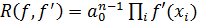 , где
, где 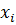 – корни многочлена
– корни многочлена 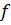 . Легко проверить, что
. Легко проверить, что 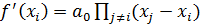 . Поэтому
. Поэтому
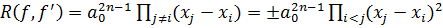 .
. 
Замечание. Несложно показать, что
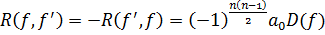 .
.
Следствие. Дискриминант является многочленом с целыми коэффициентами от коэффициентов многочлена 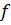 .
.
Теорема 2. Пусть 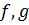 и
и 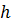 - многочлены со старшим коэффициентом 1. Тогда
- многочлены со старшим коэффициентом 1. Тогда
 ,
,
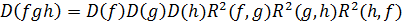 .
.
Доказательство. Пусть  - корни многочлена
- корни многочлена 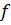 , а
, а 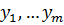 - корни многочлена
- корни многочлена 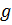 . Тогда
. Тогда
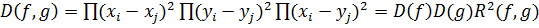 .
.
Вторая формула доказывается аналогично. 
Теорема 3. Пусть 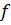 – вещественный многочлен степени
– вещественный многочлен степени 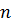 , не имеющий вещественных корней. Тогда
, не имеющий вещественных корней. Тогда 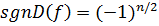 .([3],с.34)
.([3],с.34)
Доказательство. Воспользовавшись разложением
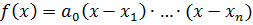 ,
,
Легко проверить, что
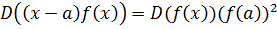 .
.
Пусть 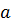 и
и 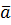 - пара сопряжённых корней многочлена
- пара сопряжённых корней многочлена 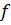 , т.е.
, т.е.
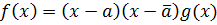 .
.
Тогда
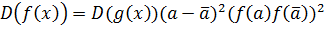 .
.
Ясно, что 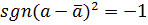 и
и 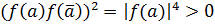 . Поэтому
. Поэтому 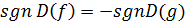 . Требуемое утверждение теперь легко доказывается индукцией по
. Требуемое утверждение теперь легко доказывается индукцией по 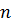 .
. 
Теорема 4. Пусть 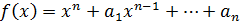 – многочлен с целыми коэффициентами. Тогда его дискриминант
– многочлен с целыми коэффициентами. Тогда его дискриминант 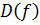 имеет вид
имеет вид 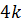 или
или 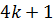 , где
, где 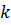 – целое число.
– целое число.
Доказательство. Пусть  – корни многочлена
– корни многочлена 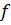 . Тогда
. Тогда 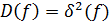 , где
, где  . Рассмотрим вспомогательную величину
. Рассмотрим вспомогательную величину  . Ясно, что
. Ясно, что 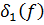 – симметрическая функция от корней многочлена
– симметрическая функция от корней многочлена 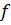 , поэтому
, поэтому 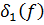 – целое число. Кроме того,
– целое число. Кроме того,
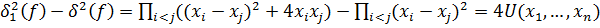 ,
,
где 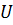 – симметрический многочлен от
– симметрический многочлен от  с целыми коэффициентами. Поэтому
с целыми коэффициентами. Поэтому 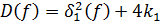 , где
, где 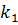 – целое число. Ясно также, что
– целое число. Ясно также, что 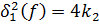 или
или 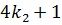 .
.  ([3],с.35)
([3],с.35)
Вычисление некоторых результантов и дискриминантов.
Пример 1. 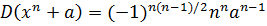 .
.
Доказательство. Воспользуемся тем, что
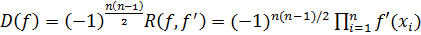 ,
,
где  – корни многочлена
– корни многочлена 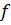 . В нашем случае
. В нашем случае 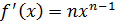 и
и 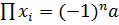 , а значит,
, а значит, 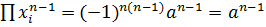 .
. 
Пример 2. 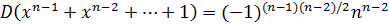 .
.
Доказательство. Рассматриваемый многочлен 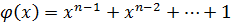 удовлетворяет соотношению
удовлетворяет соотношению 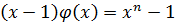 . Поэтому
. Поэтому
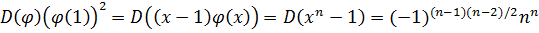 .
.
Остаётся заметить, что 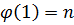 .
. 
Пример 3. Пусть 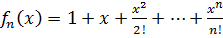 . Тогда
. Тогда
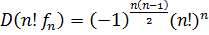 .
.
Доказательство. Коэффициент при старшем члене многочлена 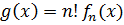 равен 1, поэтому
равен 1, поэтому
 ,
,
где 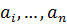 – корни многочлена
– корни многочлена  .
.
Ясно, что 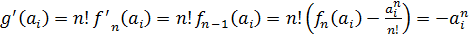 .
.
Поэтому
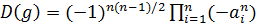 .
.
Остаётся заметить, что 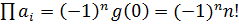 .
. 
Пример 4. Пусть 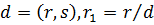 и
и 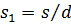 . Тогда
. Тогда
 .([3],с.36)
.([3],с.36)
Доказательство. Соотношение 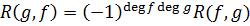 показывает, что если требуемое утверждение верно для пары
показывает, что если требуемое утверждение верно для пары 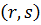 , то оно верно и для пары
, то оно верно и для пары 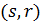 .В самом деле,
.В самом деле, 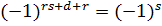 . Таким образом, можно считать, что
. Таким образом, можно считать, что 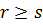 .
.
При 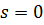 утверждение очевидно. Если
утверждение очевидно. Если 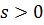 , то, поделив
, то, поделив 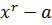 на
на 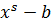 , получим остаток
, получим остаток 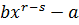 . Поэтому
. Поэтому
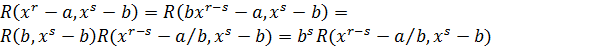 .
.
Легко видеть, что если 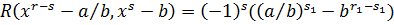 , то
, то 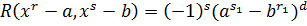 . Остаётся применить индукцию по
. Остаётся применить индукцию по 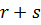 .
.
Пример 5. Пусть 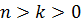 ,
, 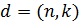 ,
, 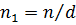 и
и 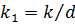 . Тогда
. Тогда 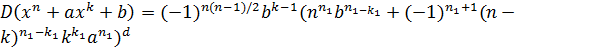 .
.
Доказательство. Из формулы 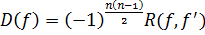
получаем
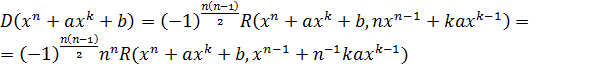 .
.
Воспользовавшись тем, что
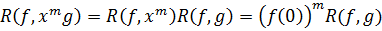 ,
,
получим
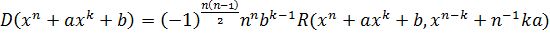 .
.
Остаток от деления многочлена 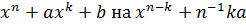 равен
равен  , поэтому
, поэтому
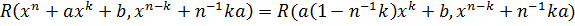 .
.
Результант пары двучленов вычислен в предыдущем примере.  ([3],с.37)
([3],с.37)