Понятие корня и кратного корня.
Элемент 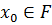 называется корнем кратности
называется корнем кратности 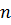 многочлена
многочлена  , если
, если 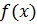 делится без остатка на
делится без остатка на  , но не делится на
, но не делится на 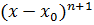 . Корень кратности 1 называется простым.([2],с.152)
. Корень кратности 1 называется простым.([2],с.152)
Число корней многочлена степени 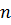 не превышает
не превышает 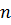 даже в том случае, если кратные корни учитывать кратное количество раз.
даже в том случае, если кратные корни учитывать кратное количество раз.
Всякий многочлен 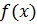 с комплексными коэффициентамиимеетпо крайней мере один, вообще говоря, комплексный, корень (основная теорема алгебры).
с комплексными коэффициентамиимеетпо крайней мере один, вообще говоря, комплексный, корень (основная теорема алгебры).
Число комплексных корней многочлена с комплексными коэффициентами степени 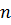 , учитывая кратные корни кратное количество раз, равно
, учитывая кратные корни кратное количество раз, равно 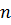 . При этом все чисто комплексные корни (если они есть) многочлена с вещественными коэффициентами можно разбить на пары сопряжённых одинаковой кратности, таким образом, многочлен чётной степени с вещественными коэффициентами может иметь только чётное число вещественных корней, а нечётной — только нечётное.
. При этом все чисто комплексные корни (если они есть) многочлена с вещественными коэффициентами можно разбить на пары сопряжённых одинаковой кратности, таким образом, многочлен чётной степени с вещественными коэффициентами может иметь только чётное число вещественных корней, а нечётной — только нечётное.
Корни многочлена связаны с его коэффициентами формулами Виета.[4]
Критерий кратности корней.
Теорема. Элемент 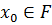 является корнем многочлена
является корнем многочлена 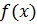 кратности
кратности 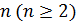 тогда и только тогда, когда
тогда и только тогда, когда  и он является корнем кратности
и он является корнем кратности  у производной многочлена
у производной многочлена 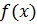 .
.
Доказательство.
Необходимость. Пусть 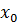 - корень кратности
- корень кратности 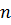 многочлена
многочлена 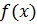 , тогда по определению
, тогда по определению  , где
, где 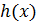 не делится на
не делится на 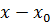 . Применим теорему (для любых многочленов
. Применим теорему (для любых многочленов 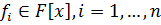 , и любого натурального
, и любого натурального 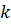 справедливо равенство
справедливо равенство 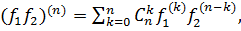 где
где 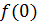 обозначает
обозначает 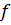 ).
).
Отсюда имеем, что

Следовательно,  делится на
делится на 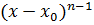 , но не делится на
, но не делится на  , так как
, так как 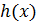 не делится на
не делится на 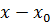 .
.
Достаточность. Пусть  и
и  делится
делится 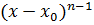 . Докажем, что
. Докажем, что 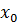 – корень кратности
– корень кратности 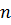 многочлена
многочлена 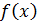 . Предположим, что
. Предположим, что 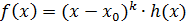 , где
, где 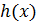 не делится на
не делится на 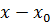 . Тогда
. Тогда

многочлен 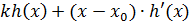 не делится на
не делится на 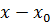 и, следовательно,
и, следовательно, 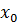 является корнем кратности
является корнем кратности  производной
производной  , откуда
, откуда 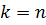 .
.  ([2],с.152)
([2],с.152)
Любой многочлен 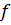 может быть единственным образом разложен по степеням
может быть единственным образом разложен по степеням 
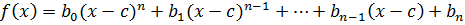
Это легко доказывается индукцией по степени многочлена. Действительно, разделим 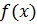 на
на  с остатком. Получим
с остатком. Получим
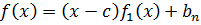 ,
,
где  – остаток,
– остаток,  – многочлен степени
– многочлен степени  . В силу индуктивного предположения
. В силу индуктивного предположения
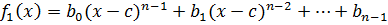 ,
,
откуда 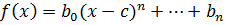 .
.
Опишем алгоритм для вычисления коэффициентов 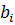 . Свободный член
. Свободный член  разложения есть остаток от деления
разложения есть остаток от деления 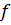 на
на  ,
, 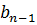 есть остаток при делении неполного частного
есть остаток при делении неполного частного  на
на  , и вычисление последующих коэффициентов требует вычисления неполного частного
, и вычисление последующих коэффициентов требует вычисления неполного частного 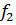 при делении
при делении  на
на  . Далее,
. Далее, 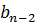 находится как остаток при делении
находится как остаток при делении 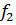 на
на  и т.д.
и т.д.
Красивые формулы для коэффициентов 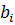 указывает следующая теорема.
указывает следующая теорема.
Теорема(Тейлор). Любой многочлен 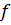 степени
степени 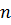 можно представить в виде
можно представить в виде
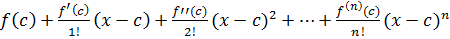 .
.
Доказательство. Пусть
 .
.
Продифференцируем 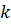 раз обе части этого равенства. Используя правила дифференцирования, получаем, что
раз обе части этого равенства. Используя правила дифференцирования, получаем, что 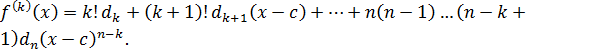
Полагая 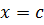 , имеем
, имеем  .
.  ([2],с.153)
([2],с.153)
Схема Горнера.
Деление произвольного многочлена на двучлен может быть выполнено существенно проще, чем деление на произвольный многочлен.
Действительно, если нужно разделить многочлен

на двучлен  , где
, где  , т.е. найти такие
, т.е. найти такие  и
и 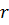 , что
, что 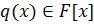 ,
,  , и
, и 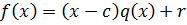 , естественно искать
, естественно искать 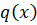 в форме
в форме 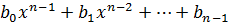 . Тогда получим равенство
. Тогда получим равенство
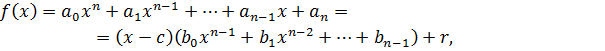
равносильное цепочке равенств
 ,
,
 ,
,
 ,
,
……………………
 ,
,
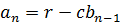 ,
,
откуда последовательно определяются коэффициенты  и остаток
и остаток 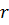 :
:
 ,
,
 ,
,
 ,
,
……………………
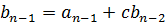 ,
,
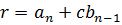 .
.
Заметим, что остаток 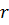 равен значению
равен значению  многочлена
многочлена 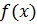 при
при 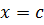 .
.
Действительно, переходя в равенстве 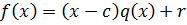 к значениям при
к значениям при 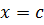 , получим
, получим  , откуда
, откуда 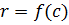 .
.
Указанный способ вычисления коэффициентов частного 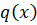 и остатка
и остатка 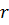 носит название схемы Горнера.([2],с.154-155)
носит название схемы Горнера.([2],с.154-155)
Пример 1. Разложить многочлен 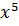 по степеням
по степеням  .
.
Применим схему Горнера.
| 32 | |||||
| 80 | |||||
| 80 | |||||
| 40 | |||||
| 10 | |||||
| 1 |
Остатки подчёркнуты.
Таким образом,  .
.
Для приближённого вычисления корней многочлена бывает нужно найти одновременно  и
и  . Выполнить это можно при помощи схемы Горнера, вычислив два коэффициента разложения
. Выполнить это можно при помощи схемы Горнера, вычислив два коэффициента разложения 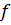 по степеням
по степеням  .
.
Пример 2.
Для многочлена 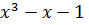 вычислить
вычислить 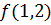 и
и  .
.
Применим схему Горнера.
| -1 | -1 | ||
| 1,2 | 0,44 | -0,472 | |
| 2,4 | 3,32 |
Итак,  и
и 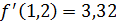 .
.
Список использованной литературы
1. «Теорема Абеля в задачах и решениях» – М.:МЦНМО,2001г.
2. Гашков С.Б. «Современная элементарная алгебра в задачах и упражнениях»– МЦНМО,2006.
3. Прасолов В.В. «Многочлены» – МЦНМО,2003. Издание третье, исправленное.
4. ru.wikipedia.org(12.12.13г.)