Зададим на отрезке 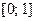 конечное множество точек (узлов)
конечное множество точек (узлов)  . Множество
. Множество  − сетка, h − шаг сетки. Обозначим
− сетка, h − шаг сетки. Обозначим  подмножество множества
подмножество множества  , полученное из множества
, полученное из множества  отбрасыванием крайних (граничных) узлов
отбрасыванием крайних (граничных) узлов  . Множество узлов
. Множество узлов  тоже называется сеткой. Пусть также
тоже называется сеткой. Пусть также  − сетка, состоящая из двух граничных узлов. Таким образом,
− сетка, состоящая из двух граничных узлов. Таким образом,  (сетка
(сетка  является объединением сеток
является объединением сеток  и
и  ). На рис. 1.6 изображены сетки: в кружки помещены узлы, принадлежащие сетке
). На рис. 1.6 изображены сетки: в кружки помещены узлы, принадлежащие сетке  , а в квадратиках расположены граничные узлы, образующие сетку
, а в квадратиках расположены граничные узлы, образующие сетку  .
.

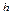
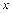

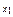
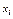


Рис. 1.6
Обозначим 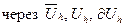 множества всех сеточных функций, определенных соответственно
множества всех сеточных функций, определенных соответственно  . Множество
. Множество  (а также
(а также 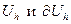 ) является линейным пространством, в котором операции умножения функции на число и сложения функций выполняются по обычным правилам. В линейных пространствах
) является линейным пространством, в котором операции умножения функции на число и сложения функций выполняются по обычным правилам. В линейных пространствах  сеточных функций зададим соответственно нормы
сеточных функций зададим соответственно нормы
 .
.
Разностные операторы
Оператор 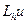 называется разностным, если он каждой сеточной функции
называется разностным, если он каждой сеточной функции  ставит в соответствие некоторую сеточную функцию, принадлежащую
ставит в соответствие некоторую сеточную функцию, принадлежащую  (или
(или  ).
).
Примеры разностных операторов:
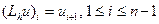 ;
;
 ;
;
 ;
;

Индекс i в левой части указывает номер узла, в котором оператор принимает данное справа значение. Какова бы ни была сеточная функция  , в примерах 1, 3 имеем
, в примерах 1, 3 имеем 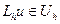 , а в примерах 2, 4 имеем
, а в примерах 2, 4 имеем 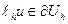 .
.
Для удобства определение разностного оператора дано в широком смысле, не требуя явной его зависимости от разностей первого или более высоких порядков, а только от значений сеточной функции, имея также в виду, что сами значения сеточной функции можно формально считать разностями нулевого порядка.
Заменяя, дифференциальный оператор L некоторым разностным оператором  , мы допускаем ошибку – погрешность аппроксимации, от величины которой будет зависеть точность решения разностной задачи.
, мы допускаем ошибку – погрешность аппроксимации, от величины которой будет зависеть точность решения разностной задачи.
Выясним величину погрешности аппроксимации дифференциального оператора разностным оператором для формул I−III, VI−X, используя разложение в ряд Тейлора решения дифференциальной задачи
 .
.
Вычислим  для каждой из указанных формул:
для каждой из указанных формул:

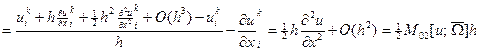 ;
;

 ;
;


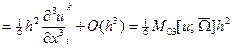 ;
;
 ;
;

 ;
;

 ;
;

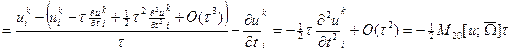 ;
;
 ;
;
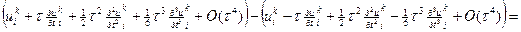
 ;
;
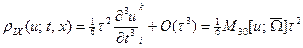 .
.
Итак, для остаточного члена справедливы оценки:
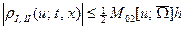 или
или  ;
;
 или
или  ;
;
 или
или  ;
;
 или
или  ; или
; или  .
.
Порядок величины функции.
Следующие определения дают возможность сравнивать две функции.
Для сравнения порядка величин двух функций f и g употребляются символы o и O.
Если для двух функций f и g  , то пишут:
, то пишут:  .
.
Пример 3. 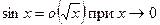 .
.
Если существует такое 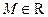 , что для двух функций f и g
, что для двух функций f и g  , то пишут
, то пишут 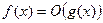 .
.
Пример 4.  .
.
Исследование сходимости разностной схемы проводится в два этапа:
1) устанавливают аппроксимацию задача (1.1) разностной схемы (1.2);
2) проверяют устойчивость разностной схемы.
 Говорят, что разностная схема (1.2) аппроксимирует задачу (1.1), если
Говорят, что разностная схема (1.2) аппроксимирует задачу (1.1), если
 , (1.7)
, (1.7)
величину 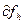 называют погрешностью аппроксимации.
называют погрешностью аппроксимации.
 Если
Если
 , (1.8)
, (1.8)
то говорят, что разностная схема (1.2) аппроксимирует задачу на решении  с порядком s относительно h.
с порядком s относительно h.
Перейдем к рассмотрению конкретных примеров. Пока будем рассматривать различные схемы для решения эволюционных задач.