Рассмотрим уравнение теплопроводности
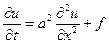, (2.1)
где 
– постоянная величина и 
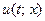ищется в полуполосе 
. Правую часть уравнения – функцию f – будем считать заданной и непрерывной в той же полуполосе.
Для уравнения (2.1) могут быть поставлены различные краевые условия, но мы ограничимся рассмотрением первой краевой задачи. Будем предполагать, следовательно, что уравнение (2.1) сопровождается начальным условием
(2.2)
и граничными условиями
(2.3)
Как всегда, предполагаем существование и единственность решения 
задачи (2.1) –(2.3). При этом функция 
считается решением задачи (2.1) – (2.3), если она непрерывна в полуполосе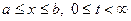 
вместе с производными первого порядка по t и до второго порядка включительно по x. Кроме того, она удовлетворяет уравнению (2.1) во всех точках полуполосы, начальным условиям (2.2) во всех точках отрезка 
, граничным условиям (2.3) во всех точках лучей 
, и 
соответственно. Таким образом, предположение о существовании решения накладывает дополнительные требования на гладкость функций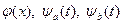 
. Потребуем соблюдения условий согласования
.
Эти условия являются необходимыми для того, чтобы функция была непрерывна вплоть до границы.
Обычно ограничиваются рассмотрением конечного промежутка времени, т.е. вместо полуполосы 
ищут решение в прямоугольнике 
.
1. В области 
введем равномерную прямоугольную сетку 
с шагом 
по оси x и с шагом τ по оси t. Построим сетку 
, где 
. Положим 
(тогда 
), 
.
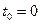Рис. 2.1
Покажем, как несущественные с первого взгляда различия в аппроксимации дифференциального уравнения приводят к разностным схемам с различными свойствами. С этой целью приведем четыре разностные схемы для численного интегрирования задачи (2.1) – (2.3), причем три первые их них разнятся лишь аппроксимацией производной по времени.
Вариант 1: явная разностная схема
2. Применяя формулу (VII) для аппроксимации 
разностными отношениями и формулу (VI) для аппроксимации 
, напишем разностный аналог уравнения (2.1).
3. 
. (2.4)
Для остаточного члена 
справедлива оценка
.
Вводя обозначения 
, напишем соотношение (2.4) для расчетной точки 
:
. (2.5)
Отбрасывая остаточный член, получаем искомое разностное уравнение:
. (2.6)
Рассматриваемому варианту 1 отвечает следующий шаблон (рис. 2.2), в котором кружком с крестиком обозначена расчетная точка.
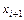
Рис. 2.2
Шаблон варианта 1 является четырехточечным двухслойным.
4. Пусть m есть целая часть отношения 
. Из начальных и граничных условий находим
, (2.7)
. (2.8)
В силу условий согласования равенства 
и 
, а также 
и 
совместны.
5. Учитывая (2.7), (2.8), разностная схема (2.6) имеет 
неизвестных значений
.
Подсчитаем количество имеющихся в нашем распоряжении уравнений для варианта 1. При этом следует позаботиться, чтобы в уравнения не входили новые неизвестные, т.е. чтобы все узлы сетки, принадлежащие шаблону, не выходили за пределы .
Уравнения (2.6) пишем для значений 
, так что число уравнений оказывается равным числу неизвестных.
Рассмотрим вопрос о том, как решать систему линейных алгебраических уравнений (2.6). Пусть 
. Введем сечения 
.
Оказалось удобнее не включать в сечение 
крайние значения 
и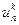 
. Таким образом, задание равносильно заданию сечений 
и крайних значений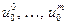 
, 
. В частности, при решении системы сеточных уравнений заданы равенствами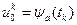 
, а 
– равенствами 
.
Как и следовало ожидать, определение сеточной функции из системы уравнений (2.6) – (2.8) сводится к последовательному определению 
.
В двухслойном шаблоне для варианта 1 в верхнем слое расположена всего лишь одна точка. Следовательно, если мы уже знаем сечение , то из уравнений (2.6), мы сможем найти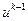 
. Достаточно для этого преобразовать уравнение (2.6) к виду
, (2.9)
где
.
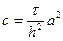При счете по формуле (2.9) для значени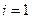й 
и 
будут использованы значения 
и , полученные в (2.8) из граничных условий. Поскольку нулевое сечение 
известно, счет по формулам (2.9) позволяет определить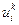 
для всех нужных пар 
.
Таким образом, использование варианта 1 полностью освобождает нас от необходимости решать системы линейных уравнений, сводя дело к счету по рекуррентной формуле (2.9). В связи с тем, что в уравнениях (2.9) составляющие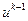 
явно выражаются через значения составляющих , схему варианта 1 называют явной.
Вариант 2: неявная разностная схема
2. Применяя формулу (VIII) для аппроксимации 
разностными отношениями и формулу (VI) для аппроксимации , напишем разностный аналог уравнения (2.1).
3. 
(2.10)
Для остаточного члена справедлива оценка
.
Вводя обозначения 
, напишем соотношение (2.10) для расчетной точки 
:
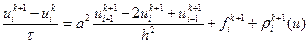. (2.11)
Отбрасывая остаточный член, получаем искомое разностное уравнение:
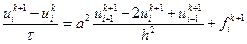. (2.12)
Рассматриваемому варианту 2 отвечает следующий шаблон (рис. 2.3), в котором кружком с крестиком обозначена расчетная точка.
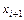
Рис. 2.3
Шаблон варианта 2 является четырехточечным двухслойным.
4. Пусть m есть целая часть отношения . Из начальных и граничных условий находим
, (2.7)
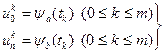. (2.8)
В силу условий согласования равенства 
и , а также 
и совместны.
5. Учитывая (2.7), (2.8), разностная схема (2.6) имеет неизвестных значений
.
Подсчитаем количество имеющихся в нашем распоряжении уравнений для варианта 2. При этом следует позаботиться, чтобы в уравнения не входили новые неизвестные, т.е. чтобы все узлы сетки, принадлежащие шаблону, не выходили за пределы .
Уравнения (2.12) пишем для значений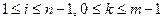 
, так что число уравнений оказывается равным числу неизвестных.
Рассмотрим вопрос о том, как решать систему линейных алгебраических уравнений (2.6). Пусть . Введем сечения 
.
Оказалось удобнее не включать в сечение 
крайние значения и 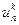. Таким образом, задание равносильно заданию сечений и крайних значений 
, 
. В частности, при решении системы сеточных уравнений заданы равенствами 
, а – равенствами 
.
Как и следовало ожидать, определение сеточной функции из системы уравнений (2.12), (2.7), (2.8) сводится к последовательному определению .
Уравнения (2.12) при первом взгляде мало отличаются от уравнений (2.6). Однако шаблон варианта 2 весьма существенно разнится от шаблона варианта 1. В шаблоне варианта 2 в верхнем слое расположены три точки, а не одна, как в шаблоне варианта 1. В связи с этим из формул (2.12) не удается извлечь явного выражения для составляющих 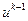через составляющие . Приходится действовать иначе. Преобразуем уравнения (2.12) к виду
. (2.13)
С учетом того, что значения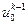 
и 
, известны из (2.8), мы имеем дело с системой 
линейных уравнений с неизвестными 
. Для того, чтобы от k -го слоя продвинуться к 
слою, следует решить эту систему. В связи с этим схему варианта 2 называют неявной. Зная из (2.7) значения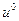 
и на каждом слое и 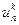, мы последовательно находим 
. Замечаем, что система (2.13) имеет трехдиагональную матрицу, которая связывает неизвестные значения сеточных функций в трех соседних узлах сетки. При этом число арифметических действий, нужны для решения системы (2.13), примерно равно 
.
Метод прогонки
Перепишем систему (2.8), (2.13) следующим образом (для одного временного слоя, при этом опуская верхний индекс):
(2.14)
где
,
.
Оказывается, что для систем уравнений вида (2.14) существует простой и удобный метод решения, который во всех случаях к тому же еще слабо чувствителен к вычислительным погрешностям. Он представляет собой один из вариантов хорошо известного метода Гаусса исключения неизвестных и носит название метода прогонки. Опишем этот метод.
Специфика системы (2.14) заключается в том, что каждое i -е уравнение содержит только три неизвестных: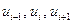 
. Это дает возможность провести последовательное исключение 
следующим простым способом. Значение 
задано. Уравнение 
можно, положив
, (2.15)
переписать так
. (2.16)
Из уравнения 
, отвечающего в системе (2.14) номеру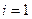 
, исключим 
с помощью равенства (2.16)
.
Если только 
, что мы будем сейчас предполагать, то
.
После введения обозначений
(2.17)
неизвестное 
выражается через неизвестное 
с помощью соотношения
. (2.18)
Соотношением (2.18) можно воспользоваться, чтобы исключить 
из уравнения
.
Это уравнение отвечает номеру 
. Результат исключения запишем в явном относительно 
виде
. (2.19)
Описанный процесс исключения можно продолжить для номеров 
.
Пусть мы уже имеем соотношение
. (2.20)
Исключив с его помощью 
из уравнения
,
получим
.
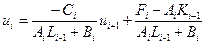Отсюда видно, что коэффициенты получаемых в процессе исключения соотношений
(2.21)
вычисляются по рекуррентным формулам
. (2.22)
Получив соотношение
(2.23)
и учитывая, что 
, можно вычислить 
. После этого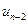 
определится из равенства
,
из равенства
.
И так далее, пока не будут последовательно определены все 
.
Повторим кратко, в чем состоит описанный сейчас вычислительный процесс.
1) принимаем ;
2) по рекуррентным формулам
. (2.22)
последовательно вычисляем 
;
3) зная 
, по формуле
(2.21)
вычисляем 
.
Первые два шага называют прямой прогонкой, последний шаг – обратной прогонкой. Они выполнены при условии, что 
.
Коэффициенты 
называют прогоночными коэффициентами. Так как значения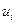 
находятся здесь последовательно от номера 
к номеру i, то формулы (2.15), (2.22), (2.21) называют иногда формулами правой прогонки.
Элементарный подсчет арифметических действий в формулах (2.15), (2.22), (2.21) показывает, что реализация метода прогонки по этим формулам требует выполнения 
умножений, 
делений и сложений и вычитаний. Если не делать различия между арифметическими операциями, то общее их число для метода прогонки есть 
. Из этого числа 
операции затрачиваются на вычисление 
и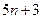 
операции на вычисление 
и .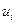
На решение произвольной линейной системы n уравнений с n неизвестными методом исключения приходится обычно затрачивать арифметические действия в количестве порядка 
. Такого сокращения числа арифметических действий при решении системы (2.14) методом прогонки удалось достигнуть, удачно используя специфику этой системы.
Можно показать, что одно из условий хорошей обусловленности для системы (2.14) при решении ее методом прогонки есть
.
При этом условии выражения 
, на которые приходиться делить, не обращаются в нуль, а погрешности, допускаемые в процессе вычислений, не накапливаются и не приводят к возрастающим с ростом n ошибкам в вычисляемых значениях решения.
Эти два замечательных свойства прогонки – малое число арифметических действий для ее реализации и слабая чувствительность к вычислительным погрешностям – делают прогонку очень удобным вычислительным алгоритмам.