Рассмотрим дискретный сигнал, представленный упорядоченным набором чисел { x (k)}, где k – целое число в диапазоне 0– N –1. Пусть T д – период дискретизации, ωд=2π/ T д – круговая частота дискретизации. Для представления дискретного сигнала в аналитическом виде обычно используют формулу
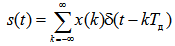, (1)
где δ(t) – дельта-функция.
Рассчитаем спектр сигнала s (t)
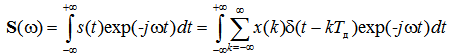(2)
Так как преобразование Фурье является линейным оператором и x (k) является константой (что означает, что x (k) можно вынести за знак интеграла) получаем
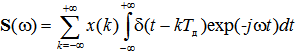(3)
Функция спектральной плотности дельта-функции равна единице на всей области частот. Так как дельта-функция задержана на kT д ее спектр получает дополнительный множитель exp(– jkT дω) и выражение (3) можно преобразовать следующим образом
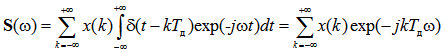(4)
Формула (4) показывает, что спектр дискретного сигнала является периодической функцией с круговой частотой равной периоду дискретизации T д или периодом 2π/ T д, т.е. S (ω) = S (ω ± n ωд), где n – целое число. Формула (4) позволяет вычислить функцию спектральной плотности по известным отсчетам сигнала.
Сейчас мы вывели очень важное соотношение цифровой обработки сигналов. Стоит запомнить, что спектр периодического сигнала является дискретным (или решетчатым), а спектр дискретного(решетчатого) сигнала является периодическим.
Теперь выполним несколько иную задачу. Пусть цифровой сигнал x (k) является результатом дискретизации аналогового сигнала s (t), тогда выполняется соотношение
x (k) = s (kT д)
Тогда дискретный сигнал можно представить в аналитическом виде следующим образом
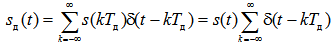(5)
Выведем соотношение связывающее спектры аналогового сигнала S (ω) и результата его дискретизации S д(ω)
Заметим, что функция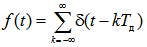 
является периодическим сигналом (повторяющимися с периодом T д дельта-функциями). Так как в интервал (– T д/2, T д/2) попадает только одна дельта-функция, функцию f (t) можно разложить в ряд Фурье следующим образом. Вычислим коэффициенты комплексного ряда Фурье
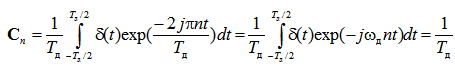(6)
Таким образом функция f (t) может быть представлена рядом Фурье
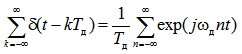(7)
Подставим (7) в (5) и получим
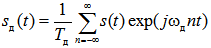(8)
Умножение функции на exp(j ωд nt) соответствует сдвигу функции спектральной плотности на ωд n. Тогда спектр аналогового сигнала связан со спектром дискретизированного представления выражением
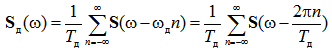(9)
По формуле (9) видно, что спектр дискретного сигнала представляет собой сумму сдвинутых копий аналогового сигнала. Расстояние между соседними копиями равно частоте дискретизации ωд = 2π/ T д. Данное обстоятельство продемонстрировано на рисунке 1, на котором представлен спектр дискретного сигнала.
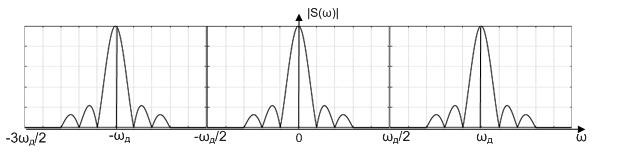
Рисунок 1 – Спектр дискретного сигнала
Аналоговый сигнал может быть восстановлен по дискретному представлению путем низкочастотной фильтрации с частотой среза ωд/2. Частота ωд/2 называется частотой Найквиста, о которой мы говорили при рассмотрении теоремы отсчетов. Очевидно, что аналоговый сигнал может быть корректно восстановлен только в том случае, если он не содержит частот выше частоты Найквиста (то есть половины частоты дискретизации). В противном случае копии спектров будут перекрываться и мы получим алиазинговый или стробоскопический эффект (то есть возникновение ложных частот). Продемонстрируем возникновение данного эффекта на примере оцифровки гармонического сигнала с частотой ω s, находящейся на интервале (ωд/2, ωд). Спектр аналогового гармонического сигнала был рассмотрен нами в предыдущих статьях и представляет собой пару дельта функций (рисунок 2)
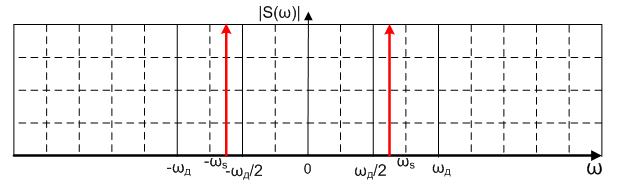
Рисунок 2 – Спектр аналогового гармонического сигнала
Спектр дискретизированного сигнала представляет собой сдвинутые на ωд копии спектра аналогового сигнала (рисунок 3)
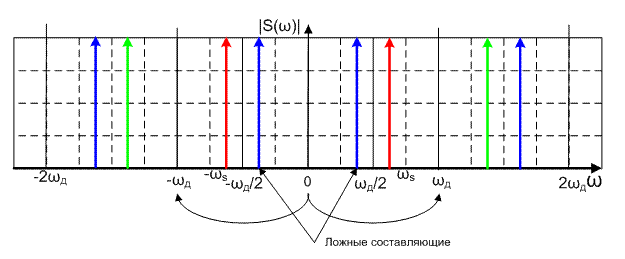
Рисунок 3 – Спектр дискретного гармонического сигнала
После пропускания цифрового сигнала через ФНЧ с частотой среза ωд/2, получим аналоговый сигнал со спектром представленном на рисунке 4.
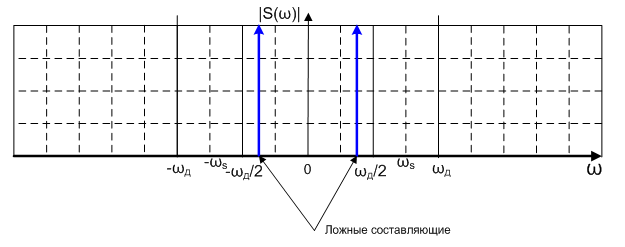
Рисунок 4 – Ложные частоты в спектре восстановленного аналогового сигнала
Как мы видим, мы получили результат отличный от спектра исходного сигнала. При этом мы имеем две ложные гармоники с частотами ±(ωд – ω s).
В случае произвольного сигнала имеющего частотные составляющие выше частоты Найквиста копии спектров будут перекрываться, следствием чего будет появление ложных частот наглядно продемонстрированное нами выше. Поэтому перед оцифровкой аналоговый сигнал пропускают через ФНЧ с частотой среза равной частоте Найквиста. Стоит отметить, что перед построением цифровой системы проводят тщательный анализ частотных свойств сигнала, так как если неправильно выбрать частоту дискретизации (слишком занизить), то можно потерять часть полезного высокочастотного сигнала. При этом сигнал будет потерян в случае использования ФНЧ перед аналогово-цифровым преобразованием или искажен (перенесен в низкочастотную область) при возникновении алиазингового эффекта. Поэтому частоту дискретизации ωд необходимо выбрать такой, чтобы аналоговый сигнал, оцифровываемый проектируемой системой, не нес полезной информации на частотах выше частоты Найквиста ωд/2. Стоит отметить, что существуют исключения из правил и некоторые системы специально строятся с возможностью обработки сигналов с эффектом алиазинга. Как правило, такие системы предназначены для обработки периодических (гармонических) сигналов.
Выше мы рассмотрели случай, когда в качестве дискретизирующих импульсов выступает дельта функция. На практике обычно цифровой сигнал на выходе цифро-аналогового преобразователя представляет собой набор, сменяющихся в дискретные моменты времени, прямоугольных импульсов с разными амплитудами (рисунок 5).
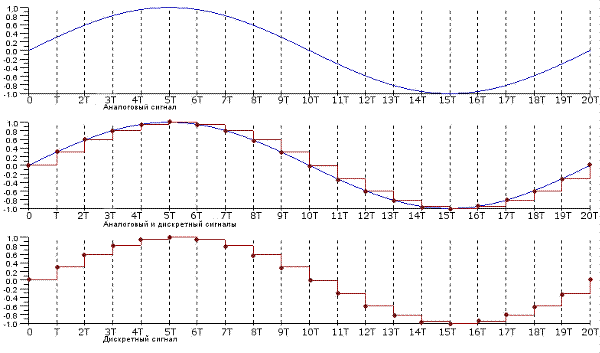
Рисунок 5 – Дискретизация прямоугольными импульсами
Запишем формулу (5) в общем виде, заменив дельта-функцию на функцию d (t), представляющую собой импульсы произвольной формы
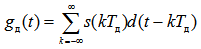(10)
Выражение (10) можно представить как прохождение сигнала (5) через линейную систему с импульсной характеристикой d (t). Поэтому спектр сигнала (10) будет связан со спектром сигнала (5) следующим образом
G д(ω) = D (ω) S д(ω) (11)
Тогда по (11) и (9) имеем
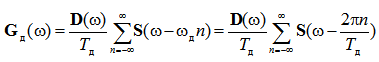(12)
Таким образом, отличие дискретизирующих импульсов от дельта-функции искажают спектр дискретного сигнала. Функция спектральной плотности импульса с конечной энергией убывает с ростом частоты, поэтому сдвинутые копии спектра сигнала оказываются ослабленными.
Спектр дискретизирующего прямоугольного импульса с единичной амплитудой и длительностью равной периоду дискретизации T Д, как мы рассмотрели ранее представляет собой функцию вида sin(x)/ x
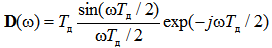(13)
Поэтому результирующий спектр цифрового сигнала дискретизированного прямоугольным импульсом оказывается взвешенным с функцией вида sin(x)/ x
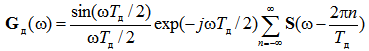(14)