. (14)
Если подставить вместо 
правые части исходной системы дифференциальных уравнений объекта:
k= 1 ,n- 1, (14а)
то
. (15)
А функционал с учетом (15) можно записать следующим образом:
. (16)
Из выражения (16) видно, что функционал характеризует некоторые свойства как исходного объекта, так и его системы управления в целом. При этом в данном методе оптимизирующий функционал не строго постулируется заранее, как это предполагается в стандартных задачах АКОР, а конструируется путем выбора соответствующих функций 
и 
с привлечением уравнений объекта, что позволяет учесть свойства исходного объекта. Метод синтеза управления на основе функционала (16) получил название аналитического конструирования агрегированных регуляторов (АКАР).
Агрегированные макропеременные Y выбираются из соображений, связанных с желаемыми переходными процессами и установившимися режимами движения объекта, степень близости которых проверяется обычно моделированием.
В терминах синергетики макропеременные - это задаваемые параметры порядка, путем оптимизации которых можно добиваться желаемого поведения динамических систем. Они определяют протекание процессов самоорганизации в синтезируемых системах. А отношение весовых коэффициентов g= m/c = 1/T функционала следует рассматривать как управляющие параметры.
Под эффективностью системы в синергетике понимают скорость изменения так называемой меры макроскопического действия при изменении управляющих параметров, равную квадрату параметра порядка. Эту меру также называют работой, производимой системой. Аналогом меры, таким образом, является 
, а эффективность системы 
. Изменяя параметр g и, следовательно, время движения ИТ к многообразию 
= 0, можно добиться желаемой эффективности синтезируемой системы.
Скалярное управление
Постановка задачи: требуется найти закон управления u(Y) = u(x1,...,xn), который обеспечивает перевод изображающей точки (ИТ) системы из произвольного начального состояния X 0 (x1,...,xn), (в некоторой допустимой области) сначала в окрестность многообразия Y(x1,...,xn) =0 в пространстве координат x 1 ,...,xn, а затем дальнейшее движение ИТ вдоль этого многообразия в начало координат пространства состояний. При этом на траекториях движения сохраняется минимум сопровождающего функционала (13).
Для решения задачи используется уравнение Эйлера-Лагранжа:
.
Подставляя в это выражение вместо 
его выражение из (13) находим, что уравнения экстремалей, доставляющих минимум функционалу имеют вид:
.
Это выражение включает в себя подсемейства устойчивых и неустойчивых экстремалей. Очевидно, что подсемейство устойчивых экстремалей, необходимое нам по условиям задачи синтеза, можно записать в виде следующего дифференциального уравнения:
, (17)
где Т = с/m.
Условие асимптотической устойчивости в целом этого уравнения относительно многообразия Y= 0 имеет простейший вид Т> 0.
Из уравнения (17) с учетом выражения (14) в силу исходных уравнений объекта получим следующее основное функциональное уравнение
. (18)
Отсюда
, (19)
которое определяет множество допустимых законов управления 
, обеспечивающих перевод ИТ из произвольного начального состояния в окрестность многообразия Y = 0. Законы управления (19) удерживают ИТ в этой окрестности при ее дальнейшем движении вдоль 
. Это движение уже будет описываться системой дифференциальных уравнений размерности (п- 1 ).
i = 1, n- 1 (20)
Для получения уравнения (5.23) следует из конечного уравнения 
=0 найти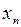 
и подставить его в первые (п- 1 ) уравнения объекта (14а).
Притягивающие многообразия могут быть интерпретированы как задаваемые целевые множества, к которым неизбежно должна притягиваться ИТ из произвольного начального состояния, а затем двигаться в соответствии с уравнениями (20) вдоль него. В связи с этим возникает задача исследования устойчивости движения ИТ вдоль многообразия y = 0, которое описывается системой (20).
Для целого класса распространенных объектов, в частности, имеющих треугольную матрицу функции y конструируются в результате регулярной процедуры, исходя из требований по времени и характеру (апериодическому) затухания переходных процессов и асимптотической устойчивости в целом синтезируемой системы.
Приближенные оценки времени движения ИТ из произвольного начального состояния в окрестность многообразия y = 0 определяются функциональным уравнением (5.20) и зависят от вида функции j(Y). При
(21)
уравнение (4.20) имеет вид
. (22)
Его решение
Y(t) = 
e-t/T. (23)
Отсюда время затухания функции от ее начального значения Y о до конечного Yк может быть найдено по формуле
t = 
. (24)
Если принять Yк = ( 0.01- 0.02 ) Y о, то получим
t @ ( 4 - 5 )T. (25)
Эта оценка определяет время попадания ИТ в окрестность многообразия =0.
Если в качестве j(Y) выбирается ограниченная функция
, (26)
так что при Y ® ± ¥, 
® ±1, а при малых Y, = Y, функциональное уравнение (5.20) принимает вид:
.
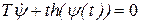Его решение
. (27)
Из него получим время затухания
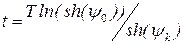. (28)
Приняв 
,где x = 0.01-0.02, получим
. (29)
Из уравнения (29) видно, что t является функцией граничных условий, в то время как оценка (24) остается неизменной для любых начальных условий. При этом в конце управления по истечении времени t (5.33) ИТ будет находиться в более близкой окрестности многообразия =0. Это следует из того, что в пределе функцию th(Y(t)) можно представить релейной функцией 
. Тогда уравнение (5.20) переходит в предельную форму
,
и ИТ сближается с многообразием Y(t) = 0 не за теоретически бесконечное время, как это следует из решений (5.28) и (5.33), а за определенное конечное время t = T|Yo|, зависящее от начальных условий, и теоретически точно попадает на притягивающее многообразие, в отличие от (5.28) и (5.33), для которых ИТ приближенно через время t попадает лишь в окрестность многообразия Y(t) = 0.
Пример 5.3.
Осуществим синтез управления объектом методом АКАР с передаточной функцией третьего порядка при переводе его из произвольного начального состояния в начало координат фазового пространства
.
Полагая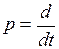 
, запишем систему дифференциальных уравнений, описывающих объект:
В качестве агрегированной макропеременной введем функцию в виде линейной комбинации фазовых координат:
.
Подставляя выражение (4.35) в уравнение (19) и полагая Т=1, а 
, получим следующее выражение для закона управления:
.
Эти законы управления обеспечивают движение изображающей точки в фазовом пространстве системы в окрестность многообразия 
. Дифференциальные уравнения, описывающие движение вдоль него, имеют вид:
или в виде одного дифференциального уравнения
.
Корни его характеристического уравнения равны
.
Система асимптотически устойчива в целом, если вещественная часть корней отрицательна. Рис.3 иллюстрирует на фазовой плоскости результаты моделирования системы с полученным управлением при k 2=2 и k 1=0.5. Объект переводится из заданного начального состояния х 0 ( 20,0,0 ) в начало координат фазового пространства.
Сравним характер движения ИТ на фазовой плоскости, если 
. В этом случае закон управления, полученный в соответствии с уравнением будет иметь вид:
.
Результаты моделирования представлены на рис.3а, б, в.
Из рисунка 3б видно, что в конце управления по истечении времени t (5.33) ИТ будет действительно находиться в более близкой окрестности многообразия 
=0.
На рис.3в представлен переходный процесс с этим же управлением.
а.
б.
в.
Рис.3 Результаты моделирования процессов на фазовой плоскости в системе с управлением при 
(рис.5.2а) и при 
(рис.5.2б, кривая в координатах у1-у2)