По определению суммы ряда 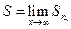 следовательно, при всех достаточно больших n разность
следовательно, при всех достаточно больших n разность  . Обозначим
. Обозначим  Величина
Величина  называется остатком ряда и сама является рядом.
называется остатком ряда и сама является рядом.
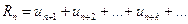
Взяв  и отбросив
и отбросив  , допускаем погрешность
, допускаем погрешность  которая называется остаточной погрешностью. Каждый член ряда будет вычисляться приближенно, поэтому при вычислении частичной суммы
которая называется остаточной погрешностью. Каждый член ряда будет вычисляться приближенно, поэтому при вычислении частичной суммы 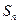 получим погрешность
получим погрешность  , которая называется погрешность промежуточных вычислений. Если каждый член ряда вычислять с точностью до знаков, т.е. с точностью до
, которая называется погрешность промежуточных вычислений. Если каждый член ряда вычислять с точностью до знаков, т.е. с точностью до  , то суммарная погрешность промежуточных вычислений
, то суммарная погрешность промежуточных вычислений  будет равна
будет равна  . Кроме того возможна погрешность начальных данных
. Кроме того возможна погрешность начальных данных  однако мы в дальнейшем будем считать
однако мы в дальнейшем будем считать  . Общая погрешность
. Общая погрешность  Обычно выбирают
Обычно выбирают  равными
равными  Иногда погрешностью промежуточных вычислений пренебрегают и считают
Иногда погрешностью промежуточных вычислений пренебрегают и считают 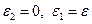 .
.
Наибольшую трудность вызывают оценка остаточной погрешности. Поскольку остаточный член  является рядом и точно вычислить его почти никогда не представляется возможным, то абсолютную величину остаточного члена оцениваю сверху. Если, начиная с некоторого номера
является рядом и точно вычислить его почти никогда не представляется возможным, то абсолютную величину остаточного члена оцениваю сверху. Если, начиная с некоторого номера  то отбрасывая все члены ряда, начиная с n + 1, получим остаточную погрешность не превосходящую
то отбрасывая все члены ряда, начиная с n + 1, получим остаточную погрешность не превосходящую  . Выбрав таким образом n, подбирают k так чтобы выполнялось неравенство
. Выбрав таким образом n, подбирают k так чтобы выполнялось неравенство  , а затем проводят вычисления. В результате сумма ряда будет найдена с заданной точностью
, а затем проводят вычисления. В результате сумма ряда будет найдена с заданной точностью  .
.
Умножим некоторые способы оценки остаточного члена.
a) Если рад является знакочередующимся 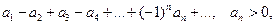 то в силу следствия из теоремы Лейбница.
то в силу следствия из теоремы Лейбница.
 (1.39)
(1.39)
т.е. абсолютная величина остаточного члена не превосходит абсолютной величины первого отброшенного члена.
Пример 1. Найти сумму ряда

то с точностью до 
Выбираем 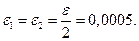
В силу формулы (1.39)

Подберем n так, чтобы выполнялось неравенство  , т.е.
, т.е.  . Наименьшее значение n, при котором выполняется это неравенство, равно 44
. Наименьшее значение n, при котором выполняется это неравенство, равно 44  Таким образом, чтобы остаточная погрешность не превосходила 0,0005, достаточно взять сумму первых 44 членов ряда, а члены ряда, начиная с 45-го, отбросить. Определим теперь, с какой точностью нужно вести промежуточные вычисления. Для этого нужно выбрать k так, чтобы выполнялось неравенство
Таким образом, чтобы остаточная погрешность не превосходила 0,0005, достаточно взять сумму первых 44 членов ряда, а члены ряда, начиная с 45-го, отбросить. Определим теперь, с какой точностью нужно вести промежуточные вычисления. Для этого нужно выбрать k так, чтобы выполнялось неравенство

Достаточно взять  . Заметим, что при
. Заметим, что при  неравенство не выполняется (многие считают, что, если какую – либо величину нужно вычислить с точностью до трех знаков, то промежуточные вычисления нужно вести с точностью до четырех знаков, а затем округлить до трех знаков. Как видно из этого примера, такое утверждение неверно). Итак,
неравенство не выполняется (многие считают, что, если какую – либо величину нужно вычислить с точностью до трех знаков, то промежуточные вычисления нужно вести с точностью до четырех знаков, а затем округлить до трех знаков. Как видно из этого примера, такое утверждение неверно). Итак,
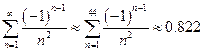
б) Рассмотрим ряд с положительными членами (1.1)  . Предположим, что не возрастают
. Предположим, что не возрастают 
и  - невозрастающая, непрерывная функция такая, что
- невозрастающая, непрерывная функция такая, что  . Тогда
. Тогда

Пример 2. Оценить остаточный член ряда.

Рассмотрим функцию 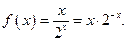 Тогда
Тогда 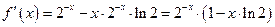 . При
. При  следственно функция монотонно убывает при
следственно функция монотонно убывает при 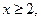 а поэтому члены ряда
а поэтому члены ряда 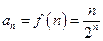 монотонно убывают при
монотонно убывают при  Таким образом
Таким образом

Поскольку  (в последнем можно убедится, правило Лопиталя), то
(в последнем можно убедится, правило Лопиталя), то

Пример 3. Вычислить сумму ряда.
 (1.40)
(1.40)
с точностью до 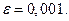
Возьмём  . Здесь
. Здесь 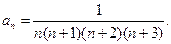 Легко убедится что
Легко убедится что

Функция 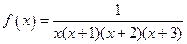 - непрерывная при
- непрерывная при  и монотонно убывающая, поэтому
и монотонно убывающая, поэтому
 (1.41)
(1.41)
Поскольку  , то
, то

Если выбрать n так, чтобы выполнялось неравенство  то тем более будет выполнятся неравенство
то тем более будет выполнятся неравенство 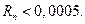 Найдём это n:
Найдём это n:

Наименьшее целое значение n, при котором выполняется это неравенство, равно 6.
Таким образом, 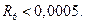 (Отметим, что, если в неравенстве (1.40) подыинтегральную дробь размножить на простейшие и вычислить интеграл, то возможно, что при n = 5 значение интеграла будет меньше 0,0005, и тогда было бы
(Отметим, что, если в неравенстве (1.40) подыинтегральную дробь размножить на простейшие и вычислить интеграл, то возможно, что при n = 5 значение интеграла будет меньше 0,0005, и тогда было бы  но вряд ли целесообразно выполнять эти длинные вычисления из-за одного слагаемого). Промежуточные вычисления будем выполнять с точностью до 5 знаков:
но вряд ли целесообразно выполнять эти длинные вычисления из-за одного слагаемого). Промежуточные вычисления будем выполнять с точностью до 5 знаков: 
Вычислим сумму ряда с точностью до 0,001:
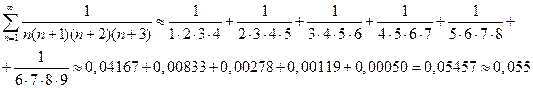
в) На следующем примере продемонстрируем искусственный метод оценки остаточного члена.
Пример 4. Сколько членов ряда  нужно взять, чтобы остаточный член был меньше
нужно взять, чтобы остаточный член был меньше 
Оценим остаточный член ряда сверху:

В последних скобках записан геометрический ряд, первый член которого равен 1, а знаменатель  поэтому
поэтому
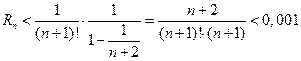
Наименьшее целое значение n, при котором выполняется последнее неравенство, равно 6. Итак, 
II. ФУНКЦИОНАЛЬНЫЕ РЯДЫ.