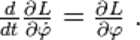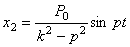 .
.
Так как 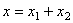 , а общее решение имеет окончательно вид
, а общее решение имеет окончательно вид
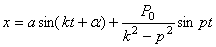 ,
,
где а и 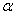 - постоянные интегрирования, определяемые по начальным данным. Решение показывает, что колебания точки складываются в этом случае из: 1) колебаний с амплитудой а (зависящей от начальных условий) и частотой k, называемых собственными колебаниями, и 2) колебаний с амплитудой А (не зависящей от начальных условий) и частотой р, которые называются вынужденными колебаниями
- постоянные интегрирования, определяемые по начальным данным. Решение показывает, что колебания точки складываются в этом случае из: 1) колебаний с амплитудой а (зависящей от начальных условий) и частотой k, называемых собственными колебаниями, и 2) колебаний с амплитудой А (не зависящей от начальных условий) и частотой р, которые называются вынужденными колебаниями
Частота р вынужденных колебаний, как видно, равна частоте возмущающей силы. Амплитуду этих колебаний, если разделить числитель и знаменатель на 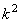 , можно представить в виде:
, можно представить в виде:
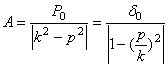 ,
,
где 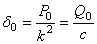 , т. е.
, т. е. 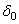 есть величина статического отклонения точки под действием силы
есть величина статического отклонения точки под действием силы 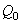 . Как видим, A зависит от отношения частоты р возмущающей силы к частоте k собственных колебаний.
. Как видим, A зависит от отношения частоты р возмущающей силы к частоте k собственных колебаний.
Подбирая различные соотношения между р и k, можно получить вынужденные колебания с разными амплитудами. При 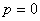 амплитуда равна
амплитуда равна 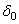 (или близка к этой величине). Если величина р близка к k, амплитуда A становится очень большой. Когда
(или близка к этой величине). Если величина р близка к k, амплитуда A становится очень большой. Когда 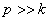 , амплитуда A становится очень малой (практически близка к нулю).
, амплитуда A становится очень малой (практически близка к нулю).
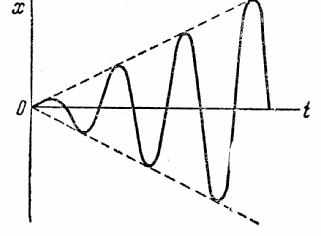
Резонанс. В случае, когда 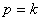 , т.е. когда частота возмущающей силы равна частоте собственных колебаний, имеет место так называемое явление резонанса. Размахи вынужденных колебаний при резонансе будут со временем неограниченно возрастать так, как показано на рис.35.
, т.е. когда частота возмущающей силы равна частоте собственных колебаний, имеет место так называемое явление резонанса. Размахи вынужденных колебаний при резонансе будут со временем неограниченно возрастать так, как показано на рис.35.
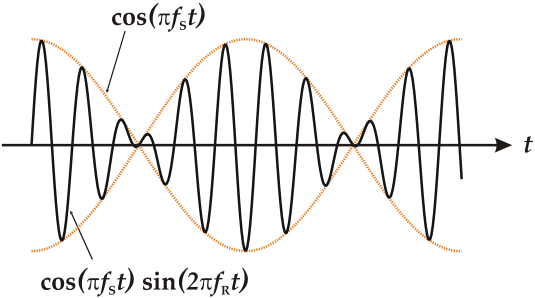
Биения — явление, возникающее при наложении двух гармонических колебаний, выражающееся в периодическом уменьшении и увеличении амплитуды суммарного сигнала. Биения модулируются по амплитуде. Распространение такого вида колебаний менее эффективно. Частота изменения амплитуды суммарного сигнала равна разности частот двух исходных сигналов.
10) Вынужденные колебания при наличии трения.
Исследование вынужденных колебаний при наличии трения вполне аналогично произведенному здесь рассмотрению колебаний без трения. Мы остановимся здесь подробно на представляющем самостоятельный интерес случае периодической вынуждающей силы.
Прибавив в правой части уравнения (25.1) внешнюю силу ƒcos  t и разделив на m, получим уравнение движения в виде
t и разделив на m, получим уравнение движения в виде
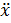 + 2λ
+ 2λ 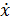 +
+ 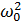 x =
x = 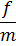 cos
cos  t. (26.1)
t. (26.1)
Решение этого уравнения удобно находить в комплексной форме, для чего пишем в правой части ei 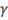 t вместо cos
t вместо cos  t:
t:
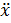 + 2λ
+ 2λ 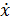 +
+ 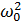 x =
x = 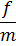 ei
ei 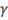 t .
t .
Частный интеграл ищем в виде х = Вегу1 и находим для В:
B = 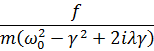 .
.
Представив B в виде beiδ, имеем для b и δ:
b = 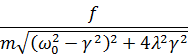 , tg δ =
, tg δ = 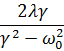 . (26.3)
. (26.3)
Наконец, отделив вещественную часть от выражения Bei 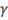 t = b
t = b 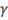 t +δ) получим частный интеграл уравнения (26.1), а прибавив к нему общее решение уравнения без правой части (которое мы напишем для определенности для случая ω0>λ), получим окончательно:
t +δ) получим частный интеграл уравнения (26.1), а прибавив к нему общее решение уравнения без правой части (которое мы напишем для определенности для случая ω0>λ), получим окончательно:
x = α e −λ t cos (ω t + 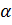 ) + b cos (λ t + δ). (26.4)
) + b cos (λ t + δ). (26.4)
Первое слагаемое экспоненциально убывает со временем, так что через достаточно большой промежуток времени остается только второй член:
x = b cos ( t + δ). (26.5)
t + δ). (26.5)
Выражение (26.3) для амплитуды b вынужденного колебания хотя и возрастает при приближении частоты  к ω0, но не обращается в бесконечность, как это было при резонансе в отсутствие трения. При заданной амплитуде силы ƒ амплитуда колебания максимальна при частоте
к ω0, но не обращается в бесконечность, как это было при резонансе в отсутствие трения. При заданной амплитуде силы ƒ амплитуда колебания максимальна при частоте  =
= 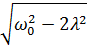 ; при λ<<ω0 это значение отличается от ω0 лишь на величину второго порядка малости.
; при λ<<ω0 это значение отличается от ω0 лишь на величину второго порядка малости.
Рассмотрим область вблизи резонанса. Положим  =ω0+ε, где ε — малая величина; будем также считать, что λ<<ω0. Тогда в (26.2) можно приближенно заменить:
=ω0+ε, где ε — малая величина; будем также считать, что λ<<ω0. Тогда в (26.2) можно приближенно заменить:
 2 −
2 − 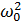 = (
= ( + ω0)(
+ ω0)( − ω0) ≈ 2ω0ε, 2 i λ
− ω0) ≈ 2ω0ε, 2 i λ  ≈ 2 i λω0,
≈ 2 i λω0,
так что
B = − 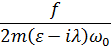 (26.6)
(26.6)
или
b = 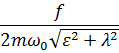 , tg δ =
, tg δ =  . (26.7)
. (26.7)
Отметим характерную особенность хода изменения разности фаз δ между колебанием и вынуждающей силой при изменении частоты последней. Эта разность всегда отрицательна, т.е. колебание «запаздывает» относительно внешней силы. Вдали от резонанса, со стороны  <ω0, δ стремится к нулю, а со стороны
<ω0, δ стремится к нулю, а со стороны  >ω0 — к значению −
>ω0 — к значению − 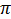 . Изменение δ от нуля до −
. Изменение δ от нуля до − 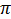 происходит в узкой (ширины ~λ) области частот, близких к ω0; через значение −
происходит в узкой (ширины ~λ) области частот, близких к ω0; через значение − 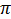 /2 разность фаз проходит при
/2 разность фаз проходит при  =ω0. Отметим в этой связи, что в отсутствие трения изменение фазы вынужденного колебания на величину
=ω0. Отметим в этой связи, что в отсутствие трения изменение фазы вынужденного колебания на величину 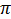 происходит скачком при
происходит скачком при  =ω0 (второй член в (22.4) меняет знак); учет трения
=ω0 (второй член в (22.4) меняет знак); учет трения
«размазывает» этот скачок.
При установившемся движении, когда система совершает вынужденные колебания (26.5), ее энергия остается неизменной. В то же время система непрерывно поглощает (от источника внешней силы) энергию, которая диссипируется благодаря наличию трения. Обозначим через I ( ) количество энергии, поглощаемой в среднем в единицу времени, как функцию частоты внешней силы. Согласно (25.13) имеем
) количество энергии, поглощаемой в среднем в единицу времени, как функцию частоты внешней силы. Согласно (25.13) имеем
I ( ) = 2
) = 2 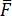 ,
,
где 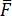 — среднее (по периоду колебания) значение диссипативной функции. Для одномерного движения выражение (25.11) диссипативной функции сводится к F =
— среднее (по периоду колебания) значение диссипативной функции. Для одномерного движения выражение (25.11) диссипативной функции сводится к F = 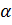
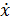 2 /2 = λ m
2 /2 = λ m 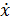 2. Подставив сюда (26.5), получим
2. Подставив сюда (26.5), получим
F = λ mb 2  2 sin2 (
2 sin2 ( t + δ).
t + δ).
Среднее по времени значение квадрата синуса равно 1/2, поэтому
I ( ) = λ mb 2
) = λ mb 2  2. (26.8)
2. (26.8)
Вблизи резонанса, подставляя амплитуду колебания из (26.7), имеем
I (ε) = 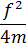
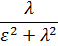 . (26.9)
. (26.9)
Такой вид зависимости поглощения от частоты называется дисперсионным. Полушириной резонансной кривой (рис. 31) называют значение |ε|, при котором величина I (ε) уменьшается вдвое по сравнению с ее максимальным значением при ε=0.
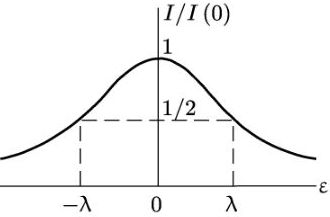
Рис. 31
Из формулы (26.9) видно, что в данном случае эта ширина совпадает с показателем затухания λ. Высота же максимума
I (0) = 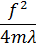
обратно пропорциональна λ. Таким образом, при уменьшении показателя затухания резонансная кривая становится уже и выше, т.е. ее максимум становится более острым. Площадь же под резонансной кривой остается при этом неизменной.
Последняя дается интегралом
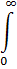 I (
I ( ) d
) d  =
= 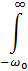 I (ε) d ε.
I (ε) d ε.
Поскольку I (ε) быстро убывает при увеличении |ε|, так что область больших |ε| все равно не существенна, можно при интегрировании писать I (ε) в виде (26.9), а нижний предел заменить на − 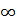 . Тогда
. Тогда
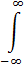 I (ε) d ε =
I (ε) d ε = 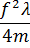
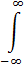
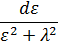 =
= 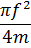 . (26.10)
. (26.10)
11) Вынужденные колебания при наличии трения.
Если точка подвеса достаточно быстро колеблется вверх-вниз, то маятник приобретает устойчивое положение «вверх тормашками, блядь». Такая система называется маятником Капицы.
Маятником Капицы называется система, состоящая из грузика, прикрепленного к легкой нерастяжимой спице, которая крепится к вибрирующему подвесу. При неподвижной точке подвеса, модель описывает обычный математический маятник, для которого имеются два положения равновесия: в нижней точке и в верхней точке. При этом равновесие математического маятника в верхней точке является неустойчивым, и любое сколь угодно малое возмущение приводит к потере равновесия.
Удивительной особенностью маятника Капицы является то, что вопреки интуиции перевернутое (вертикальное) положение маятника может быть устойчивым в случае быстрых вибраций подвеса. Капица экспериментально исследовал такой маятник, а также построил теорию динамической стабилизации, разделяя движение на «быстрые» и «медленные» переменные и введя эффективный потенциал.
Маятник Капицы интересен еще и тем, что в такой простой системе можно наблюдать параметрические резонансы, когда нижнее положение равновесия не является больше устойчивым и амплитуда малых отклонений маятника нарастает со временем.
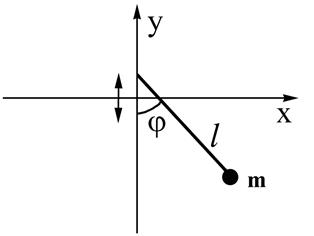
Направим ось 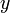 вертикально вверх, а ось
вертикально вверх, а ось 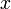 горизонтально, так чтобы плоское движение маятника происходило в плоскости (
горизонтально, так чтобы плоское движение маятника происходило в плоскости (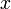 —
— 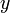 ). Введем обозначения:
). Введем обозначения:
§  — частота вынуждающих вертикальных гармонических колебаний подвеса,
— частота вынуждающих вертикальных гармонических колебаний подвеса,
§ 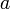 — амплитуда вынуждающих колебаний,
— амплитуда вынуждающих колебаний,
§ 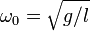 — собственная частота колебаний математического маятника,
— собственная частота колебаний математического маятника,
§ 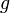 — ускорение свободного падения,
— ускорение свободного падения,
§ 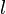 — длина легкого стержня,
— длина легкого стержня,
§  — масса грузика.
— масса грузика.
Если угол между стержнем и осью 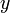 обозначить как
обозначить как  , то зависимость координат грузика от времени запишется следующими формулами:
, то зависимость координат грузика от времени запишется следующими формулами:
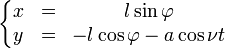
Движение маятника удовлетворяет уравнениям Эйлера — Лагранжа. Зависимость фазы маятника  от времени определяет положение грузика[5]:
от времени определяет положение грузика[5]: