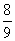The usefulness of linear programming as a tool for optimal decision making and resource allocation is based on its applicability to many business problems. The effective use and application of linear programming require, as a first step, the formulation of the model when the problem is presented. Several examples are given in this section to illustrate the formulation of linear programming problems.
Example 2-1. A furniture manufacturer.
A small furniture manufacturer produces thee different kinds of furniture: desks, chairs, and bookcases. The wooden materials have to be cut properly by machines. In total, 100 machine-hours are available for cutting. Each unit of desks, chairs, and bookcases requires 0.8 machine-hour, 0.4 machine-hour, and 0.5 machine-hour, respectively.
This manufacturer also has 650 man-hours available for painting and polishing. Each unit of desks, chairs, and bookcases requires 5 man-hours, 3 man-hours, and 3 man-hours for painting and polishing, respectively. These products are to be stored in a warehouse which has a total capacity of 1.260 sq. ft. The floor space required by these three products are 9 sq ft, 6 sq ft, and 9 sq ft, respectively, per unit of each product. In the market, each product is sold at a profit of $30, $16, and $25 per unit, respectively. How many units of each product should be made, to realize a maximum profit?
Formulation of Example 2-1. Let x1, x2, x3 be the number of units of desks, chairs, and bookcases to be produced, respectively. Since 100 total machine-hours are available for cutting, the production of x1, x2, and x3 should utilize no more than the available machine-hours. Therefore, the mathematical statement of the first side constraint is in the form:
0.8x1 + 0.4x2 + 0.5x3 ≤ 100
Also, no more than 650 man-hours and 1.260 sq ft are available for painting and polishing and storing, respectively. Therefore, these two side constraints are in the form:
5x1 + 3x2 + 3x3 ≤ 650
9x1 + 6x2 + 9x3 ≤ 1.260
Finally, the decision variable must be nonnegative.
The problem them can be formulated as follows:
Maximize
F = 30x1 + 16x2 + 25x3
subject to
0.8x1 + 0.4x2 + 0.5x3 ≤ 100
5x1 + 3x2 + 3x3 ≤ 650
9x1 + 6x2 + 9x3 ≤ 1.260
and x1 ≥ 0, x2 ≥ 0, x3 ≥ 0
Example 2-2. The riverside rubber company
The Riverside Rubber Company specializes in the production of three different kinds of tires: premium tires, deluxe tires, and regular tires. These three different tires are produced at the company’s two different plants, with different production capacities. In a normal 8-hours working day, Plant A produces 50 premium tires, 80 deluxe tires, and 100 regular tires. Plant B produced 60 premium tires, 60 deluxe tires, and 200 regular tires. The monthly demand for each of these is know to be 2,500 units, 3,000 units, and 7,000 units, respectively. The company finds that the daily cost of operation is $2,500 in Plant A and $3,500 in Plant B.
Find the optimum number of days of operations per month at the two different plants to minimize the total cost while meeting the demand.
Formulation of Example 2-2. Let the decision variables x1 and x2 represent the number of days of operation in each of these plants. The objective function of this problem is the sum of the daily operational costs in the two different plants; that is,
Z = 2,500x1 + 3,500x2
Given the total revenue, the profit is increased by reducing the total cost. The objective, then, is to determine the value of the decision variables x1 and x2, which yield the minimum of total cost subject to side constraints. The production of each of three different tires must be at least equal to or greater than the specific quantity in order to meet the demand requirement. In no event should the production be less than the quantities of each product demanded.
Together with the side constraints, the problem then can be formulated as:
Minimize
Z = 2,500x1 + 3,500x2
Subject to
50x1 + 60x2 ≥ 2,500
80x1 + 60x2 ≥ 3,000
100x1 + 200x2 ≥ 7,000
and x1 ≥ 0, x2 ≥ 0.
Example 2-3 A local auto shop. A local auto shop needs 400 cans of paints per month, the supply consisting of three different colors. The cost per can of each of these is given as follows:
Blue $4.00 per can
Brown $4.50 per can
Black $4.25 per can
The auto-repair work requires at least 80 cans of brown paint, not more than 160 cans of blue paint, and at least 40 cans of black paint. How many cans of each of these paints should be purchased to minimize the total cost?
Formulation of Example 2-3 To set up this situation as a linear programming problem, an objective function stated in terms of cost is required. Let the decision variables x1, x2 and x3 represent the number of cans of blue paint, and black paint required, respectively. Then, the objective function is expressed as
Z = 4.000x1 + 4.50x2 + 4.25x3
Naturally, the value of this function must be minimized, subject to the monthly requirement constraints.
Since the auto-repair work does not require more than 160 cans of blue paint, x1 must be less than or equal to 160 cans,
x1 ≤ 160
The direction of inequality sings of the second and the third constraints is different from that of the first, because the auto-repair work requires at least 80 cans of brown paint and 40 cans of black paint. Hence
x2 ≥ 80
x3 ≥ 40
The final constraint is specified by the fact that the monthly requirement of these paints is 400 cans.
x1 + x2 + x3 = 400
The problem is then summarized in the general linear programming form as
Minimize
Z = 4.00x1 + 4.50x2 + 4.25x3
Subject to
x1 ≤ 160
x2 ≥ 80
x3 ≥ 40
x1 + x2 + x3 = 400
x1 ≥ 0, x2 ≥ 0, x3 ≥ 0
(In this particular problem, the two nonnegative constraints x2 ≥ 0 and x3 ≥ 0 may be redundant)
Example 2-4
THE TIFFANY INVESTMENT COMPANY The Tiffany Investment Company possesses a large amount of cash to invest – say, $1,000,000. There are five different investment choices, each with different growth and income potentialities: common stocks, mutual funds, municipal bonds, saving certificates, and real estate investments. The current returns from the investment of each of these five choices are also different. The current returns on investment are known for each of the investment opportunities as follows:
Current annual yield percent
| Common stocks
|
| | Mutual funds
|
| | Municipal bonds
|
| | Savings certificates
|
| | Real estate investment
|
| In this case, management believes that the current yield will persist in the future and wishes to diversify the investment portfolio of the company to obtain maximum returns. Because of the risk element involved, management restricts the investment in common stocks to not more than the combined total investment in municipal bonds, savings certificates, and real estate investment. Total investment in mutual funds and real estate combined must be at least as large as that in municipal bonds. Also, management wishes to restrict its investment in mutual funds to a level not exceeding that of savings certificates. Determine the optimum allocation of investment funds among these five choices and the actual amount of returns from investment under the above conditions.
Formulation of Example 2-4 In this investment problem, the decision that needs to be made concerns how to allocate the available investment funds into the various alternative choices. In this instance, there are five decision variables. Let the decision variables x1, x2, x3, x4, and x5 represent the percentage of the total investment fund to be allocated into common stocks, mutual funds, municipal bonds, savings certificates, and real estate investment, respectively. Then the objectives is to maximize the total returns from the different investment choices. The objective function is
F = 0.10x1 + 0.08x2 + 0.06x3 + 0.05x4 + 0.09x5
As mentioned earlier, the side constraints must be linear inequalities of the decision variables. The first side constraint comes from the restriction of investment in common stocks to not more than the combined total investment in municipal bonds, savings certificates, and real estate investment. This restriction can be expressed in a linear inequality form
x1 ≤ x3 +x4 + x5
The second side constraint comes from the restriction that total investment in mutual funds and real estate combined must be at leats as large as that in municipal bonds.
Formulation of Example 2-4 In this investment problem, the decision that needs to be made concerns how to allocate the available investment funds into the various alternative choices.
Formulation of Example 2-4
In this investment problem, the decision that needs to be made concerns how to allocate the available investment funds into the various alternative choices. In this instance, there are five decision variables. Let the decision variables x1, x2, x3, x4, and x5 represent the percentage of the total investment fund to be allocated into common stocks, mutual funds, municipal bonds, savings certificates, and real estate investment, respectively. Then the objective is to maximize the total returns from the different investment choices. The objective function is
F=0,01x1+0,08x2+0,06x3+0,05x4+0,09x5
As mentioned earlier, the side constraints must be linear inequalities of the decision variables. The first side constraint comes from the restriction of investment in common stocks to not more than the combined total investment in municipal bonds, savings certificates, and real estate investment. This restriction can de expressed in a linear inequality form
x1 ≤ x3+x4+x5
The second side constraint comes from the restriction that total investment in mutual funds and real estate combined must be at least as large as that in municipal bonds.
x2+x3≥x3
The third side constraint is the fact that the restriction of investment in savings certificates.
x2≤x4
Finally, the aggregate of total investment in different choices must be equal to 1; that is 100 (or $1 million).
x1+x2+x3+x4+x5=1
Here is the problem, summarized in linear programming form, together with the conditions of nonnegativity:
Maximize
F=0,01x1+0,08x2+0,06x3+0,05x4+0,09x5
subject to
x1≤x3+x4+x5
x2+x3≥x3
x2≤x4
x1+x2+x3+x4+x5=1
and
x1≥0,x2≥0,x3≥0,x4≥0,x5≥0
2-6 Graphic representation linear programming problem can easily be solved by a graphic method when it involves two decision variables. It is also possible to solve a linear programming problem with three decision variables by a graphic method. But its presentation is not as easy as in the problem with two decision variables, because it requires three dimensions to illustrate. A graphic method is not practical when there are more than three decision variables, because there is no way of presenting more than three dimensions in space.
2-6.1 A Maximization Problem
To illustrate the graphic method, let us again consider the Riggs Manufacturing Company’s production problem as given in Sec. 2-2. The problem is summarized in a linear programming form:
Maximize
F = 50x1 + 80x2
subject to
x1 ≤ 80 (Assembly Line I)
x2 ≤ 60 (Assembly Line II)
5x1 + 6x2 ≤ 600 (electronic components)
x1 + 2x2 ≤ 160 (labor supply)
and x1 ≥ 0, x2 ≥ 0
where x1= number of regular television sets to be produced
x2= number of color television sets to be produced
Assembly-line constraints
Let us draw a two-dimensional graph, with the production of regular television sets shown on the horizontal axis and the production of color television sets shown on the vertical axis.
Because of the limited capacity in Assembly Line I, where regular television sets are produced, no more than 80 units of x1 can be produced per day; that is, x1≤80. The side constraint for Assembly Line I consists of two parts: an equality part and an inequality part. Thus, the number of the regular television sets assembled will be either x1=80 or x1<80. Together with the nonnegativity condition x1≥0, the inequality side constraint for Assembly Line I can be represented by the shaded area shown in Fig. 2-1.
A daily production of color television sets is limited to 50 units when Assembly Line II is fully utilized; that is, x2≤50. As in the case of Assembly Line I, together with the nonnegativity condition, the inequality side constraint for Assembly Line II can be represented by a shaded area as shown in Fig. 2-2.
Figures 2-1 and 2-2 are combined to obtain an area which simultaneously satisfies the two assembly-line constraints. Then the production of x1 and x2 can be represented by the shaded rectangle area shown in Fig. 2-3.
Electronic-components constraint. The production of x1 and x2 is also limited by the available electronic components. The inequality
5x1+6x2≤600
 may be drawn by the line MM in Fig. 2-4. If the entire electronic components are used for the production of x1, 120 units of x1 can be produced. Similarly, if all the available components are used for the production of x2, 100 units of x2 can be produced. The line MM is drawn by connecting these two extreme points. Any point on the line MM indicates a different production program with full utilization of available electronic components. For example, at the point M1, the production combination of 30 units of x1 and 75 units of x2 is possible; at the point M2, 60 units of x1 and units of x2; at the point M3, 84 units of x1 and 30 units of x2. All these points lie on the straight line MM, because they indicate different production programs of x1 and x2 with full utilization of available electronic components. A different product combination is also possible on any points to the left of the line MM, but not to the right, because of the limited availability of electronic components. may be drawn by the line MM in Fig. 2-4. If the entire electronic components are used for the production of x1, 120 units of x1 can be produced. Similarly, if all the available components are used for the production of x2, 100 units of x2 can be produced. The line MM is drawn by connecting these two extreme points. Any point on the line MM indicates a different production program with full utilization of available electronic components. For example, at the point M1, the production combination of 30 units of x1 and 75 units of x2 is possible; at the point M2, 60 units of x1 and units of x2; at the point M3, 84 units of x1 and 30 units of x2. All these points lie on the straight line MM, because they indicate different production programs of x1 and x2 with full utilization of available electronic components. A different product combination is also possible on any points to the left of the line MM, but not to the right, because of the limited availability of electronic components.
Labor-supply constraint.
A similar procedure applies to the drawing of the labor-supply inequality constraint x1+2x2≤160. If all the available workers are fully employed for the production of regular television sets alone, 160 units of x1 will be produced per day. Similarly, 80 units of x2 will be produced per day when all the available workers produce only color television sets. The line LL in Fig. 2-5 is drawn by connecting these two extreme points.
Any point on the line LL represents all combinations of x1 and x2 with full utilization of available labor supply. The line LL divides the plane into two parts. Different combinations of x1 and x2 are possible in the lower-left part of the line LL, because all points in the left part satisfy the inequality constraint x1 + 2x2 < 160. All points in the upper-right part of the line LL cannot be considered, because they would be represented by the inequality x1 + 2x2 < 160. That is, all combinations of x1 and x2 in the upper-right part of the plane require more than 160 workers.
Since all these inequality constraints must be satisfied simultaneously, they are combined in Fig. 2-6. The shaded area, denoted by a hexagon OABCDE, is the area which satisfies all the side inequality constraints at the same time, as well as the nonnegative conditions. It is called the feasible region, or admissible region. All points in the shaded area, including the boundaries of the hexagon, are the only ones that satisfy all the restrictions and therefore are feasible. Consequently, all points outside the shaded area are not feasible.
Let us choose any two points Q and R to illustrate the production feasibility. Obviously, these two points lie outside the feasible region. At Q the production is not feasible because it violates the capacity restriction of Assembly Line I. Similarly. Point R is also not feasible, as it violates the electronic components’ supply restriction.
The next step is to find a point from this feasible region that maximize the value of the objective function, i.e. profits. In order to find this point let us consider an arbitrary case in which the daily profit is $2000. Then the objective function is 2.000 = 50x1 + 80x2. This equation is represented by a straight line P1 by connecting two extreme points, as shown in Fig. 2-7. Two extreme points are found by setting x2=0 and then x1=0.
If x2 = 0
2.000 = 50x1 + 80(0)
x1 = 40
And if x1 = 0
2.000 = 50(0) + 80x2
x2 = 25
And so all points on the line P1 yield a daily profit of $2,000 with different combinations of x1 and x2.
Let us consider another arbitrary case, in which the daily profit is $4,000. The objective function 4,000 = 50x1 + 80x2 is represented by a straight line P2 by connecting two extreme points x1 = 80 and x2 = 50. All points on the line P2 yield a daily profit of $4,000 with different combinations of x1 and x2. The line P2 is farther right from the origin and is parallel to the line P1, and so on. If we draw a new straight line P4, which is parallel to the line P1, and move as far as possible from the origin to the right, then the line P4 is tangent to one of the corner boundary points C. The lines P1, P2, P3, and P4 are known as profit contour lines, or isoprofit lines. Clearly, the line P4 is preferable to other profit contour lines P1, P2, and P3, because the largest profit is found on any point on this line. There is only one point C that lies on the line P4 and is in common with the feasible region. At this corner point C, where x1 = 60 and x2 = 50, the maximum daily profit of $7,000 is obtainable. The optimal solution, then, is to produce 60 units of regular television sets and 50 units of color television sets per day. The maximum profit obtainable is $7,000 per day.
To verify the optimal solution at Point C, we test the objective function F = 50x1 + 80x2 at each of the five corner points of the feasible region A, B, C, D, and E.
A: 50 (80) + 80 (0) = 4,000
B: 50 (80) + 80 ( 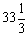 ) = 6,666 ) = 6,666 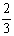
C: 50 (60) + 80 (50) = 7,000
D: 50 (40) + 80 (60) = 6,800
E: 50 (0) + 80 (60) = 4,800
Again, we see that the maximum daily profit of $7,000 is obtained at Point C.
The daily production of 60 regular television sets and 80 color television sets must satisfy the side constraints.
Assembly Line I: 60<80
Assembly Line II: 50<60
Electronic components:
5(60) + 6(50) = 600
Labor supply: 60 + 2(50) = 160
Thus, the available electronic components and labor force are fully utilized are point C. However, there is still the unutilized capacity to produce 20 regular television sets in Assembly Line I and 10 color television sets in Assembly Line II.
2-6.2 A Minimization Problem
A minimization problem of linear programming can also be solved by the graphic method. Let consider the problem of the Riverside Rubber Company, as described in Example 2-2, to illustrate the minimization problem.
The problem is stated in the linear programming form:
Minimize
Z = 2,500x1 + 3,500x2
Subject to
50x1 + 60x2 ≥ 2,500 (premium tires)
80x1 + 60x2 ≥ 3,000 (deluxe tires)
100x1 + 200x2 ≥ 7,000 (regular tires)
and x1 ≥ 0, x2 ≥ 0
where x1 = number of days of operation in Plant A
x2 = number of days of operation in Plant B
To simplify the computation, the three side constraints can be expressed in the reduced form. In doing this, both sides of the inequalities are divided by 10 in the first constraint, 20 in the second, and 100 in the third. Thus, we get
5x1 + 6x2 ≥ 250 (premium tires)
4x1 + 3x2 ≥ 150 (deluxe tires)
x1 + 2x2 ≥ 70 (regular tires)
The three constraints are represented in Fig. 2-8, following the same procedures discussed in the preceding section. It is to be noted that the side constraints in a minimization problem are by “greater than or equal to” (≥). They must be represented by all points on and to the right of the three lines (ABCD) drawn. Therefore, all combinations of x1 and x2 that simultaneously satisfy the three side constraints must fall on or to the right of the convex polyhedral set ABCD. This is the shaded area in Fig. 2-8, and represents the feasible region.
The four corner points of the feasible region are
A (70,0) B (20,25)
C ( 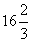 ,27 ,27  ) D (0,50) ) D (0,50)
To find the optimal solution, these four corner points are tested out with the objective function Z = 2,500x1 + 3,500x2.
A: 2,500 (70) + 3,500 (0) = 175,000
B: 2,500 (20) + 3,500 (25) = 127,500
C: 2500 (16 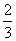 ) + 3,500 (27 ) + 3,500 (27  ) = 138,888 ) = 138,888 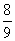
D: 2,500 (0) + 3,500 (50) = 175,000
Test results indicate that the minimum monthly operating cost of $127,000 is found at Point B. To achive this, the company must operate 20 days in Plant A and 25 days in Plant B per month.[2]
The monthly supply requirements are tested at Point B, substituting x1 = 20 and x2 = 25.
Premium tires: 50 (20) + 60 (25) = 2,500
Deluxe tires: 80 (20) + 60 (25) = 3,100
Regular tires: 100 (20) + 200 (25) = 7,000
We see that when two plants are operated as indicated, the company exactly meets the monthly supply requirements of 2,500 premium tires and 7,000 regular tires. There will be a surplus of 100 deluxe tires after meeting the supply requirements of 3,000 units, because the combined production of deluxe tires is 3,100 units at Point B.
|
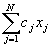 subject to
subject to
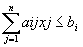 (for i =1, 2,…, m)
and xj ≥ 0 (for j = 1, 2, …, n)
where Σ= Greek letter capital sigma, which means “the sum of”.
The above problem is formulated in a more general form:
Minimize Z=
(for i =1, 2,…, m)
and xj ≥ 0 (for j = 1, 2, …, n)
where Σ= Greek letter capital sigma, which means “the sum of”.
The above problem is formulated in a more general form:
Minimize Z= 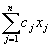 Subject to
Subject to
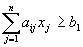 (for i = 1, 2, …, m)
and xj ≥ 0 (for j = 1, 2, …, n)
The basic difference between the maximization and the minimization problems in linear programming is found in the signs of the inequalities of the side constraints. The side constraints are expressed by the “less than or equal to” signs (i.e., ≤) in the maximization problem; whereas those of the minimization problem are expressed by the “greater than or equal to” signs (i.e. ≥)[1].
(for i = 1, 2, …, m)
and xj ≥ 0 (for j = 1, 2, …, n)
The basic difference between the maximization and the minimization problems in linear programming is found in the signs of the inequalities of the side constraints. The side constraints are expressed by the “less than or equal to” signs (i.e., ≤) in the maximization problem; whereas those of the minimization problem are expressed by the “greater than or equal to” signs (i.e. ≥)[1].
 may be drawn by the line MM in Fig. 2-4. If the entire electronic components are used for the production of x1, 120 units of x1 can be produced. Similarly, if all the available components are used for the production of x2, 100 units of x2 can be produced. The line MM is drawn by connecting these two extreme points. Any point on the line MM indicates a different production program with full utilization of available electronic components. For example, at the point M1, the production combination of 30 units of x1 and 75 units of x2 is possible; at the point M2, 60 units of x1 and units of x2; at the point M3, 84 units of x1 and 30 units of x2. All these points lie on the straight line MM, because they indicate different production programs of x1 and x2 with full utilization of available electronic components. A different product combination is also possible on any points to the left of the line MM, but not to the right, because of the limited availability of electronic components.
may be drawn by the line MM in Fig. 2-4. If the entire electronic components are used for the production of x1, 120 units of x1 can be produced. Similarly, if all the available components are used for the production of x2, 100 units of x2 can be produced. The line MM is drawn by connecting these two extreme points. Any point on the line MM indicates a different production program with full utilization of available electronic components. For example, at the point M1, the production combination of 30 units of x1 and 75 units of x2 is possible; at the point M2, 60 units of x1 and units of x2; at the point M3, 84 units of x1 and 30 units of x2. All these points lie on the straight line MM, because they indicate different production programs of x1 and x2 with full utilization of available electronic components. A different product combination is also possible on any points to the left of the line MM, but not to the right, because of the limited availability of electronic components.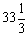 ) = 6,666
) = 6,666 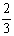
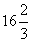 ,27
,27  ) D (0,50)
) D (0,50)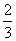 ) + 3,500 (27
) + 3,500 (27